数据结构：堆的实现

原创 已于 2024-05-18 17:46:17 修改 · 968 阅读 · 14 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #c语言

于 2024-05-18 17:45:47 首次发布

目录

什么是堆？

堆的类型

   1、大堆

        2、小堆

堆的实现

        代码思路：

        代码实现：

        1、堆的创建、初始化和销毁

        2、 堆的插入

         3、堆的删除

        4、取堆顶的数据

        5、取堆的数据个数

        6、判空

什么是堆？

        堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。

   堆的性质：

  • 堆中某个结点的值总是不大于或不小于其父结点的值；
  • 堆总是一棵完全二叉树。

（更详细的定义->堆（数据结构）_百度百科）  

堆的类型

   1、大堆

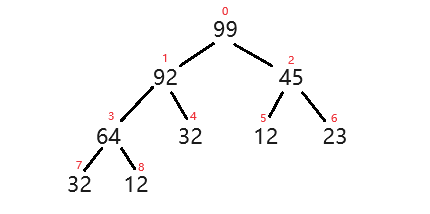
        这是一个大堆，我们可以发现它们数值的大小总是小于上一级的，并且大于下一级的，与同级的无关；同时它们的上一级是（自身的位置 - 1）/ 2，且自身的下一级为（自身*2+1）或者（自身*2+2）。

        2、小堆

        

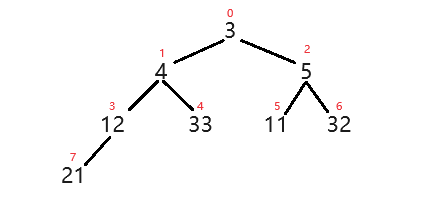
         这是一个小堆，我们可以发现它们数值的大小总是大于上一级的，并且小于下一级的，且与同级的无关；同时它们的上一级是（自身的位置 - 1）/ 2，且自身的下一级为（自身*2+1）或者（自身*2+2）。

堆的实现

        代码思路：

        （我们以上面的大堆理论模型例子）我们可以发现，（父级 * 2）+  1 和（父级 * 2）  + 2是它的左孩子和右孩子，且（孩子 - 1）/ 2，所以我们可以使用柔性数组来实现堆。在理论上，堆是像树一样分布着，但实际上，它在计算机里是紧密挨着排布的。

        当我们要插入一个数的时候，先插入柔性数组里，然后再比较父子级的大小关系，从而来调整堆。

        当我们要删除一个数据的时候，先交换柔性数组里的首位数据，然后再进行调整。

        代码实现：

        （以建立大堆为例）

//设计柔性数组
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

//交换数据
void Swap(HPDataType* a, HPDataType* b)
{
	HPDataType tmp = *a;
	*a = *b;
	*b = tmp;
}

//堆的初始化
void HeapInit(Heap* php)
{
	assert(php);

	php->_a = NULL;
	php->_size = php->_capacity = 0;
}

// 堆的销毁
void HeapDestory(Heap* php)
{
	assert(php);

	free(php->_a);
	php->_a = NULL;
	php->_size = php->_capacity = 0;
}

//向上调整
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

// 堆的插入
void HeapPush(Heap* php, HPDataType x)
{
	assert(php);

	if (php->_capacity == php->_size)
	{
		int capacity = php->_capacity == 0 ? 4 : php->_capacity * 2;
		HPDataType* new = (HPDataType*)realloc(php->_a,sizeof(HPDataType) * capacity);
		if (new == NULL)
		{
			perror("HeapPush::() malloc fail");
			return;
		}
		php->_capacity = capacity;
		php->_a = new;
	}

	php->_a[php->_size] = x;
	php->_size++;
	AdjustUp(php->_a, php->_size - 1);
}

//向下调整
void AdjustDown(HPDataType* a, int parent, int n)
{
	assert(a);
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

// 堆的删除
void HeapPop(Heap* php)
{
	assert(php);
	assert(php->_size > 0);

	php->_size--;
	Swap(&php->_a[0], &php->_a[php->_size]);

	AdjustDown(php->_a, 0, php->_size);
}

// 取堆顶的数据
HPDataType HeapTop(Heap* php)
{
	assert(php);

	return php->_a[0];
}

// 堆的数据个数
int HeapSize(Heap* php)
{
	assert(php);

	return php->_size;
}

// 堆的判空
int HeapEmpty(Heap* php)
{
	assert(php);

	return php->_size == 0;
}

        1、堆的创建、初始化和销毁

        当_size和_capacity是为了以后的扩容。

//设计柔性数组
typedef int HPDataType;//方便以后实现不同需求的堆
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

//堆的初始化
void HeapInit(Heap* php)
{
	assert(php);

	php->_a = NULL;
	php->_size = php->_capacity = 0;
}

// 堆的销毁
void HeapDestory(Heap* php)
{
	assert(php);

	free(php->_a);
	php->_a = NULL;
	php->_size = php->_capacity = 0;
}

        2、 堆的插入

        每当我们插入一个数据，首先我们要对其柔性数组判断它是否还有空间，若空间不足就扩容，反之，则直接插入。

        最重要的来了，当插入完数据后，我们要对堆进行调整，这里我使用的是向上调整，根据我们上面父子级的关系可以先比较它们之间的大小是否要交换数据，若交换了，记得要将孩子到父亲的位置，父亲要调到它父亲的位置，继续比较，直至孩子到根。

//交换数据
void Swap(HPDataType* a, HPDataType* b)
{
	HPDataType tmp = *a;
	*a = *b;
	*b = tmp;
}

//向上调整
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

// 堆的插入
void HeapPush(Heap* php, HPDataType x)
{
	assert(php);
    //当_size == _capacity相等的时候就扩容
	if (php->_capacity == php->_size)
	{
		int capacity = php->_capacity == 0 ? 4 : php->_capacity * 2;
		HPDataType* new = (HPDataType*)realloc(php->_a,sizeof(HPDataType) * capacity);
		if (new == NULL)
		{
			perror("HeapPush::() malloc fail");
			return;
		}
		php->_capacity = capacity;
		php->_a = new;
	}
    //插入数据
	php->_a[php->_size] = x;
	php->_size++;
    //向上调整
	AdjustUp(php->_a, php->_size - 1);
}

         3、堆的删除

        当我们要删除数据的时候，不是删除尾的数据，删除堆的尾是没有什么意义的，要删除堆的根的数据。

        要删除堆的根的数据。首先，我们要交换头尾的数据，然后再调整堆。因为我们要删除堆的时候，已经形成了堆，我们只需要将根的数据与它的子级计较即可。

//交换数据
void Swap(HPDataType* a, HPDataType* b)
{
	HPDataType tmp = *a;
	*a = *b;
	*b = tmp;
}

//向下调整
void AdjustDown(HPDataType* a, int parent, int n)
{
	assert(a);
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

// 堆的删除
void HeapPop(Heap* php)
{
	assert(php);
	assert(php->_size > 0);

	php->_size--;
	Swap(&php->_a[0], &php->_a[php->_size]);

	AdjustDown(php->_a, 0, php->_size);
}

        4、取堆顶的数据

        堆顶的数据就是柔性数组的第一个数据。

// 取堆顶的数据
HPDataType HeapTop(Heap* php)
{
	assert(php);

	return php->_a[0];
}

        5、取堆的数据个数

        直接返回柔性数组里的数据个数即可。


// 堆的数据个数
int HeapSize(Heap* php)
{
	assert(php);

	return php->_size;
}

        6、判空

// 堆的判空
int HeapEmpty(Heap* php)
{
	assert(php);
    //当柔性数组没有数据的时候就为空
	return php->_size == 0;
}

什么是堆？如何区分大堆和小堆？什么是向上调整和向下调整算法？如何实现堆排序？一篇文章带你秒杀考研数据结构堆。
fanzhaokai0420的博客
07-28 3844
考研数据结构总结，例题全解，向上调整算法，向下调整算法，堆排序的原理，大堆和小堆
对于数据结构:堆的超详细保姆级解析——下（堆排序以及TOP-K问题）
最新发布
2503_92929084的博客
11-09 3989
本文深入解析了堆排序和TOP-K问题的解决方案。堆排序通过构建大/小堆实现高效排序，其中方法一利用额外空间（O(N)），方法二则原地排序（O(1)）。重点分析了向下调整算法（O(N)）比向上调整（O(NlogN)）更优的时间复杂度。针对TOP-K问题，提出用堆作为筛选器：前K大建小堆，前K小建大堆，仅需O(K)空间即可处理海量数据。文章通过数学推导、代码示例和分步图解，帮助读者理解堆的核心思想与应用场景，强调算法设计中效率与场景的平衡，为后续学习更复杂的数据结构打下基础。
堆实现
stay hungry,stay foolish
12-21 720
/** @file heap.c * @brief 堆，默认为小根堆，即堆顶为最小. * @author soulmachine@gmail.com */ #include /* for malloc() */ #include /* for memcpy() */ typedef int heap_elem_t; // 元素的类型 /** * @struct * @brief 堆的结构体 5
【数据结构】堆的实现（简单易懂，超级详细！！！）
m0_65679465的博客
11-25 6766
堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。本文从堆的概念和规律，到堆的实现，向下调整算法，建堆，向上调整算法等等，详细讲解，图文并茂！
堆的实现
qq_45189707的博客
03-03 221
堆的性质 1.堆中某个节点的值总是不大于或不小于其父亲节点的值； 2.堆总是一颗完全二叉树。 堆的实现 tree.h #define _CRT_SECURE_NO_WARNINGS 1 #pragma once #include <stdio.h> #include <stdlib.h> #include <string.h> #include <asse...
精选资源
数据结构：常见数据结构的 MATLAB 实现，包括树、哈希表、堆和列表-matlab开发
06-01
该包包含以下常见数据结构的基于 MATALB 类的实现： 1) 数组2) 二叉搜索树3) 哈希表4) 堆5) 列表6) 队列7) 红黑树8) 堆栈 代码的编写方式使其可以轻松翻译成其他语言。 大多数方法取自规范算法文本： 算法导论...
数据结构：堆（建堆和堆排序的python实现）
Winnie_boy的博客
05-26 1034
前言 这次我首先告诉大家堆的应用领域：TopK问题 、堆排序 、优先队列实现等 为什么这次要先告诉大家，因为这次希望先思考和结合下你们刷题或者面试的过程中，是否实现和解决过上述问题，也许不是用堆的原理解决的，但都可以更快的加深你对堆这一概念的理解，那废话不多说，我们开始吧 堆 **堆栈：**这两个词虽然经常被放在一起说，但是其实它俩在数据结构和算法中都有不同形式的体现 栈是用数据结构来实现的一种算法：数组，链表均可 堆也是用数据结构来实现的一种算法：树，数组均可 1.堆本身是一棵完全二叉树，下图记录了完全二
数据结构 堆的实现
08-13
堆是一种特殊的数据结构，通常被用作优先队列的底层实现。在本主题中，我们将深入探讨堆的实现，特别是标准大学课程中教授的方法。 堆通常是一个完全二叉树，分为两种类型：最大堆和最小堆。在最大堆中，每个节点的...
java数据结构：顺序表+链表+栈+队+堆+二叉树+常见排序+map+set代码与板书
08-02
Java 数据结构在计算机科学和编程中起着至关重要的作用。本文将介绍顺序表、链表、栈、队列、堆、二叉树、常见排序算法、Map 和 Set 的基本概念、实现代码及其应用场景。这些数据结构和算法是编写高效程序的基础，...
一个堆实现
-_-的专栏
10-13 367
//a strong type heap. #define LEFT_CHILD_POS(x) (x #define RIGHT_CHILD_POS(x) ((x #define RIGHT_SUBLING_POS(x) (x|1) #define LEFT_SUBLING_POS(x) (x&0xFFFFFFFFE) #define PARENT_POS(x) (x>>1)
【堆】的实现
m0_58103115的博客
12-08 1002
文章目录1. ????堆的概念和结构2. ????堆向下调整法3. ????堆向上调整法4. ????堆的创建5. ????堆的插入6. ????堆的删除7. ????堆的数据个数8. ????取堆顶的数据9. ????堆的销毁0.完整代码 1. ????堆的概念和结构 堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质： 堆中某个节点的值总是不大于（大堆）或不小于（小堆）其父节点的值；2.堆总是一棵完全二叉树。 一般情况下，堆的所有元素
C语言实现数据结构：堆分配存储的串操作
"数据结构C语言版的串的堆分配存储表示与实现，涉及C语言实现的串（字符串）的数据结构，包括堆分配存储、初始化、生成、复制等操作。" 在计算机科学中，数据结构是组织和管理数据的方式，而串是数据结构中的基本...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值