HDU-2138（六倍法判断素数）

最新推荐文章于 2023-11-15 09:48:50 发布

原创最新推荐文章于 2023-11-15 09:48:50 发布 · 600 阅读

0 ·

CC 4.0 BY-SA版权

【模板】同时被 2 个专栏收录

9 篇文章

订阅专栏

【素数，同余】

6 篇文章

订阅专栏

本文介绍了一个高效的素数检测算法，并通过C++实现。该算法利用了6的倍数附近的特性来减少不必要的检查，进一步通过检查小于等于其平方根的所有可能因数来确定一个数是否为素数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

How many prime numbers

Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 22283 Accepted Submission(s): 7523

Problem Description

Give you a lot of positive integers, just to find out how many prime numbers there are.

Input

There are a lot of cases. In each case, there is an integer N representing the number of integers to find. Each integer won’t exceed 32-bit signed integer, and each of them won’t be less than 2.

Output

For each case, print the number of prime numbers you have found out.

Sample Input

32 3 4

Sample Output

2

Author

wangye

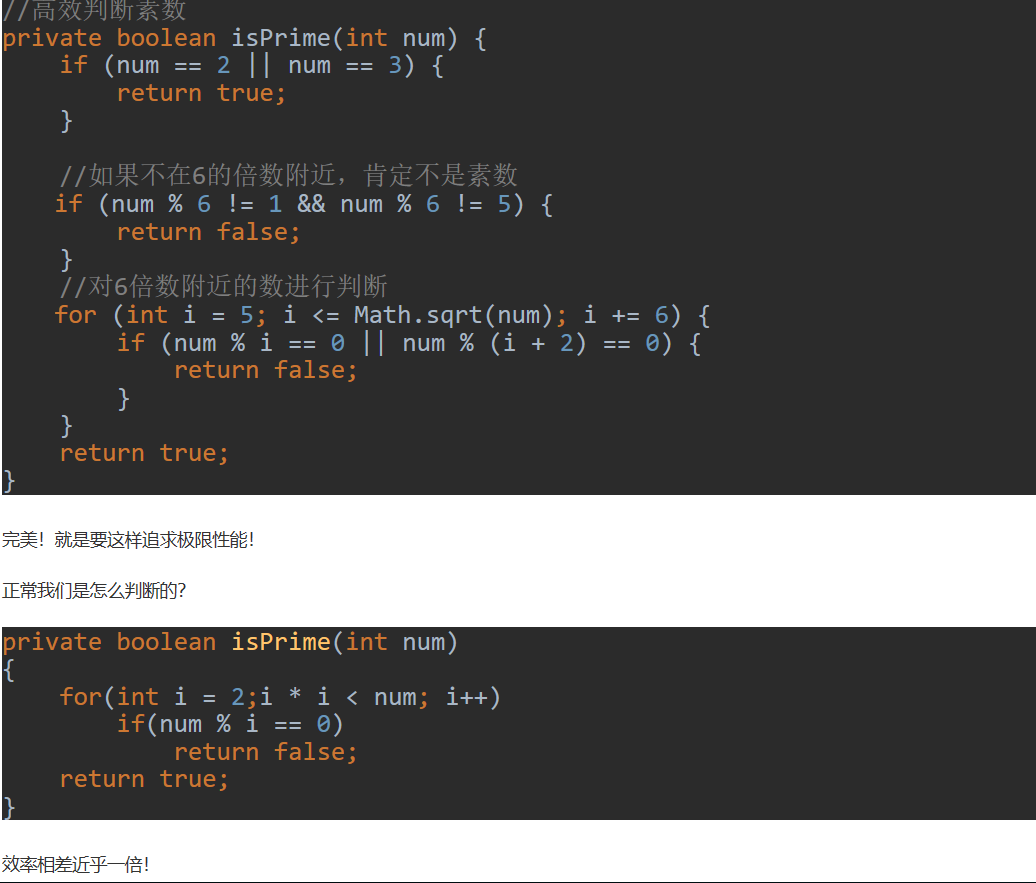
AC Code

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;

bool prime(long long x)
{
	if(x==2 || x==3) return 1;           //2,3是特例，虽然不在6的附近，但是是素数 
	if(x%6 != 1 &&  x%6 != 5) return 0; //如果不在6的倍数附近，肯定不是素数
	else							    //对6倍数附近的数进行判断
	{
		for(long long i=5; i<=sqrt(x); i=i+6) 
		{
			if(x%i==0 || x%(i+2)==0)
			{
				return 0;
				break;
			}
		}
     	return 1;
	}
}
int main()
{
	long long n;
	while(~scanf("%lld",&n))
	{
		long long x, sum = 0;
		for(long long i=1; i<=n; i++)
		{
			scanf("%lld",&x);
			if(prime(x)) sum++;
		}
		printf("%d\n",sum);
	}
	
	return 0;
}