poj1470-Closest Common Ancestors(Tarjan离线）

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form: 

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ... 

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
For example, for the following tree: 

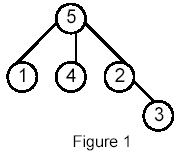
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Huge input, scanf is recommended.

 

 

题意：给了一棵树，然后q组询问，寻找他们的最近公共祖先，最后计算这些公共祖先出现了多少次。

比如2 3 的LCA是2，其它询问的LCA都是5，所以2出现了一次，5出现了5次。

 

因为输入的处理WA了好多次...

代码还要多组输入。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define eps 1e-8
#define memset(a,v) memset(a,v,sizeof(a))
using namespace std;
typedef long long int LL;
const int MAXL(1e3);
const int INF(0x7f7f7f7f);
const int mod(1e9+7);
int dir[4][2]= {{-1,0},{1,0},{0,1},{0,-1}};
struct node
{
    int to;
    int next;
} edge[MAXL+50];
int head[MAXL+50];
int father[MAXL+50];
int ans[MAXL+50];
bool vis[MAXL+50];
bool is_root[MAXL+50];
vector<int>v[MAXL+50];
int n;
int cnt;
int root;


int Find(int x)
{
    if(x!=father[x])
        father[x]=Find(father[x]);
    return father[x];
}

void Join(int x,int y)
{
    int fx=Find(x),fy=Find(y);
    if(fx!=fy)
        father[fy]=fx;
}


void LCA(int u)
{
    for(int i=head[u]; ~i; i=edge[i].next)
    {
        int v=edge[i].to;
        LCA(v);
        Join(u,v);
        vis[v]=true;

    }
    for(int i=0; i<v[u].size(); i++)
    {
        int w=v[u][i];
        if(vis[w]==true)
        {
            int lca=Find(w);
            ans[lca]++;
        }
    }
}


void add_edge(int x,int y)
{
    edge[cnt].to=y;
    edge[cnt].next=head[x];
    head[x]=cnt++;
}

void init()
{

    cnt=0;
    memset(head,-1);
    memset(vis,false);
    memset(is_root,true);
    memset(ans,0);
    for(int i=1;i<=n;i++)
        v[i].clear();
    for(int i=0; i<=n; i++)
        father[i]=i;
    for(int i=1; i<=n; i++)
    {
        int x,y;
        int num;
        scanf("%d:(%d)",&x,&num);
        for(int j=1; j<=num; j++)
        {
            int y;
            scanf("%d",&y);
            add_edge(x,y);
            is_root[y]=false;
        }
    }
    int t;
    scanf("%d",&t);
    for(int i=1; i<=t; i++)
    {
        int x,y;
        while(getchar()!='(');
        scanf("%d%d",&x,&y);
        v[x].push_back(y);
        v[y].push_back(x);
    }
    while(getchar()!=')');
    for(int i=1; i<=n; i++)
        if(is_root[i]==true)
            root=i;
}

int main()
{
    while(~scanf("%d",&n))
    {
        init();
        LCA(root);
        for(int i=1; i<=n; i++)
        {
            if(!ans[i])
                continue;
            cout<<i<<":"<<ans[i]<<endl;
        }
    }
}