题目描述:
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
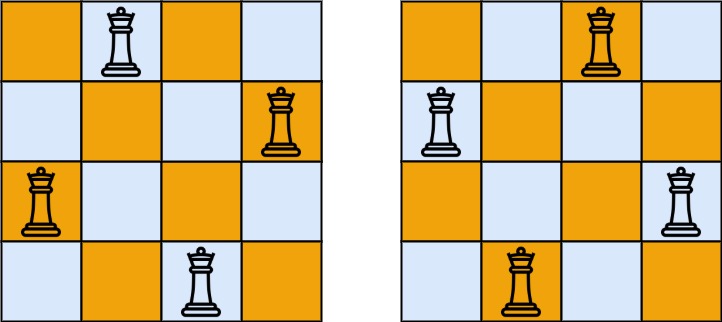
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9
我的作答:
累了。。。。。。。。
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
if not n: return [[]]
space = [['.']*n for _ in range(n)]
result = []
def is_safe(i, j):
# 检查同一列
for row in range(i):
if space[row][j] == 'Q':
return False
# 检查左上对角线
row, col = i-1, j-1
while row >=0 and col >=0:
if space[row][col] == 'Q':
return False
row -= 1
col -= 1
# 检查右上对角线
row, col = i-1, j+1
while row >=0 and col < n:
if space[row][col] == 'Q':
return False
row -= 1
col += 1
return True
def backtracking(row, count):
if count == n:
result.append([''.join(row) for row in space])
return
for col in range(n):
if is_safe(row, col):
space[row][col] = 'Q'
backtracking(row+1, count+1)
space[row][col] = '.'
backtracking(0, 0)
return result
参考:
无
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








