快速幂

2020/3/5
今天遇到一道题，n的数据范围10的18次方，一想，正好用longlong可以盛下，再仔细一看，好家伙，这个数据还是个指数，2^n次幂，我直接裂开。

借由此，我学习了快速幂的有关知识，写篇博文记一下。

看题解时看到快速幂这个名字我还不以为然，你再怎么快，2^n也不是longlong能放下的啊。但看一下快速幂的原理，再用一些《显 而 易 见》的数论知识，我不禁拍案叫绝！

快速幂，顾名思义，是一般指数运算的优化，但是快速幂函数如果增加一个参数，还有另一个作用，就是求出结果关于这个新的参数的取模！神奇不神奇？

有一个显然的数论知识先介绍一下：(a*b)%m == a*(b%m)%m
这个比较显然，举几个例子看一下就好了。

快速幂有两种方式：递归实现与非递归实现

首先看递归实现，代码很短，对照注释就能看懂：

typedef long long ll;

ll fp(ll a, ll b, ll m) {//表示a^b%m
	if (b == 0) return 1;//指数为零返回1，递归边界
	if (b & 1) {//位运算，等价于b是奇数
		return a * fp(a, b - 1, m) % m;
	}
	ll temp = fp(a, b / 2, m) % m;
	return temp * temp % m;
}//每一个算式都%m一下，反正指数就是一系列的乘法，随便加%m不会影响结果

可以看出，快速幂的复杂度就是O(logn)，相对于for循环累乘复杂度降低了不少，但是递归有一个缺陷，那就是空间占用大，所以我们通常用的不是上面这个看起来比较高级的递归算法，反而是下面的非递归算法：

typedef long long ll;

ll fp(ll a, ll b, ll m) {
	ll ans = 1;
	while (b > 0) {
		if (b & 1) ans = ans * a % m;
		a = a * a % m;
		b >>= 1;
	}
	return ans;
}

以下是数学解释（无视所有的%m）：


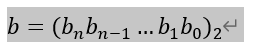
每次a自乘，b右移（位运算），结果ans，如果b该位为1则乘a，反之不管。

21/3/7改
测试发现第二段代码有bug，因为如果 b == 0 and k == 1时，返回值是1，但其实应该是0 。

修改：把函数第一行加一个判断，如果m是1的话直接返回0就行了，这样也优化了整体函数结构。

typedef long long ll;

ll fp(ll a, ll b, ll m) {
	if(m == 1) return 0;
	ll ans = 1;
	while (b > 0) {
		if (b & 1) ans = ans * a % m;
		a = a * a % m;
		b >>= 1;
	}
	return ans;
}

快速幂不仅可以用于数字的乘方运算中，也可以用于矩阵的高次幂快速运算。

我们再来回顾一下上面这段代码，如果变成矩阵乘法，有两个重点变化要注意：
ans = ans * a % m
这里的ans我们应该初始化为单位矩阵，并且乘法要变成矩阵乘法（三重循环），在三重循环的每一个单元都取一次膜，数学原理如下式

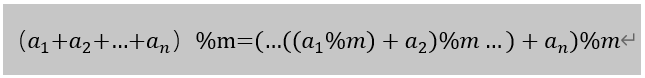
a = a * a % m这一句也是一样的，a矩阵自乘并且每步取模。

由于是矩阵，搞成二级指针可能会出现许多玄学的错误555（我决定不在VS用指针了），所以我们直接开全局变量，然后balabla

上代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;//这里的模是可以改动的，甚至可以调整为输入
int n;//n是矩阵的长宽
ll k;//k是矩阵的幂次
ll ans[110][110] = { 0 };//单位矩阵，一会要在main中初始化为单位矩阵
ll A[110][110];//同上面的a
void multi1();
void multi2();

int main()
{
	cin >> n >> k;
	for (register int i = 1; i <= n; ++i) {//忽略register（我也不太懂但据说可以变快一点）
		for (register int j = 1; j <= n; ++j) {
			cin >> A[i][j];
		}
	}
	for (int i = 1; i <= n; ++i) ans[i][i] = 1;//单位矩阵
	while (k) {//快速幂核心
		if (k & 1) multi1();
		multi2();
		k >>= 1;
	}
	for (int i = 1; i <= n; ++i) {//输出
		for (int j = 1; j <= n; ++j) {
			cout << ans[i][j] << ' ';
		}
		cout << endl;
	}
	return 0;
}

inline void multi1() {
	ll c[110][110] = { 0 };//临时储存答案的数组
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= n; ++j) {
			for (int k = 1; k <= n; ++k) {
				c[i][j] = (c[i][j] + ans[i][k] * A[k][j]) % mod;//逐步取模，注意不要用+=，如果这样的话需要再写一步（想一想为什么）
			}
		}
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= n; ++j) {
			ans[i][j] = c[i][j];//更新ans
		}
	}
}

inline void multi2() {
	ll c[110][110] = { 0 };//临时储存答案的数组
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= n; ++j) {
			for (int k = 1; k <= n; ++k) {
				c[i][j] = (c[i][j] + A[i][k] * A[k][j]) % mod;
			}
		}
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= n; ++j) {
			A[i][j] = c[i][j];//更新A
		}
	}
}