21/3/4
整个晚上都在与dfs勾心斗角,心累。。。写篇博客缓缓
dfs,又称电风扇(bushi ,全称为Depth-First-Search,即深度优先搜索,简称深优,与bfs一样,都是一种暴力的方法,时间复杂度并不比多写几个for循环少(我现在不懂剪枝别杠。但是,有一些情况,我们并不知道该写几重for循环,这时候就需要用dfs(当然一些大神真的写出了自动重数的for循环代码,文末我搬运一下供大家orz
dfs有一种基本用处——排列组合。比如一道题问我们从一堆数中选几个做加法,这就要用dfs来做组合问题。
先说比较简单的排列问题(题自洛谷
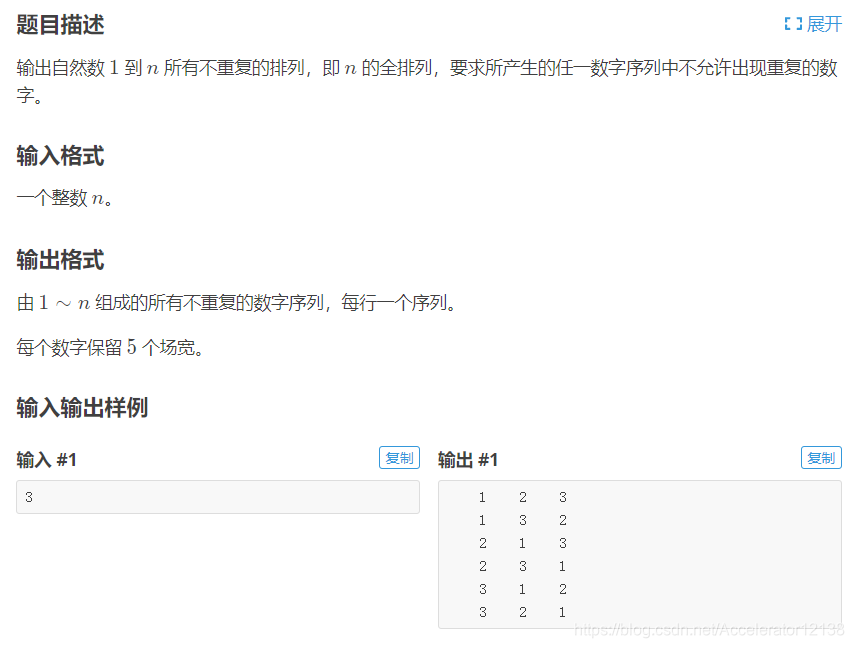
很显然要求1到n的全排列。如果只是问情况数还好点,就是n!,大不了高精一下。但是要把所有情况都列举出来,这就要电风扇了。
dfs与bfs不同,dfs是回溯算法的一种,也就是说dfs函数体内会用到dfs本身,而bfs一般不会(至少我没见过),废话不多说,上代码。
#include<bits/stdc++.h>
using namespace std;
//本代码不使用数组第零项
int a[11] = { 0 };
bool ifexist[11] = { 0 };//判定序列,判定某一个数是否已经存在过
int n;
void dfs(int x) {//这里的x可以理解为从x个位置往后的情况(此时x位置是空的),所以主函数要用dfs(1),即为从第一项往后的情况
if (x > n) {//dfs(n)已经是最后一项,赋值完成后就可以输出了
for (int i = 1; i <= n; ++i) cout << " " << a[i];//题目要求的格式
cout << endl;
return;
}
for (int i = 1; i <= n; ++i) {
if (ifexist[i] == 0) {//如果数字i在之前没有用过
a[x] = i;//这四行自行体会,无法言喻的妙处
ifexist[i] = 1;
dfs(x + 1);
ifexist[i] = 0;
}
}
return;
}
int main() {
cin >> n;
dfs(1);
}
以上是排列,如果是组合呢?另外一个很重要的扩展,上面说了1到n的全排列,但如果是任意n个数,甚至是字符,又该怎么办?
先说任意n个东西的全排列。。。hhhhh就是把上面代码“无法言喻的妙处”那一行的i改成num[i]就是了。
接下来是重头戏!1到n的组合与任意n个东西的组合。
为了少记点东西,我就不单独讲1到n的组合了,任意n个东西的组合也包含着1到n的情况啊,所以我们直接上升到任意n个东西的组合。
这里的任意n个东西,不妨就设为n个int(其他都一样),我们在定dfs函数的时候来一个第二参数,用来记录访问位置,下一次递归就把访问位置加一,保证不会有重复的(听不懂这句没关系,我自己都看不太懂,看代码就明白了)
来道例题(题自洛谷
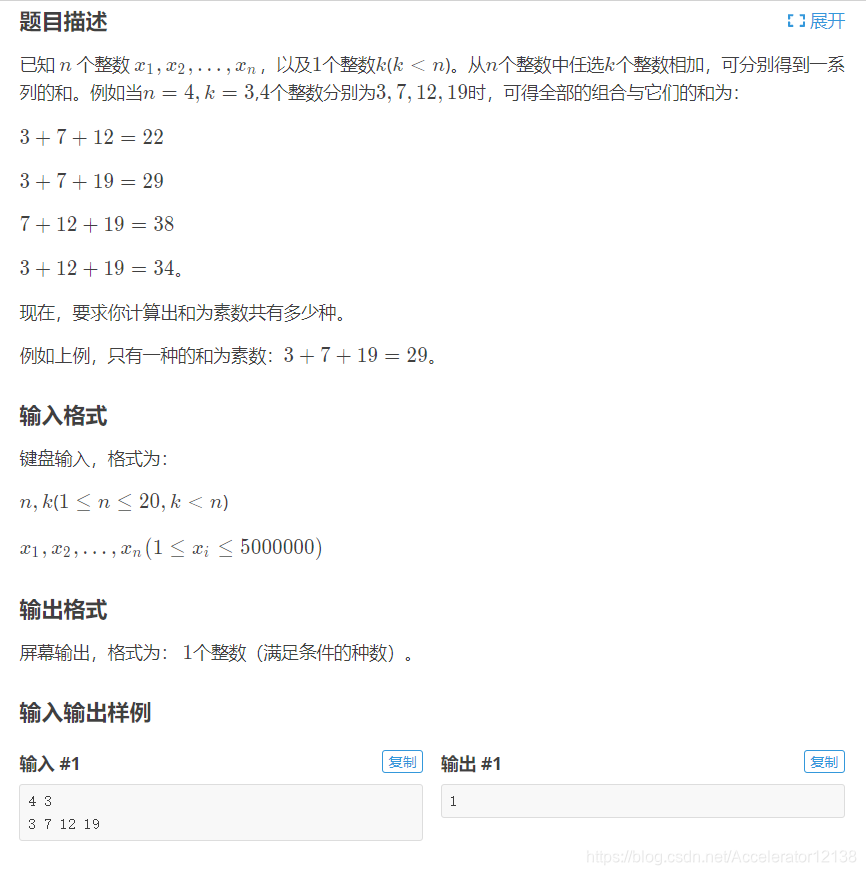
这道题就是给我们一堆数然后随机选几个做加法的,要用dfs,而且给我们的一堆数还不是1到n,是随机的一堆数。
上代码
#include<bits/stdc++.h>
using namespace std;
int num[25] = { 0 };//这是接受输入数据用的数组
int a[25] = { 0 };//这是类似于上个代码的a的a(我在说什么)
bool v[25] = { 0 };//这里的v类似于上段代码的ifexsit
int n, k;//题目定义的n和k
int sum;//用来保存加法的结果
int ans = 0;//答案,即有几种情况
void dfs(int, int);
bool ifprime(int);//判定质数函数
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; ++i) {
cin >> num[i];
}
dfs(1, 1);
cout << ans;
return 0;
}
bool ifprime(int k) {//无需多言(不会吧不会吧不会还有人不会判断质数吧)
if (k == 1) return 0;
for (int i = 2; i * i <= k; ++i) {
if (k % i == 0) return 0;
}
return 1;
}
void dfs(int x, int temp) {//妙不可言的dfs
if (x > k) {
if (ifprime(sum)) {
ans++;
}
return;
}
for (int i = temp; i <= n; ++i) {
if (v[i] == 0) {
a[x] = num[i];
sum += a[x];
v[i] = 1;
dfs(x + 1, i + 1);
sum -= a[x];
v[i] = 0;
}
}
return;
}
应用dfs做排列组合是dfs的一个很重要的用处(大概
附上洛谷大神们的打表(无限for制 妈妈问我为什么跪着看代码
#include <bits/stdc++.h>
#define ff(i) for (int i=1;i<=n;i++)
#define f(x,y) for (int y=x+1;y<=n;y++)
using namespace std;
bool zs(int x)
{
for (int i=2;i<=sqrt(x);i++)
if (x%i==0)
return 0;
return 1;
}
int n,x,a[25],b[95000001]={0},mx=-1,c=0;
int main()
{
cin>>n>>x;
for (int i=1;i<=n;i++)
cin>>a[i];
if (x==1)
{
ff(i)
{
if (zs(a[i]))
b[a[i]]++;
if (a[i]>mx)
mx=a[i];
}
}
if (x==2)
{
ff(i)
{
f(i,j)
{
int m=a[i]+a[j];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
if (x==3)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
int m=a[i]+a[j]+a[k];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
if (x==4)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
int m=a[i]+a[j]+a[k]+a[l];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
if (x==5)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
if (x==6)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
if (x==7)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
if (x==8)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
if (x==9)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
if (x==10)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
if (x==11)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==12)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==13)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
f(pp,qq)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp]+a[qq];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==14)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
f(pp,qq)
{
f(qq,rr)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp]+a[qq]+a[rr];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==15)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
f(pp,qq)
{
f(qq,rr)
{
f(rr,ss)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp]+a[qq]+a[rr]+a[ss];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==16)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
f(pp,qq)
{
f(qq,rr)
{
f(rr,ss)
{
f(ss,tt)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp]+a[qq]+a[rr]+a[ss]+a[tt];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==17)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
f(pp,qq)
{
f(qq,rr)
{
f(rr,ss)
{
f(ss,tt)
{
f(tt,uu)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp]+a[qq]+a[rr]+a[ss]+a[tt]+a[uu];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==18)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
f(pp,qq)
{
f(qq,rr)
{
f(rr,ss)
{
f(ss,tt)
{
f(tt,uu)
{
f(uu,vv)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp]+a[qq]+a[rr]+a[ss]+a[tt]+a[uu]+a[vv];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
if (x==19)
{
ff(i)
{
f(i,j)
{
f(j,k)
{
f(k,l)
{
f(l,ii)
{
f(ii,jj)
{
f(jj,kk)
{
f(kk,ll)
{
{
f(ll,mm)
{
f(mm,nn)
{
f(nn,oo)
{
f(oo,pp)
{
f(pp,qq)
{
f(qq,rr)
{
f(rr,ss)
{
f(ss,tt)
{
f(tt,uu)
{
f(uu,vv)
{
f(vv,ww)
{
int m=a[i]+a[j]+a[k]+a[l]+a[ii]+a[jj]+a[kk]+a[ll]+a[mm]+a[nn]+a[oo]+a[pp]+a[qq]+a[rr]+a[ss]+a[tt]+a[uu]+a[vv]+a[ww];
if (zs(m))
b[m]++;
if (m>mx)
mx=m;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
for (int i=1;i<=mx;i++)
{
if (b[i])
c+=b[i];
}
cout<<c;
return 0;
}





















 431
431












