K-Means聚类算法

介绍
K-Means称为聚类算法。聚类是将一个数据集中在某些方面相似的数据成员进行分类的过程，聚类技术通常称为无监督学习。

核心思想
K均值聚类算法就是先随机选取K个对象作为初始聚类中心，然后计算每个对象与聚类中心之间的距离，把每个对象分配给离它最近的聚类中心。一旦所有对象都被分配了，每个聚类中心就会根据聚类中现有的对象重新计算，重复此过程，直到满足某个终止条件。一般的终止条件可以是：所有的聚类中心都不在发生变化。

代码示例

import numpy as np
import matplotlib.pyplot as plt
import  math

'''
    训练集，分成两部分，便于观察训练结果
'''
data1 = np.random.randint(0,50,size=(50,2))
data2 = np.random.randint(50,100,size=(50,2))
trainData = np.concatenate([data1,data2])

# 初始化圆心，这里分为2类
def initialize_center(t_data):
    num_1 = np.random.randint(0,50)
    num_2 = np.random.randint(0,50)

    # 确保两圆心不是同一点
    while num_1 == num_2:
        num_2 = np.random.randint(0,50)
    C1 = [t_data[num_1][0],t_data[num_1][1]]
    C2 = [t_data[num_2][0],t_data[num_2][1]]
    print("初始化的圆心C1,C2 : "+str(C1)+' '+str(C2))
    return [C1,C2]

'''
    参数说明：
        data : 训练集数据点
        C1 : 圆心一
        C2 : 圆心二
    返回标记数组
'''
def cir_distance(data,C1,C2):
    mark = []
    for i in range(0,int(data.size/2)):
        # 计算距离
        dist_1 = math.sqrt((data[i][0] - C1[0])**2 + (data[i][1] - C1[1])**2)
        dist_2 = math.sqrt((data[i][0] - C2[0])**2 + (data[i][1] - C2[1])**2)
        if dist_1 < dist_2:
            mark.append(1)          # 标记为1类别
        else:
            mark.append(2)          # 标记为2类别
    return np.array(mark)

'''
    函数功能：更新圆心
    参数说明：
        data : 训练集数据
        mark : 标记数据
    返回更新后的圆心,list类型
'''
def get_new_center(data,mark):
    mark_1 = data[mark == 1]
    mark_2 = data[mark == 2]
    #print(mark_1)
    sum_x1,sum_y1,sum_x2,sum_y2 = 0,0,0,0
    for i in range(0,int(mark_1.size/2)):
        sum_x1 = sum_x1 + mark_1[i][0]
        sum_y1 = sum_y1 + mark_1[i][1]
    C1 = [int(sum_x1 / (mark_1.size / 2)),int(sum_y1 / (mark_1.size / 2))]
    for j in range(0,int(mark_2.size/2)):
        sum_x2 = sum_x2 + mark_2[j][0]
        sum_y2 = sum_y2 + mark_2[j][0]
    C2 = [int(sum_x2 / (mark_2.size / 2)), int(sum_y2 / (mark_2.size / 2))]
    return [C1,C2]


'''
    画图：训练集的图形，训练后两圆心的位置，
'''
def plot(t_data,mark,C1,C2,i):
    red = t_data[mark == 1]
    blue = t_data[mark == 2]
    plt.scatter(red[:,0],red[:,1],10,'r')
    plt.scatter(blue[:,0],blue[:,1],10,'b')
    plt.scatter(C1[0],C1[1],100,'r','X')
    plt.scatter(C2[0],C2[1],100,'b','X')
    plt.title(" train " + str(i))
    plt.show()

'''
    分类函数
    参数说明：
        t_data : 训练集数据
        C1、C2 : 圆心
        N : 迭代次数
'''
def classify(t_data,C1,C2,N):

    # 迭代N次
    for i in range(0,N):
        mark = cir_distance(t_data,C1,C2)           # 返回标记数组
        last_C1,last_C2 = C1,C2
        C1,C2 = get_new_center(t_data,mark)                # 更新圆心
        print('训练'+str(i+1)+'次后的圆心'+str(C1)+' '+str(C2))
        if(last_C1 == C1 and last_C2 == C2):        # 如果聚类中心没有发生变化，终止聚类
            print('共训练'+str(i+1)+'次')
            break
        else:
            plot(t_data, mark, C1, C2, i)

# 主函数
def main():
    C1, C2 = initialize_center(trainData)       # 初始化圆心
    classify(trainData, C1, C2, 5)

if __name__ == '__main__':
    main()

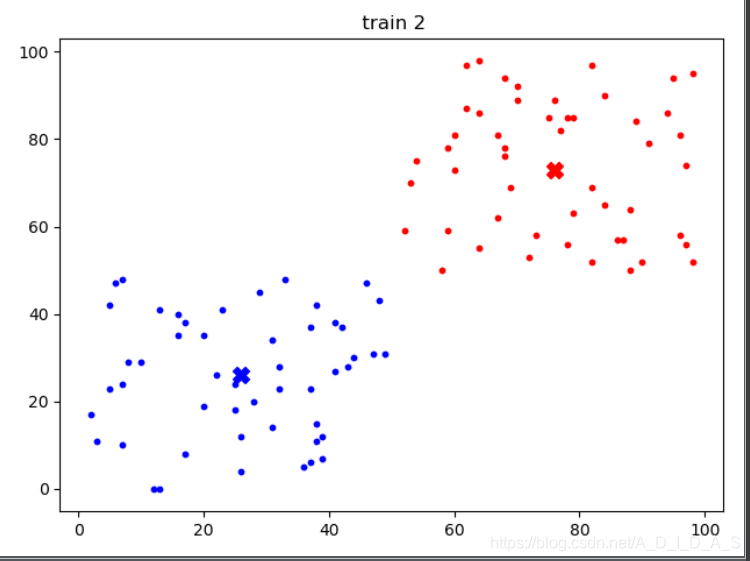
运行结果
这张图就是最终聚类的结果了，所有的圆点代表聚类对象，X代表聚类中心。

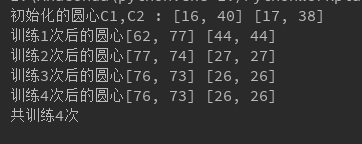
这张图显示了聚类过程中聚类中心位置的变化情况。