深度优先搜索及java实现:https://blog.youkuaiyun.com/ASN_forever/article/details/80993836
广度优先搜索
广度优先搜索是除深度优先搜索之外,对图进行搜索时采用的另一种基本算法。
广度优先搜索算法的思想
广度优先搜索使用队列进行操作。首先选定一个顶点作为起始顶点,将其放到队尾(此时也是队首)作为当前顶点,并做标记表示已读,然后寻找当前顶点(队首位置的顶点)的所有未被标记的邻接顶点,如果有,则依次插入队尾并将其标记为已读,然后将队首顶点弹出,以新的队首顶点为当前顶点,并寻找其所有未被标记的邻接顶点,然后依次插入队尾并标记已读,查找完当前顶点之后将其弹出,继续对新对手顶点进行上述操作,如此循环迭代,直到队列为空。
主要代码
public void bfs(){
vb_arr[0].isRead = true;
showVertex(0);
vq.push(vb_arr[0]);//将起始顶点插入到队尾
int v2;//用来记录与队首顶点邻接的未访问顶点所处数组下标
while(!vq.isAmpty()){//当队列不空时
int v1 = vq.pop();
while((v2 = findAdjUnvisitedVertex(v1))!=-1){//找到未访问的邻接顶点后,将其标记为已读,并插入到队尾
vb_arr[v2].isRead = true;
showVertex(v2);
vq.push(vb_arr[v2]);
}
}
for(int j=0;j<size;j++){
vb_arr[j].isRead = false;
}
} //寻找当前顶点所邻接的未被访问的顶点的数组下标
public int findAdjUnvisitedVertex(int i){
for(int j=0;j<size;j++){
if(adjMatrix[i][j] == 1&&vb_arr[j].isRead == false){
vb_arr[j].isRead = true;
return j;
}
}
return -1;
}完整java实现
public class BFSGraph {
public static void main(String[] args) {
GraphBFS gb = new GraphBFS(5);
gb.addVertex('A');
gb.addVertex('B');
gb.addVertex('C');
gb.addVertex('D');
gb.addVertex('E');
gb.addVertex('F');
gb.addEdge(0, 1);
gb.addEdge(1, 2);
gb.addEdge(0, 3);
gb.addEdge(3, 4);
gb.showAdjMatrix();
gb.bfs();
}
}
class VertexBFS{
private char elem;
public boolean isRead;
public int index;
public VertexBFS(char e){
elem = e;
isRead = false;
index = 0;
}
public char getElem(){
return elem;
}
}
class GraphBFS{
private int size;
private int[][] adjMatrix;
private VertexBFS[] vb_arr;
private int count;
private VertexQueue vq;
public GraphBFS(int size){
this.size = size;
adjMatrix = new int[size][size];
vb_arr = new VertexBFS[size];
vq = new VertexQueue(size);
count = 0;
for(int i=0;i<size;i++){
for(int j=0;j<size;j++){
adjMatrix[i][j] = 0;
}
}
}
public void addVertex(char e){
if(count<size){
VertexBFS vb = new VertexBFS(e);
vb.index = count;
vb_arr[count++] = vb;
}else{
System.out.println("顶点已满!!!");
}
}
public void addEdge(int from,int to){
adjMatrix[from][to] = 1;
adjMatrix[to][from] = 1;
}
public void showVertex(int v){
System.out.print(vb_arr[v].getElem());
}
public void bfs(){
vb_arr[0].isRead = true;
showVertex(0);
vq.push(vb_arr[0]);//将起始顶点插入到队首
int v2;//用来记录与队首顶点邻接的未访问顶点所处数组下标
while(!vq.isAmpty()){//当队列不空时
int v1 = vq.pop();
while((v2 = findAdjUnvisitedVertex(v1))!=-1){
vb_arr[v2].isRead = true;
showVertex(v2);
vq.push(vb_arr[v2]);
}
}
for(int j=0;j<size;j++){
vb_arr[j].isRead = false;
}
}
public int findAdjUnvisitedVertex(int i){
for(int j=0;j<size;j++){
if(adjMatrix[i][j] == 1&&vb_arr[j].isRead == false){
vb_arr[j].isRead = true;
return j;
}
}
return -1;
}
public void showAdjMatrix(){
for(int i=0;i<size;i++){
for(int j=0;j<size;j++){
System.out.print(adjMatrix[i][j]+" ");
}
System.out.println();
}
}
}
class VertexQueue{
private int head;
private int tail;
private int count;
private int queueSize;
private VertexBFS[] VertexQueue_Arr;
public VertexQueue(int size){
count = 0;
head = 0;
tail = -1;
this.queueSize = size;
VertexQueue_Arr = new VertexBFS[queueSize];
}
public void push(VertexBFS vb){
if(!isFull()&&tail<queueSize-1){
VertexQueue_Arr[++tail] = vb;
count++;
}else if(!isFull()&&tail==queueSize-1){
tail = -1;
VertexQueue_Arr[++tail] = vb;
count++;
}else{
System.out.println("队列已满!!!");
}
}
//返回队首元素所处数组的下标
public int pop(){
if(!isAmpty()){
int v = head;
if(head<queueSize){
head++;
count--;
return VertexQueue_Arr[v].index;
}else{
head = 0;
v = head++;
count--;
return VertexQueue_Arr[v].index;
}
}else{
return -1;//队列已空时,返回-1
}
}
public boolean isFull(){
if(count == queueSize){
return true;
}else{
return false;
}
}
public boolean isAmpty(){
if(count == 0){
return true;
}else{
return false;
}
}
}
运行结果
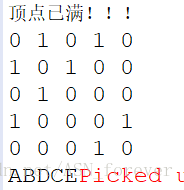








 本文详细介绍了广度优先搜索(BFS)算法的基本思想及其实现过程,通过Java代码展示了如何利用队列来遍历图中所有顶点,并提供了一个完整的示例程序,包括创建图、添加顶点和边、显示邻接矩阵以及执行BFS搜索。
本文详细介绍了广度优先搜索(BFS)算法的基本思想及其实现过程,通过Java代码展示了如何利用队列来遍历图中所有顶点,并提供了一个完整的示例程序,包括创建图、添加顶点和边、显示邻接矩阵以及执行BFS搜索。
















 624
624

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








