点分治之砍树大师

算法世界里，“分治”几乎是最经典的套路：把一个大问题拆成若干规模较小的子问题，递归解决，再把答案拼接。归并排序、快速幂，都是这样耳熟能详的例子。

数组有天然的“中点”，可以左右对半分；而无根树由节点与边连接，我们也可以选择一个节点，将树分为多个部分分治，这就叫做“点分治”。

不过，树没有一个显眼的“中间位置”。如果随便选择一个点砍掉，得到的子树大小可能极不均衡，递归效率就会大打折扣。这时，就需要一个“树上的中点”——它能保证我们每次分裂后，剩下的子树都不会太大。这个“中点”，正是重心（centroid）。

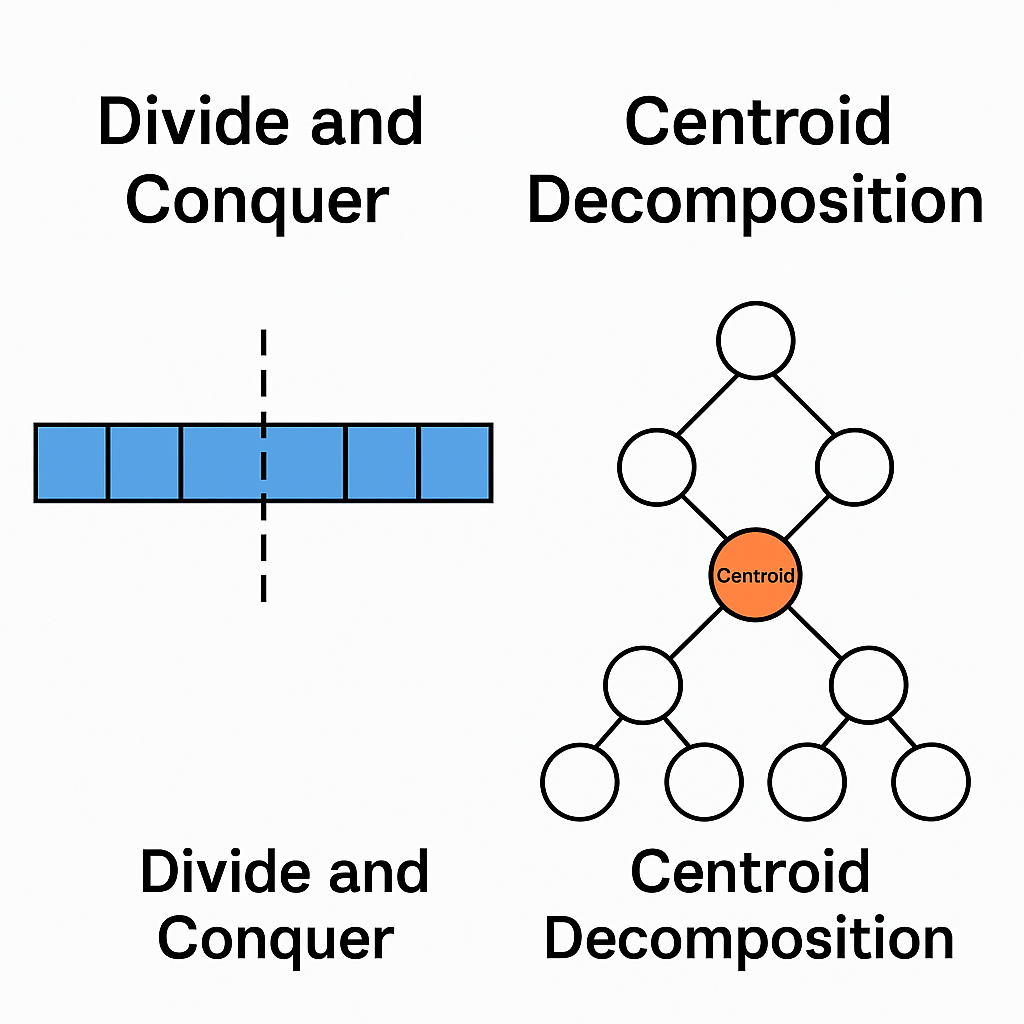
于是我们就得到了“点分治”——在树上实现分治的一种方式。核心套路是：

1. 找出树的重心。
2. 处理所有“经过重心”的答案。
3. 删除重心，递归处理每个子树。

每一步看似简单，合在一起就是一个强大的框架。

点分治的思想与重心

我们来看一个需要点分治解决的经典问题：

给定一棵 无根带权树（边权为正整数），有 �M 个询问，每个询问给出一个整数 �k，问树上有多少对点 {�,�}{u,v} 满足 距离(u, v) = k。

总的来说，点分治用分治的方法来统计路径，他的思想是：

• 选一个点作为根节点。

• 这样一来，所有路径要么两端来自两个子树并经过根节点（一端刚好就在根节点的也可以算作这个情况），要么两端都在同一个子树内，那么它没有经过根节点而完整地落在某个子树里，这就交给下一层递归去处理。

• 只处理前一种情况，然后我们递归处理每一个子树，后一种情况最终一定在某个子树里被统计到。这样，每一条路径在整个递归中只会被统计一次，不会重复，不会漏掉。

为什么要经过重心？

重心的定义：如果在无根树中选择某个节点以他为根，使得所有子树大小的最大值达到最小，那么这个点就是树的重心。重心可能不唯一，但一定存在。重心就像是树的“平衡点”，它让树的分治递归变得可行且优雅，根据定义每个子树至多是原树的一半。

每层递归都会处理一棵规模为 �N 的树，工作量是 �(�)O(N)。重心的性质保证子树最大规模 ≤ N/2，所以树的规模会对半缩小。递归深度约 �(log⁡�)O(logN)。总体复杂度就是 �(�log⁡�)O(NlogN)。

简单来说，每一次迭代都选取中心为根节点，才能保证子树规模快速减小。

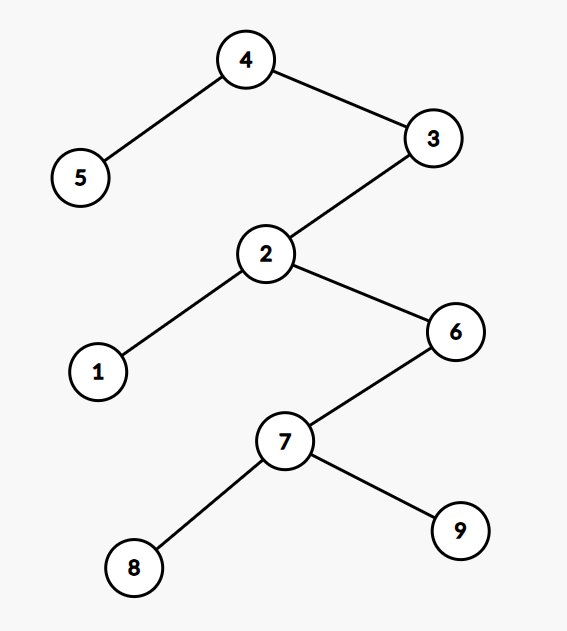
（这个无根树的重心是 2，此时最大子树大小为 4 达到最小，子树之间最大小均衡）

标准流程

1. 找重心：DFS 统计子树大小，选出“最大子树最小”的点作为重心。
2. 收集信息：从重心出发，DFS 收集到各子树的路径信息。
3. 合并答案：用数据结构（桶、哈希、bitset……）处理跨子树的路径组合。
4. 递归下去：删除重心，在子树里继续重复上面的过程。注意，新的子树要重新找他自己的重心而不是原重心的子节点。

这四步就是点分治的主干骨架。不同问题，只是在第 2、3 步处理信息的方式不一样。

典型应用：树上距离 = k 的点对计数

回到上文经典问题。朴素做法枚举点对或者暴力搜索都是平方起步，肯定不行。点分治可以 �(�log⁡�)O(NlogN) 高效解决问题。

用点分治怎么做？

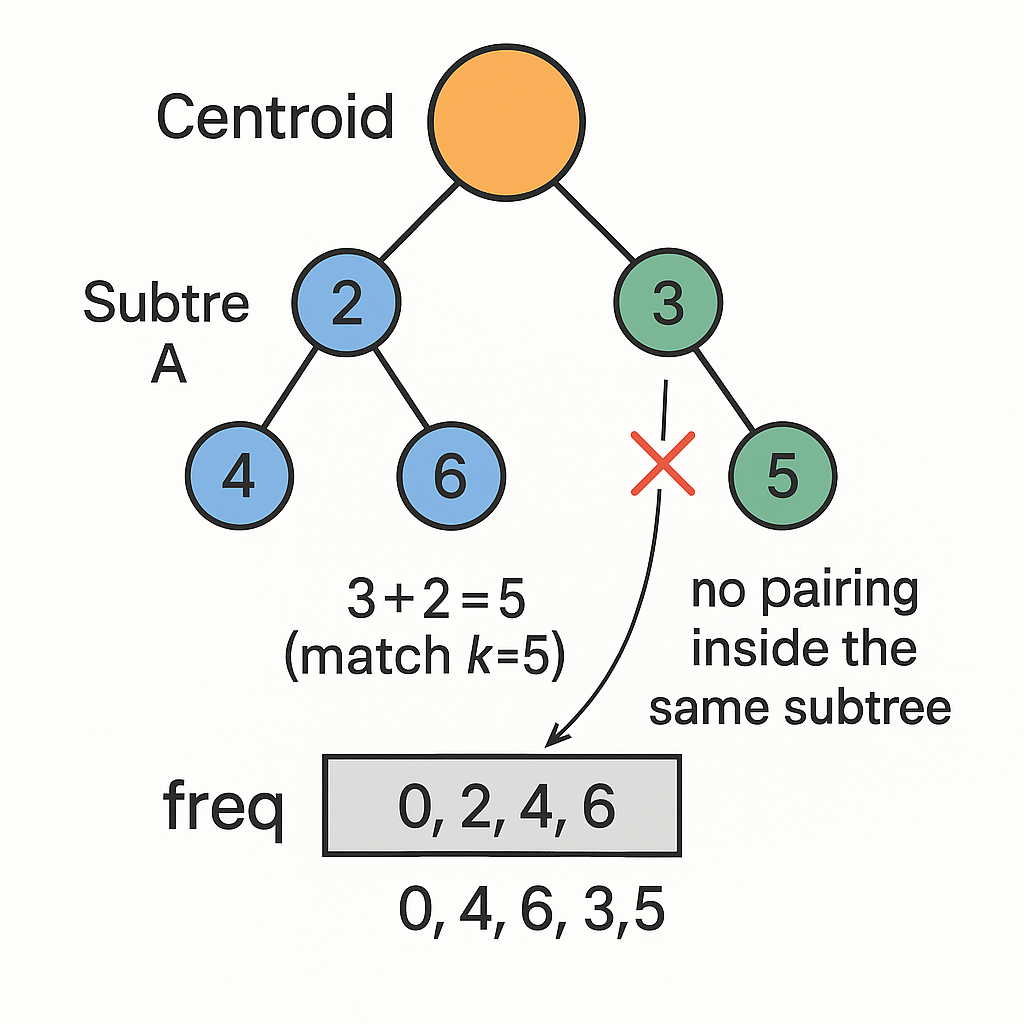
在当前重心 �c，考虑所有经过 �c 的路径。这些路径可以拆成“两段”：dist(u,c) + dist(v,c)，我们只要在不同子树之间做“配对”即可。

1. 以重心为根：从重心出发，DFS 子树，收集 dist(c, x)。

2. 配对查询：设当前子树的距离集合为 D_sub，全局已有距离集合为 freq（来自之前处理过的子树）。

   • 对每个 �∈����d∈Dsub​，对每个询问 �k，若 freq[k - d] > 0，则说明存在路径 (x, y) 距离为 �k。

3. 更新集合：处理完配对后，把 D_sub 的元素加入 freq，供后面子树使用。

4. 递归：删去重心，继续对子树点分治。

图的存储

我们用邻接表保存树：

	struct Edge {
	int to, w;
	};
	vector<vector<Edge>> g; // g[u] 存储节点 u 的所有邻边

---

重心查找

重心 = 删除后，剩余子树最大规模最小的点。

	int n;
	vector<int> sz, max_sub;
	vector<bool> vis;
	int find_centroid(int u, int fa, int tot, int &best, int &root) {
	sz[u] = 1;
	max_sub[u] = 0;
	for (auto [v, w] : g[u]) {
	if (v == fa || vis[v]) continue;
	find_centroid(v, u, tot, best, root);
	sz[u] += sz[v];
	max_sub[u] = max(max_sub[u], sz[v]);
	}
	max_sub[u] = max(max_sub[u], tot - sz[u]);
	if (max_sub[u] < best) {
	best = max_sub[u];
	root = u;
	}
	return root;
	}

---

收集距离（getDis）

DFS 收集从重心出发的所有距离。

	void get_dist(int u, int fa, int d, vector<int> &dis) {
	dis.push_back(d);
	for (auto [v, w] : g[u]) {
	if (v == fa || vis[v]) continue;
	get_dist(v, u, d + w, dis);
	}
	}

---

点分治

• 用一个哈希表/数组来保存 freq（已有子树的距离）。
• 先查后加 避免同子树内重复配对。

	unordered_map<int,int> freq; // 距离频次数组
	vector<int> ks; // 询问集合
	vector<long long> ans; // 每个询问的答案
	void solve_centroid(int u, int tot) {
	// 1. 找重心
	int best = 1e9, root = -1;
	find_centroid(u, -1, tot, best, root);
	u = root;
	vis[u] = true;
	// 2. 处理经过重心的路径
	freq.clear();
	freq[0] = 1; // 重心自身到重心的距离为 0
	for (auto [v, w] : g[u]) {
	if (vis[v]) continue;
	vector<int> dis;
	get_dist(v, u, w, dis);
	// 查询阶段（先查）
	for (int d : dis) {
	for (int i = 0; i < (int)ks.size(); i++) {
	// 这里每一个询问就分别查询了，假定询问不多。毕竟本文主题是点分治
	int k = ks[i];
	if (freq.count(k - d)) ans[i] += freq[k - d];
	}
	}
	// 更新阶段（再加）
	for (int d : dis) freq[d]++;
	}
	// 3. 递归到子树
	for (auto [v, w] : g[u]) {
	if (!vis[v]) solve_centroid(v, sz[v] < sz[u] ? sz[v] : tot - sz[u]);
	}
	}

---

参考主函数

	int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int m;
	cin >> n >> m;
	g.assign(n+1, {});
	sz.assign(n+1, 0);
	max_sub.assign(n+1, 0);
	vis.assign(n+1, false);
	for (int i = 1; i < n; i++) {
	int u, v, w;
	cin >> u >> v >> w;
	g[u].push_back({v, w});
	g[v].push_back({u, w});
	}
	ks.resize(m);
	ans.assign(m, 0);
	for (int i = 0; i < m; i++) cin >> ks[i];
	solve_centroid(1, n);
	for (int i = 0; i < m; i++)
	cout << ans[i] << "\n";
	}

效率

点分治的复杂度经常让人觉得“魔法般的高效”。我们来直观理解一下。

• 每层递归： 每层总共处理一棵大小为 �N 的树，做的事就是找重心、收集距离、更新答案，复杂度 O(N)。
• 重心的性质：删掉重心后，剩余每个子树大小 ≤ N/2。
• 递归层数：因此子树的规模每次都对半缩小，层数就是 O(log N)。总体复杂度就是 O(N log N)。