不懂决策树算法？别怕！大白话讲清算法、实现流程与信息熵、增益的计算诀窍

1、什么是决策树算法

（1）决策树像一个猜东西的游戏流程

决策树就像是一个特别有条理的猜东西游戏。比如说，我们要猜一个人心里想的动物是什么。首先从一个最有用的线索开始猜，这个线索就像是决策树的根节点。比如第一个线索是“这个动物是生活在水里还是陆地上”。如果答案是“水里”，就顺着“水里”这个分支走下去。

然后又有新的线索，比如“这个水里的动物是有壳还是没壳”，这就像是内部节点。如果答案是“有壳”，就再顺着这个分支走。最后一直这样问问题、走分支，直到猜出这个动物到底是什么，最后猜出来的这个动物就是叶节点的答案。

（2）用决策树来做选择的过程

假设你要决定今天穿什么衣服出门。根节点可以是“天气是晴天还是雨天”。如果是晴天，分支就是“去上班还是出去玩”。要是去上班，内部节点可能是“公司有重要会议还是普通工作日”。如果是有重要会议，叶节点的答案可能就是“穿正装”。这样一步一步，通过不同的条件来做决定，这就是决策树的基本思路。

（3）决策树是怎么学会做这些决策的呢

它会看很多已经知道答案的数据。比如要判断水果是苹果还是橙子，它会看很多水果的信息，像颜色、形状这些。它会找一个最能区分苹果和橙子的特点先开始，比如先看颜色。如果红色的大部分是苹果，绿色的大部分是橙子，就先按颜色来分。然后对于红色的水果，再找下一个能区分它们的特点，可能是大小或者有没有把儿，一直这样学，最后就能很好地判断一个水果是苹果还是橙子啦。

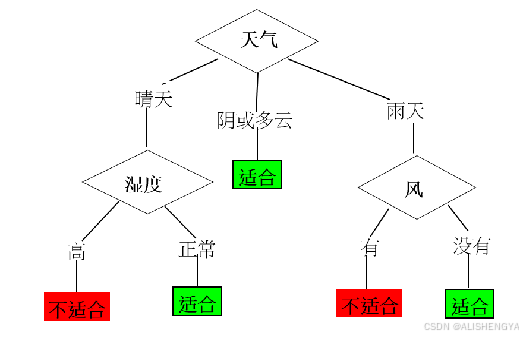
下图是判断哪些天气条件下适合外出运动的决策树模型。

2、决策树算法实现

❤在了解什么是决策树后，接下来咱们看决策树的实现原理，即如何将决策树介绍中描述的功能变成现实，有什么样的流程，如下。

决策树算法就像玩分类游戏，一点点把东西分开来判断。

（1）开头就像从一个大口袋开始

决策树算法一开始呢，就好比你有一个大口袋，里面装着所有要分类的东西，在这儿就是代表训练样本，这就是最开始的那个单独的结点。

（2）如果东西都一样，就不用再分

要是口袋里装的所有东西都属于同一类，比如说全是苹果，那这个口袋（结点）就相当于到头了，它就是个叶子结点，然后就给这个结点标上“苹果”，代表这里面都是苹果这一类东西。

（3）东西不一样就得找个好办法分开它们

可要是口袋里的东西不一样，有苹果、橙子等，那算法就得找个最厉害的办法来把它们分开，这个办法就是挑出一个最有分类能力的属性，就好像挑出一个最有用的特点。比如说按颜色来分，红色的可能是苹果，橙色的可能是橙子，那“颜色”这个特点就成了现在这个口袋（决策树当前的结点）要依据的东西。

（4）按挑好的办法把东西分到不同口袋里

按照挑出来的这个属性（像颜色），要是它有几种不同的情况（比如有红、橙、黄这几种颜色），那就根据这些不同情况来把原来口袋里的东西分别放到不同的新口袋里，每种颜色就是一个分枝，有几种颜色就有几个分枝，原来那一大口袋东西就被分成了好几个小口袋（若干子集）。

（5）每个小口袋再接着这么分下去

对于分出来的这些小口袋，算法对每个小口袋再重复上面的步骤，看看能不能再找个特点继续把小口袋里的东西再细分，就这样一直递归地往下分，慢慢地就形成了一棵像树一样的结构。而且有个规矩，要是一个特点（属性）已经在前面某个口袋（结点）那儿用过了，那后面再分这个口袋里的东西时，就不用再考虑这个特点了。

（6）什么时候就不用接着分了呢，有以下几种情况

✔小口袋里东西都一样：要是分到最后，某个小口袋里装的所有东西又都属于同一类，那这个小口袋（结点）也就变成叶子结点，就给它标上这一类的名字。

✔无法再分：要是把能用的特点（属性）都用完，实在没别的办法再接着把口袋里的东西细分，那这时候咋办呢？就看这个口袋里哪种东西最多，就按多数的那种东西来定这个口袋（结点）的类别，然后把这个口袋变成叶子结点，也可以顺便把这个口袋里各种东西分别占多少比例记下来。

✔口袋已空：要是某个口袋里根本就没东西，那就参考它上面那个大口袋（父结点）的类别来给它定个标记，然后把这个空口袋也变成叶子结点。

✔东西太少：要是某个口袋里的东西数量太少，少到低于咱们事先定好的一个数（阈值）了，那同样按这里面哪种东西最多来定个类别标记，然后把这个口袋变成叶子结点。

❤这么一步一步的，决策树算法就把东西按照不同的类别都分好。接下来，需要了解最重要的概念“最具分类能力的属性”。

3、属性选择度量

在决策树算法中，最主要的一个任务是选择一个最具分类能力的属性，如何度量一个属性是最有分类能力的?下面介绍几种属性选择的度量指标。

（1）信息增益

信息增益表示由于特征A而使得对数据D的分类的不确定性减少的程度，如下。

假设我们要对一堆水果进行分类，有苹果和橙子两种。一开始，我们只知道有一堆水果，这时候不确定性是很大的，因为我们不知道每个水果到底是苹果还是橙子。现在有一个特征是“颜色”，如果我们看颜色这个特征，发现红色的都是苹果，橙色的都是橙子。通过这个“颜色”特征来划分这堆水果后，我们就能很清楚地知道哪些是苹果，哪些是橙子了，不确定性就大大降低了。这个不确定性降低的程度就是信息增益。

❤信息增益怎么计算呢？

①信息熵计算

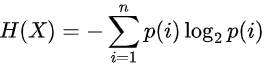
☛H（X）：表示信息熵，信息增益的计算是基于信息熵的。

☛p(i)表示类别出现的概率，n是类别数。例如，有一个装水果的盒子，里面苹果占30%，橙子占70%，那么苹果这个类别出现的概率p(苹果)=0.3，橙子这个类别出现的概率p(橙子)=0.7。这些概率反映了每种可能结果出现的相对频率。

☛

这部分是对数运算。对数函数在这里有一个特殊的作用，它使得信息熵的计算能够符合我们对不确定性的直观感受。当概率越小，log2p(i)的值越负，并且其绝对值越大。这意味着，比较少见的事件（概率小的事件）在计算信息熵时会被赋予更大的 “权重”，因为它们的出现会带来更多的不确定性。

☛求和符号表示对所有可能的类别进行求和。因为信息熵是考虑整个随机变量所有可能的结果的不确定性，所以要把每个类别对应的部分都加起来。

☛前面的负号是为了保证信息熵的值是正数。因为P(i)是概率，取值在0到1之间，log2p(i)是负数，乘以-1后就得到了正数的信息熵。

②信息增益计算

其中H（D）是未使用特征划A分数据集D时的信息熵，代表了划分前数据集的不确定性；H（D|A）是使用特征A划分数据集D后的信息熵，代表了划分后数据集的不确定性。