FHQ Treap 详解

原创

已于 2022-11-24 17:52:01 修改 · 6.2k 阅读

41 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #数据结构 #C++ #深度学习

于 2021-06-21 10:47:35 首次发布

0. 简单介绍

FHQ Treap,以下简写为fhq,是一种treap(树堆)的变体,功能比treap强大,代码比splay好写,易于理解,常数稍大.
fhq不需要通过一般平衡树的左右旋转来保持平衡,而是通过分裂split和合并merge来实现操作.
本文力求简明易懂,在看本文前最好先了解过一种平衡树的基本写法,否则代码部分有可能看不懂.

1. 前置操作

~~置渲染成一坨了~~ 现在修好了

结构

以结构体作为树的每一个节点,存储左子树和右子树的位置,权值,堆权值(用处在下面会说)和子树大小.一般子树大小用于查排名和查值.
root是树根编号,idx是点的编号,x,y,z在下面会用到.

struct Node {
   
   
    int l, r; // 左右子树编号
    int key, val;  //key权 val堆权
    int size;  //子树大小 
} tr[N];
int root, idx;
int x, y, z;

fhq和treap一样满足treap的性质,也就是既是BST,又是随机权值的堆.
至于为什么满足堆的性质的BST就能平衡,有如下定理保证:

一颗有n个不同关键字随机构建的BST的期望高度为 $l o g n$ .

随机堆的权值正是模拟了随机构建BST,所以treap是平衡的,同理fhq也平衡.

但是事实上fhq按照这种结构并不是一个标准的BST,后面我会解释.

创建节点和更新子树大小

int get_node(int key) {
   
   
    tr[++idx].key = key;
    tr[idx].val = rnd();
    tr[idx].size = 1;
    return idx;
}
void update(int p) {
   
   
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;
}

子树大小由两侧子树和根节点更新.
rnd()为随机值产生函数,需要导入random库,在开头写下如下代码:

std::mt19937 rnd(233);  //高性能随机数生成器 随机范围大概在(maxint,+maxint),233为种子,19937指该随机数循环节为2^19937

分裂 $s p l i t$

split操作按key将树由根root开始将树分为两颗x,y,其中x子树中的权值<=key,y中子树的权值>key.下面的x和y都以此为标准.
以6为分界线
split的操作如下

递归遍历左右子树
如果当前节点值<=key,则前当前节点及其左子树都可以放到x上,右子树中可能有可以放到x上的(<=key),继续递归
如果当前节点值 > key,则前当前节点及其右子树都可以放到y上,左子树中可能有可以放到y上的( > key),继续递归
若当前节点为0,说明为空,令x = y = 0,返回

注意这个操作中x和y都是引用,每一层的x和y都表示一层中的树的根节点.

//将p子树以按key拆成x和y子树,其中x中的点<=key,y中全部大于key
void split(int p, int key, int &x, int &y) {
   
   
    if (!p)
        x = y = 0;
    else {
   
   
        if (tr[p].key <= key) {
   
                  //当前节点小,放x上
            x = p;                            //x上暂时放的p子树,还要去看p的右子树
            split(tr[p].r, key, tr[p].r, y);  //去看p右子树,如果有小于key的(大于根)则应该保留在p右子树上(最后给x),否则放在y上
        } else {
   
   
            y = p;
            split(tr[p].l, key, x, tr[p].l);  //去看p左子树,如果有>=key的则应该放在p左子树上(最后给y),否则放在x上
        }
        update(p);//写在else里面,防止更新0点(否则0点size++,所有结果都不对)
    }
}

合并 $m e r g e$

merge操作按照堆权合并x,y两颗子树,合并前要保证x子树中的权值<y子树中的权值
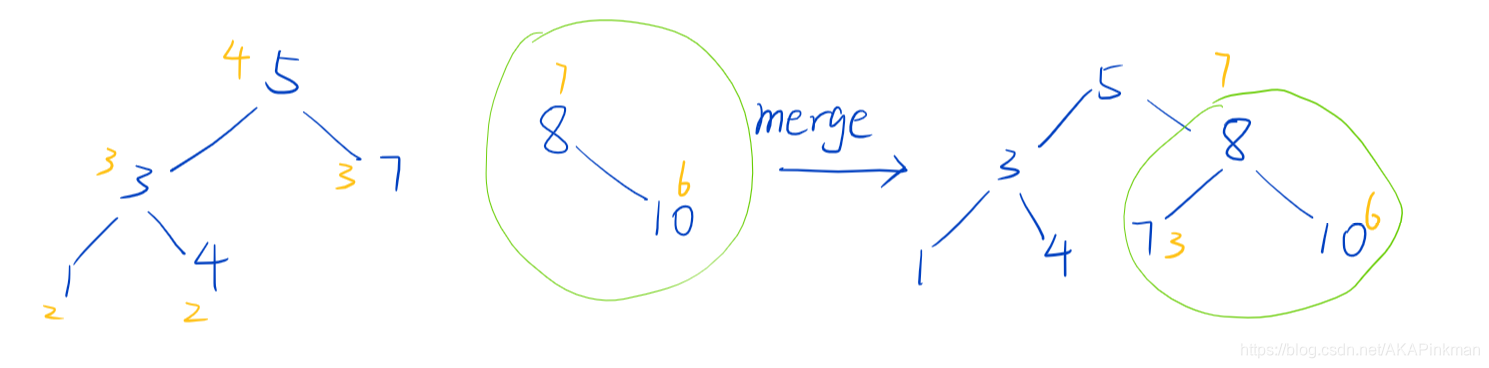
在这里插入图片描述
图中黄字为堆权,可以看到8如果直接合并在7的右侧深度会变为4,而根据堆权来看,8堆权为7,7的堆权为3,故排在7的上面,所以如此合并后树仍然平衡.

//合并x,y子树,其中x子树的值<=y子树的值
int merge(int x, int y) {
   
   
    if (!x || !y) return x + y;       //x = 0答案是y,y = 0答案是x,也就是如果有一个子树为空则返回另一个子树
    if (tr[x].va