决策树回归纯享版

目录

一、为什么进行决策树回归

二、什么是决策树回归

三、优缺点

四、决策树回归案例分析

---

一、为什么进行决策树回归

当你有一个回归问题时，决策树回归可以帮助你预测连续型的目标变量。以下是一个具体的例子来说明决策树回归的应用场景。

假设你是一家房地产公司的数据科学家，你的任务是根据房屋的特征预测其销售价格。你有一个包含诸如房屋面积、卧室数量、厨房状况等特征以及相应销售价格的训练数据集。

你可以使

用决策树回归来构建一个模型来预测房屋销售价格。下面是一个简化的例子代码：

import pandas as pd
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn import metrics

# 读取数据
data = pd.read_csv('house_data.csv')

# 提取特征和目标变量
X = data.drop('Price', axis=1)
y = data['Price']

# 拆分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建并拟合决策树回归模型
dtr = DecisionTreeRegressor(max_depth=5)
dtr.fit(X_train, y_train)

# 在训练集和测试集上进行预测
train_pred = dtr.predict(X_train)
test_pred = dtr.predict(X_test)

# 评估模型性能
train_mse = metrics.mean_squared_error(y_train, train_pred)
test_mse = metrics.mean_squared_error(y_test, test_pred)

train_r2 = metrics.r2_score(y_train, train_pred)
test_r2 = metrics.r2_score(y_test, test_pred)

在这个例子中，使用了一个训练数据集，其中包含了房屋的特征（如面积、卧室数量、厨房状况等）和对应的销售价格。从数据集中提取了特征和目标变量，并将数据集拆分为训练集和测试集。

然后，创建了一个决策树回归模型，设置了最大深度为5，并在训练集上拟合了模型。接下来，你使用训练好的模型对训练集和测试集进行预测，并计算了均方误差和决定系数等评估指标来衡量模型的性能。

通过这个例子，可以看到决策树回归模型如何利用房屋的特征来预测其销售价格。这是一个简单的示例，实际应用中可能会涉及更多的特征和数据处理步骤。

二、什么是决策树回归

1、定义：

决策树回归是一种基于树结构的非参数回归方法，用于预测连续型的目标变量。与分类任务不同，回归任务中的决策树模型通过树的叶子节点上的平均值（或其他统计量）来预测目标变量的连续值。

2、构建过程：

        1）数据准备：准备包含自变量和因变量的训练数据。

        2）特征选择：选择最优的特征作为节点分裂的依据。常用的特征选择指标包括基尼系数、信息增益、均方差等。

        3）树的构建：根据选择的特征和特征值的切分点构建树结构。根据选择的特征对样本进行切分，将样本分配到不同的节点。

        4）递归地构建子树：对于每个子节点，重复步骤2和步骤3，递归地构建子树，直到满足终止条件。

        5）叶子节点的输出：在每个叶子节点上计算目标变量的平均值（或其他统计量），作为该叶子节点的预测值。

        6）预测：利用构建好的决策树进行预测，将测试样本沿着树结构进行分类，最终得到预测值。

三、优缺点

     优点：

1. 解释性强：决策树模型的结果易于理解和解释，可以通过树的结构和节点的特征来推断决策的依据。
2. 处理非线性关系：决策树可以处理非线性关系和特征之间的复杂互动，对于非线性的问题有较好的适应性。
3. 可处理多类别特征：决策树可以处理具有多个类别的特征，不需要进行特征编码或哑变量处理。
4. 对异常值和缺失值不敏感：决策树对于异常值和缺失值相对不敏感，不需要对这些问题进行额外的处理。
5. 可用于特征选择：决策树可以通过特征的重要性排序来进行特征选择。

     缺点：

1. 容易过拟合：决策树容易生成复杂的模型，可能在训练集上过拟合，导致在测试集上性能下降。可以通过剪枝、限制树深度等方法缓解过拟合问题。
2. 不稳定性：数据的微小变化可能导致生成完全不同的决策树，这使得决策树模型在数据集上不稳定。
3. 忽略特征之间的相关性：决策树以局部最优的方式进行分裂，可能忽略特征之间的相关性，导致在某些情况下预测准确性下降。
4. 对于连续型特征处理不佳：决策树对于连续型特征的处理相对不佳，需要事先对连续型特征进行离散化处理。

四、决策树回归案例分析

设有如下数据，其中x为输入特征对应值，y为输出值：

x	1	2	3	4	5	6	7	8	9	10
y	5.56	5.7	5.91	6.4	6.8	7.05	8.9	8.7	9	9.05

(1)选择最优切分特征j与最优切分点s：

确定第一个问题，选择最优特征，本数据据中，只有一个特征，因此，最优切分特征是x。一共有10组数据，取其中位数，得到9个切分点[1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5]，损失函数定义为最小平方损失函数。

使用下列公式计算损失值：

以切分点为1.5时进行计算，当s=1.5时，将数据分为两个部分： 第一部分:(1,5.56)，第二部分:(2,5.7)、(3,5.91)、(4,6.4)…(10,9.05)。

则c1=5.56,c2=1/9(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5

所以，带入损失函数可得：

                       

以此类推，其他切分点的损失值如下表所示：

s	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
c1	5.56	5.63	5.72	5.89	6.07	6.24	6.62	6.88	7.11
c2	7.5	7.73	7.99	8.25	8.54	8.91	8.92	9.03	9.05
loss	15.72	12.08	8.36	5.78	3.91	1.93	8.01	11.73	15.74

因此可得，当s=6.5时，loss=1.93最小，所以第一个划分点s=6.5。

(2)使用选定的(j,s)划分区域并决定输出值

将数据分为两部分，分别为x<=6.5和x>=6.5的数据，并对两部分数据重复以上计算，此处省略。

最后，可得到下列决策树模型

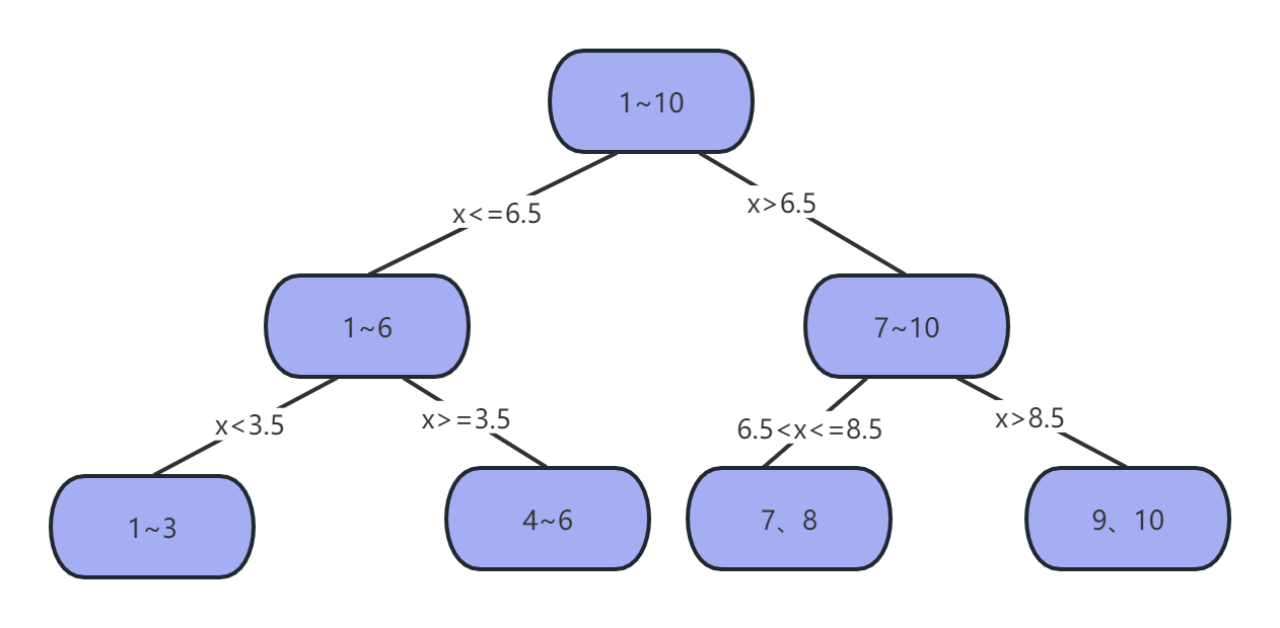
要注意的是，决策树回归并不适用于所有的回归问题。在某些情况下，其他回归算法（如线性回归、支持向量回归、神经网络等）可能更适合。