算法设计实验第二周测试题解

最新推荐文章于 2024-12-31 23:17:44 发布

原创最新推荐文章于 2024-12-31 23:17:44 发布 · 372 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法

本文探讨了如何使用递推方法解决POJ 2663 TriTiling中的矩形填充问题，以及如何通过动态规划求解2022秋_qdu_算法设计_递归分治中的整数划分。通过实例展示了如何运用递归和分治策略，结合具体算法实现和优化技巧。

POJ2663 Tri Tiling

题目链接：Tri Tiling - POJ 2663 - Virtual Judge

样例输入：

样例输出：

3
153
2131

题意：给定一个3*n的矩形快，让我们用1*2的矩形块和2*1的矩形块进行填充，求填充方案数。

我觉得这道题思维性还是挺强的，模拟了挺长时间才发现规律

设定f[n]表示填充完前n列的方案数

首先我们不难发现对于一个3*2的矩形填充方案一共是3种，那么显然f[n]中包含3*f[n-2],我们通过模拟一些简单的图能够发现有可能会出现凸出来一块的情况，比如

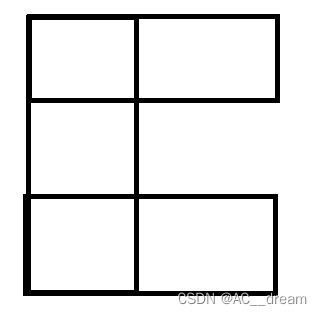
不难发现这种凸出来的方案接下来填充方法是唯一的，就比如左边这个我们必须要在上下各填充一个1*2的小矩形，而右边这种方案只能在中间填充一块1*2的小矩形，但是最后发现这2种方案是不合法的，就是因为这样凸出来一块的方案接下来的填充方案是唯一的，所以才知道最后是否合法，如果合法那么就只有一种连起来的填充方案，否则就没有，通过模拟发现只有下面这两种填充方案是合法的，以填充3*6的为例：

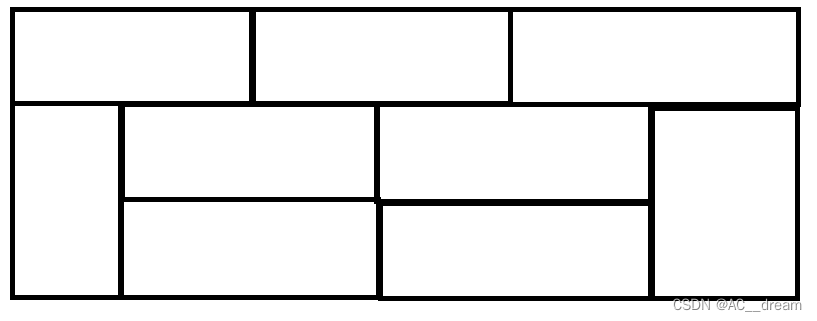
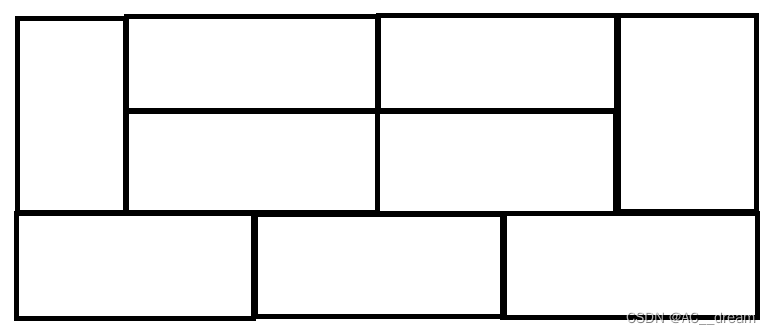
但是至于让多少块连起来这是我们决定的，但是必须是偶数块，也就是说我们可以让任意一个3*n的矩形填充为一个连续的大块，这样的填充方案有2种，比如对于n=6而言，我们可以让后四列填充为一大块，也可以让后六列也就是整体填充为一大块，方案就需要加上2*(f[2]+f[0])，类似的对于n就需要加上2*(f[n-4]+f[n-6]+……+f[0]),分析到这就结束了，这个地方我们可以用前缀和优化一下，细节见代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=31;
long long f[N],s[N];
int main()
{
	int n;
	f[0]=1;f[2]=3;
	s[0]=1;s[2]=4;
	for(int i=3;i<=30;i++)
	{
		f[i]=f[i-2]*3;
		if(i>=4) f[i]+=2*s[i-4];
		if(i%2==0) s[i]=s[i-2]+f[i];
	}
	while(scanf("%d",&n)&&n!=-1)
	{
		printf("%lld\n",f[n]);
	}
	return 0;
}

整数划分

题目链接：2022秋_qdu_算法设计_递归分治[图灵] - Virtual Judge

样例输入：

样例输出：

2
3
10

中文题意不作解释

分析：这是一个经典的动态规划问题，设f[i][j]表示用最大值不超过j且合法的表示i的方案数

递推方程：f[i][j]=f[i][j-1]+f[i-j][min(i-j,j-1)]

f[i][j-1]代表不用j来表示i的方案数，也就是用1~j-1来表示i的方案数，而f[i-j][min(i-j,j-1)]是包含j来表示i的方案数，用上一个j后我们需要表示的数就变为i-j，而且剩余数的最大值不能超过j-1，因为我们已经设定最大值是j，而且已经用过了j，而且最大值也不能超过剩余所需要表示的值i-j，这是显然的，所以表示i-j的最大值就是min(i-j,j-1),细节见代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1003,mod=19901014;
int f[N][N];//f[i][j]表示用最大值不超过j且合法的表示i的方案数 
int main()
{
	int T,n;
	scanf("%d",&T);
	f[0][0]=1;
	for(int i=1;i<=1000;i++)//枚举组成的数
	for(int j=1;j<=i;j++)//枚举最大值 
		f[i][j]=(f[i][j-1]+f[i-j][min(i-j,j-1)])%mod;
	//f[i][j-1]代表不选j,f[i-j][min(i-j,j-1)]代表选j 
	while(T--)
	{
		scanf("%d",&n);
		printf("%d\n",f[n][n]);
	}
	return 0; 
}

HDU3714 Quoit Design

题目链接：Error Curves - HDU 3714 - Virtual Judge

题意：给定n个二次函数a*x*x+b*x+c=0（a>=0），定义f(x)为在x点处n个二次函数的最大值，求在0~1000内f(x)的最小值

分析：由a>=0可知所给的二次函数是下凸函数，那么对于下凸函数极值的求法我们显然可以进行三分，而且通过简单的画图可以发现f(x)的图像是连续的，而且由于所有的二次函数均是下凸函数，f(x)只是由不同的函数的部分区间构成，所以f(x)也是下凸函数，所以我们可以直接三分求解极小值，注意精度的设置不要过小一开始我设置的1e-6，直接wa，后来调高精度就ac了，细节见代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=10003;
long long a[N],b[N],c[N];
int n;
double cal(double x)
{
	double mx=a[1]*x*x+b[1]*x+c[1];
	for(int i=2;i<=n;i++)
		mx=max(mx,a[i]*x*x+b[i]*x+c[i]);
	return mx;
}
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%lld%lld%lld",&a[i],&b[i],&c[i]);
		double l=0.0,r=1000.0;
		while(fabs(r-l)>1e-9)
		{
			double lmid=l+(r-l)/3,rmid=r-(r-l)/3;
			if(cal(lmid)<cal(rmid)) r=rmid;
			else l=lmid;
		}
		printf("%.4lf\n",cal(l));
	}
	return 0;
}

HDU1007 Quoit Design

题目链接：Quoit Design - HDU 1007 - Virtual Judge

样例输入：

样例输出：

0.71
0.00
0.75

题意：给定一个二维平面内的n个点，求一个圆的最小半径，使得这个圆无论怎样移动也不可能使得圆内包含两个点。

分析：思路很显然，就是要我们求得n个点中距离最小的两个点，让其作为圆的直径即可，那么问题就转化为平面最近点对问题，这个是用分治法来解决的，我在之前博客中有介绍，不懂的小伙伴可以看下博客最近点对（分治）_AC__dream的博客-优快云博客，下面直接附代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<queue>
using namespace std;
const int N=100003;
int n;
struct node{
	double x,y;
}p[N];
double dis(node a,node b)
{
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool cmp1(node a,node b)
{
	return a.x<b.x;
}
bool cmp2(node a,node b)
{
	return a.y<b.y;
}
double solve(int l,int r)
{
	if(r-l<3)
	{
		if(r-l==1)
			return dis(p[l],p[r]);
		else
			return min(min(dis(p[l],p[l+1]),dis(p[l],p[r])),dis(p[l+1],p[r]));
	}
	int mid=l+r>>1;
	double d=min(solve(l,mid),solve(mid+1,r));
	vector<node>q;
	for(int i=l;i<=r;i++)
		if((p[i].x-p[mid].x)<d) q.push_back(p[i]);
	sort(q.begin(),q.end(),cmp2);
	for(int i=0;i<q.size();i++)
	{
		for(int j=i+1;j<q.size();j++)
		{
			if(q[j].y-q[i].y>d) break;
			d=min(d,dis(q[i],q[j]));
		}
	}
	return d;
}
int main()
{
	while(true)
	{
		scanf("%d",&n);
		if(n==0) break;
		for(int i=1;i<=n;i++)
			scanf("%lf%lf",&p[i].x,&p[i].y);
		sort(p+1,p+n+1,cmp1);
		printf("%.2lf\n",(solve(1,n)/2));
	}
	return 0;
}