本文深入探讨遗传算法的原理，从起源发展到实际应用。重点讲述了遗传算法在车间布局优化问题中的应用，包括数学模型、评价标准和遗传算法求解过程，并通过实例展示了算法的有效性。
前言
之前只对遗传算法进行了简单的介绍，本文主要针对遗传算法原理，应用案例求解过程进行介绍。
一、遗传算法的形成和发展
示例：遗传算法起源于对生物系统所进行的计算机模拟研究。20世纪60年代初，美国Michigan大学的J. Holland教授受到生物模拟技术的启发开始对其研究，在1966年关于自适应下棋程序的论文中，他应用遗传算法搜索下棋游戏评价函数的参数集，并首次提出了遗传算法这一术语。1965年Holland出版了遗传算法的经典著作《Adaptation Natural and artificial Systems》，系统阐述了遗传算法的基本理论和方法。同年，De Jong完成了他的博士论文《Analysis of the behavior of a class of genetic adaptive systems》，将Holland的模式理论与他的计算试验结合起来，进一步完善了选择、交叉和变异操作，提出了一些新的遗传操作方法。进入80年代后，遗传算法得到了迅速发展，在越来越多的应用领域中得到应用。1983年，Holland的学生Goldberg将遗传算法应用于管道煤气系统的优化，很好地解决了这一非常复杂的问题。在机器学习方面，Holland自提出遗传算法的基本理论后就致力于研究分类器系统（classifier system），Holland 希望系统能将外界刺激进行分类，然后送到需要的地方去，因此命名为分类器系统。之后Holland和其他研究员合作，用分类器系统模拟了一些经济现象，得到了满意的结果。1991年， L. Davis出版了《Handbook of Genetic Algorithm》一书，介绍了遗传算法在科学计算、工程技术和社会经济中的大量应用实例。1992年，John R. Koza将遗传算法应用于计算机程序的优化设计及自动生成，提出了遗传编程(GP: Genetic Programming)的概念。
遗传算法具有鲁棒性强的特点，在解决NP-hard问题方面的能力，引起了国内外学者的广泛重视。近年来，将遗传算法用于求解生产系统优化问题的研究，已经成为研究热点。
二、遗传算法应用实例
1.车间布局优化
1.1 车间设备布局的数学模型
1.1.1 车间设备布局的约束条件
车间设备布局问题作为一种二维的工程实际布局问题，属于带性能约束的二维布局问题，除了总的性能约束外，布局过程还存在着许多其他的布局要求，这些布局要求对布局问题的求解产生了重要的影响。
布局约束可以分为硬约束和软约束。硬约束是指布局中必须满足的约束；如布局物体之间的不干涉约束，即两物体不能重叠。硬约束如果被违反，则布局方案失败。软约束是指在一定程度上应当被满足的约束。通常情况下数学模型中的目标函数就是一种软约束。车间设备布局方案的约束条件主要包括目标约束、模式约束、形状位置约束等等约束条件：
(1)目标约束：车间设备布局的目标是使物流效率最高。这个约束条件是一个软约束条件，也是一种启发式规则。
(2)模式约束：包括布局方案中间各个设备之间的相互关系，如多台相同功能的机床必须成组布置等，这种约束条件属于硬约束条件，在布局设计中要首先加以满足。
(3)形状位置约束：包括布局方案中各个设备与车间之间的相对位置关系的约束条件，主要有：设备之间不能相互干涉，设备之间的相对位置之间要有一定的安全距离，所有布局设备的位置必须位于车间以内，且设备与车间墙壁之间有一定的安全距离，车间内有障碍物和禁止使用的区域(如支柱、水池或者车间办公区域等)。
1.1.2车间设备布局方案的评价标准
物流效率是车间设备布局方案的主要评价指标。物流效率分析包括确定物料在各个加工设备之间的流动顺序，以及单位时间内流动的强度。物料在各个加工设备之间的流动顺序应当是顺序流动，直至所有的工序完成，而没有太多的折返或者倒流的情况。
由于任何一个零部件的加工装配工艺就已经决定了所使用的机床和设备类型，以及其中某一设备的使用次数，所以，对物流效率的分析就转变为对物流强度的分析，以及使布局方案符合生产工艺的需要。对于物流强度的分析和计算可以通过数学建模方式以量化指标表示，如下式。
(F：物流强度，f：设备之间的物流频率矩阵，d：设备之间的距离矩阵，c：设备间物流单位费用矩阵，i， j分别为设备编号)
1.1.3车间设备布局的数学模型
将实际的车间和设备作以下简化，以建立设备布局的数学模型。其中布局容器为车间，待布置物为各种机床设备。将车间和机床简化为一定面积的矩形，车间长宽分别设为L、W，机床设备的长宽分别为S、Q。建立如下图6-2所示的车间平面的直角坐标系，设备的位置直接由设备中心的X、Y坐标值确定(xi, yi)，(xj, yj)。设车间内有n台加工设备参与布局，这n台设备之间的相互的物料传送次数用矩阵f表示；设备间的距离用矩阵d来表示；设备间单位距离的物流费用可用矩阵c来表示：
上述分析中，布局的评价目标是最高的物流效率，即：物流成本最小化，计算公式由上式给出。
约束条件：
(1)布局容器的约束，即布局不能超出车间长L和宽W的限制，需同时满足式；
(2)待布置物之间的不干涉性，即机床的布局位置两两不能相交，即需满足式，满足其一即可。；
(xni , xli分别表示布局中长度方向上两端两台设备横坐标，ynj，ylj分别表示宽度方向上两端两台设备的纵坐标。)
1.2 采用遗传算法求解车间设备布局问题
根据设备布局优化设计的要求，设计两组染色体，即X(设备的横坐标): x1,x2, x3,…xn, Y (设备的纵坐标) : y1 y2 y3 ,…yn。以(x,y)表示设备中心在车间中的坐标位置。
采用一个车间布局实例对比实验，具体的布局参数是：车间长度22m、车间宽度16m；车间包含6台设备，其长宽矩阵S、设备相互之间物流量矩阵f和单位距离物流费用矩阵c分别为：
设备之间的最小安全距离为2米，机器与边界最小间距为2米；要求求解最佳的布局方案。
根据上述分析，定义的适应度值函数为：
公式（6-15）中f(x)表示构造的适应度函数，Max为初始设定的上限值，公式（6-16）对应公式（6-8）和（6-9）约束，公式（6-17）对应公式（6-10）和（6-11）约束。
在遗传算子操作上，对选择算子进行了简化，交叉和变异算子采用标准操作，采用150次迭代时，在111代取得了最优个体X=(6.45,12.82,10.44,4.62,18.46,6.68,1.26 ,5.69,12.54 ,9.64,4.45,1.80)，最优目标值为1.8022e+04。
2.车间布局问题求解代码
function WorkshopLayout()
clear
clc
close all
%PKG：存储每一代的最优解的适应度
%LayoutG：存储每一代最优设备排列方式
DeviceSize=[4,4;3,1.5;6,3.5;2.5,2;2,2;5,3];
Cij=[0,2,4,1.5,1.5,2.5;...
2,0,2.5,1.5,1,2;...
4,2.5,0,2.5,2.5,3;...
1.5,1.5,2.5,0,1,2;...
1.5,1,2.5,1,0,2;...
2.5,2,3,2,2,0];
Fij=[0,31,12,9,28 ,90;...
31,0,21,41,24,62;...
12,21,0,14,12,21;...
9,41,14,0,72,80;...
28,24,12,72,0,40;...
90,62,21,80,40,0];
hi0=[2,2,2,2,2,2];%设备与边界之间距离2m
hij=[0,2,2,2,2,2;...%设备之间安全距离为2m
2,0,2,2,2,2;...
2,2,0,2,2,2;...
2,2,2,0,2,2;...
2,2,2,2,0,2;...
2,2,2,2,2,0];
s=8;
s0=4;
nchr=50; %种群数量
G=150; %代终止数
pc=0.6; %交叉概率
pm=0.1; %变异概率
T=1000; %惩罚系数
H=16; %车间宽度
r=22; %长度
Umin=0;
Umax=1.5;
%% 随机生成nchr个初始种群，用已有设备序列替换掉前三个染色体的设备序列段
%M,由于是对随机矩阵每一行排序后新矩阵的数字在原矩阵的序号，所以M相当于随机生成
%nchr个1到6的随机排序
[sorted,M]=sort(rand(nchr,6),2); %50*6的按列从小到大排序的矩阵
CHR=[M,unifrnd(Umin,Umax,nchr,6)];%50*12的矩阵
for ki=1:3
%用所给的设备序列替换掉前三个染色体的设备序列段??
CHR(ki,1:6)=[1,5,2,4,6,3];
end
%% 以下为计算距离矩阵的函数
%chr为染色体，Dij为返回的距离矩阵
function [Dij,nRow,Layout]=GenerateDistanceMatrix(chr)%chr1*12
m=chr(1:6);%chr的1-6号，编号矩阵，1-6的随机排序矩阵
delta=chr(7:12);%chr的7-12号，0-1.5的随机数
%记录每行的设备号，因为最多为6行，所以采用cell数组
%6台设备，最多放六行
Layout=cell(6,1);
k=1; %染色体设备序列m中第一个设备号
nRow=1; %第一行
while k<6
for kk=k:6%
if sum(DeviceSize(m(k:kk),1))+sum(delta(m(k:kk)))+...
sum(hij(sub2ind(size(hij),m(k:kk-1),m(k+1:kk))))+...%hij6*6,,sub2ind找到矩阵对应位置的索引号
sum(hi0(m([k,kk])))>r%长度,最左边和最右边两台设备到边界距离和
Layout{nRow}=m(k:kk-1);%当几台设备的长度之和大于额定长度时，选取前kk-1台设备作为第一层布局
k=kk;%前kk-1台设备已经被分配，故从kk台设备重新开始
break
end
end
nRow=nRow+1;
%判断是否到最后一台设备
if kk==6
Layout{nRow}=m(kk);%只剩下最后一台设备
else if sum(DeviceSize(m(kk:end),1))+sum(delta(m(kk:end)))+...
sum(hij(sub2ind(size(hij),m(kk:end-1),m(kk+1:end))))+...
sum(hi0(m([kk,end])))<=r
Layout{nRow}=m(kk:end);
break
end
end
end
x=zeros(6,1); %存储各设备x坐标
y=zeros(6,1); %存储各设备y坐标
2. 装箱问题
2.1 模型
与背包问题类似，装箱问题要求从 n 个物品中选取若干装入一个箱子中。每个物品有体积(vi>0)和价值(pi)，每个箱子有体积限制(V0>0)。目标是寻找最优的将物品分配到箱子的方案，使每个箱子中物品的体积之和不超过容积限制，而价值最大。
装箱问题的数学表示如下：
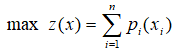
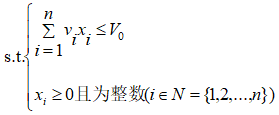
式中，xi＝1表示物品i被装入箱子，xi=0则表示物品i未被选中。
2.2 实例验证
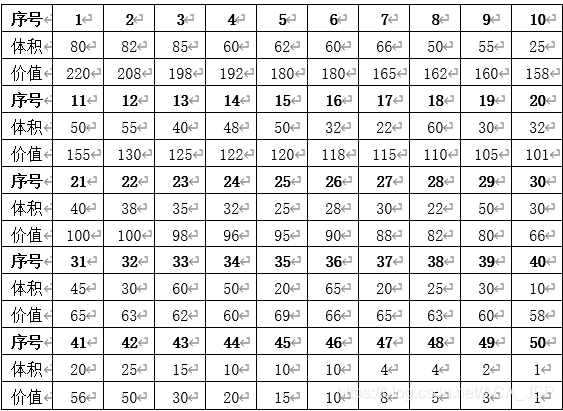
从下面物品中选取若干，在总体积不超过1000情况下使总价值最大。
2.3 代码主函数
clc;clear;
%C=[220,208,198,192,180,180,165,162,160,158,155,130,125,122,120,118,115,110,105,101,100,100, 98,96,95,90,88,82,80,77,75,73,72,70,69,66,65,63,60,58,56, 50,30,20,15,10,8,5,3,1]
%W=[80, 82, 85, 70, 72,70, 66, 50, 55, 25, 50, 55,40, 48, 50,32, 22,60, 30, 32, 40,38, 35,32,25,28,30,22,50,30,45,30,60,50,20,65,20,25,30,10,20, 25,15,10,10,10,4,4,2,1]
bill=[220,80;208,82;198,85;192,70;180,72;180,70;165,66;162,50;160,55;158,25;155,50;130,55;125,40;122,48;120,50;118,32;115,22;110,60;105,30;101,32;100,40;100,38;98,35;96,32;95,25;90,28;88,30;82,22;80,50;77,30;75,45;73,30;72,60;70,50;69,20;66,65;65,20;63,25;60,30;58,10;56,20;50,25;30,15;20,10;15,10;10,10;8,4;5,4;3,2;1,1];
%bill=[10,15;15,25;20,35;25,45;30,55;35,70];
NIND=50;
maxGen=500;
maxWeight = 1000;
[amount,~] = size(bill);
XOVR=0.6; %交叉率
MUTR=0.1; %变异率
trace=zeros(2,maxGen);
%初始化种群
Chrom = zeros(NIND,amount);
for i=1:NIND
weight(i)=0;
for j=1:amount
Chrom(i,j)=randi(2)-1;
weight(i)=weight(i)+Chrom(i,j)*bill(j,2);
end
while weight(i)>maxWeight
weight(i)=0;
for j=1:amount
Chrom(i,j)=randi(2)-1;
weight(i)=weight(i)+Chrom(i,j)*bill(j,2);
end
end
end
%计算初始种群目标函数值
objV=obj(Chrom,bill);
%循环
gen=0;
while gen<maxGen
%计算适应度累计概率
fitV=fit(objV);
%选择
Chrom=select(Chrom,fitV);
%交叉
Chrom = across (Chrom,XOVR);
%检查合法性
[Chrom,objV,weight] = check(Chrom,bill,maxWeight);
%变异
Chrom = aberrance (Chrom,MUTR);
%检查合法性
[Chrom,objV,weight] = check(Chrom,bill,maxWeight);
gen = gen+1;
trace(1,gen) = max(objV);
trace(2,gen) = mean(objV);
end
figure(1)
plot(trace(1,:));
hold on;
plot(trace(2,:),'-.');
grid;
legend('最优值的变化','均值的变化');
optimalValue=max(trace(1,:));
2.4运行结果
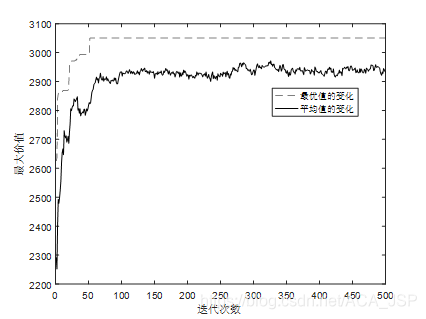
最佳组合结果序号：
1, 2, 4, 5, 8, 9, 10, 11, 13, 14, 16, 16, 19, 20, 21, 22, 24, 25, 26, 26, 28, 35, 36, 40 41, 43, 44, 49
这些箱子体积刚好满足最大容积，总价值为3063.
扫一扫
1184
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
