逻辑回归与线性回归的区别是在输出层加入 sigmoid函数。
使用的数据集是信用卡欺诈数据集credit-a
下载地址:链接:https://pan.baidu.com/s/1eGyb1bzT3x3BLakNmjI7tA 提取码:500l
处理过程
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt
#读取数据集
data = pd.read_csv('dataset/credit-a.csv')
data.head()
| 0 | 30.83 | 0.1 | 0.2 | 0.3 | 9 | 0.4 | 1.25 | 0.5 | 0.6 | 1 | 1.1 | 0.7 | 202 | 0.8 | -1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 58.67 | 4.460 | 0 | 0 | 8 | 1 | 3.04 | 0 | 0 | 6 | 1 | 0 | 43 | 560.0 | -1 |
| 1 | 1 | 24.50 | 0.500 | 0 | 0 | 8 | 1 | 1.50 | 0 | 1 | 0 | 1 | 0 | 280 | 824.0 | -1 |
| 2 | 0 | 27.83 | 1.540 | 0 | 0 | 9 | 0 | 3.75 | 0 | 0 | 5 | 0 | 0 | 100 | 3.0 | -1 |
| 3 | 0 | 20.17 | 5.625 | 0 | 0 | 9 | 0 | 1.71 | 0 | 1 | 0 | 1 | 2 | 120 | 0.0 | -1 |
| 4 | 0 | 32.08 | 4.000 | 0 | 0 | 6 | 0 | 2.50 | 0 | 1 | 0 | 0 | 0 | 360 | 0.0 | -1 |
#从上可以看出此数据集没有表头,把第一行数据当成了表头,重读一遍
data = pd.read_csv('dataset/credit-a.csv',header=None)
data.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 30.83 | 0.000 | 0 | 0 | 9 | 0 | 1.25 | 0 | 0 | 1 | 1 | 0 | 202 | 0.0 | -1 |
| 1 | 1 | 58.67 | 4.460 | 0 | 0 | 8 | 1 | 3.04 | 0 | 0 | 6 | 1 | 0 | 43 | 560.0 | -1 |
| 2 | 1 | 24.50 | 0.500 | 0 | 0 | 8 | 1 | 1.50 | 0 | 1 | 0 | 1 | 0 | 280 | 824.0 | -1 |
| 3 | 0 | 27.83 | 1.540 | 0 | 0 | 9 | 0 | 3.75 | 0 | 0 | 5 | 0 | 0 | 100 | 3.0 | -1 |
| 4 | 0 | 20.17 | 5.625 | 0 | 0 | 9 | 0 | 1.71 | 0 | 1 | 0 | 1 | 2 | 120 | 0.0 | -1 |
#查看第15列结果有几类
data.iloc[:,-1].value_counts()
1 357 -1 296 Name: 15, dtype: int64
是个二分类问题,-1 1 用于SVM,我们要用逻辑回归对其进行处理,所以先把-1 全部替换成0
#构造x,y
x = data.iloc[:,:-1]
y = data.iloc[:,-1].replace(-1,0)
#构建一个 输入为 15 隐藏层为 10 10 输出层为1的神经网络,由于是逻辑回归,最后输出层的激活函数为sigmoid
model = tf.keras.Sequential([
tf.keras.layers.Dense(10,input_shape=(15,),activation='relu'),
tf.keras.layers.Dense(10,activation='relu'),
tf.keras.layers.Dense(1,activation='sigmoid')
])
model.summary()

#设置优化器、损失函数
model.compile(
optimizer = 'adam', #优化器
loss='binary_crossentropy', #损失函数,交叉熵
metrics=['acc'] #准确率
)
#训练80次
history = model.fit(x,y,epochs=80)
In [17]:
#训练80次 history = model.fit(x,y,epochs=80)
x
#训练80次
history = model.fit(x,y,epochs=80)
Train on 653 samples Epoch 1/80 653/653 [==============================] - 0s 59us/sample - loss: 0.4691 - acc: 0.7963 Epoch 2/80 653/653 [==============================] - 0s 43us/sample - loss: 0.3971 - acc: 0.8438 Epoch 3/80 653/653 [==============================] - 0s 43us/sample - loss: 0.3794 - acc: 0.8484 Epoch 4/80 653/653 [==============================] - 0s 55us/sample - loss: 0.3665 - acc: 0.8545 Epoch 5/80 653/653 [==============================] - 0s 62us/sample - loss: 0.4101 - acc: 0.8300 Epoch 6/80 653/653 [==============================] - 0s 45us/sample - loss: 0.3759 - acc: 0.8423 Epoch 7/80 653/653 [==============================] - 0s 37us/sample - loss: 0.3732 - acc: 0.8423 Epoch 8/80 653/653 [==============================] - 0s 39us/sample - loss: 0.3724 - acc: 0.8530 Epoch 9/80 653/653 [==============================] - 0s 57us/sample - loss: 0.3982 - acc: 0.8453 Epoch 10/80 653/653 [==============================] - 0s 58us/sample - loss: 0.3757 - acc: 0.8438 Epoch 11/80 653/653 [==============================] - 0s 47us/sample - loss: 0.3658 - acc: 0.8576 Epoch 12/80 653/653 [==============================] - 0s 34us/sample - loss: 0.3795 - acc: 0.8499 Epoch 13/80 653/653 [==============================] - 0s 36us/sample - loss: 0.3788 - acc: 0.8484 Epoch 14/80 653/653 [==============================] - 0s 36us/sample - loss: 0.6189 - acc: 0.8116 Epoch 15/80 653/653 [==============================] - 0s 38us/sample - loss: 0.3756 - acc: 0.8392 Epoch 16/80 653/653 [==============================] - 0s 40us/sample - loss: 0.3777 - acc: 0.8576 Epoch 17/80 653/653 [==============================] - 0s 49us/sample - loss: 0.3665 - acc: 0.8530 Epoch 18/80 653/653 [==============================] - 0s 28us/sample - loss: 0.3702 - acc: 0.8484 Epoch 19/80 653/653 [==============================] - 0s 38us/sample - loss: 0.3616 - acc: 0.8484 Epoch 20/80 653/653 [==============================] - 0s 35us/sample - loss: 0.3621 - acc: 0.8560 Epoch 21/80 653/653 [==============================] - 0s 47us/sample - loss: 0.3624 - acc: 0.8545 Epoch 22/80 653/653 [==============================] - 0s 40us/sample - loss: 0.3686 - acc: 0.8484 Epoch 23/80 653/653 [==============================] - 0s 41us/sample - loss: 0.3514 - acc: 0.8698 Epoch 24/80 653/653 [==============================] - 0s 39us/sample - loss: 0.3626 - acc: 0.8622 Epoch 25/80 653/653 [==============================] - 0s 53us/sample - loss: 0.3973 - acc: 0.8530 Epoch 26/80 653/653 [==============================] - 0s 31us/sample - loss: 0.3505 - acc: 0.8652 Epoch 27/80 653/653 [==============================] - 0s 42us/sample - loss: 0.3480 - acc: 0.8668 Epoch 28/80 653/653 [==============================] - 0s 31us/sample - loss: 0.3453 - acc: 0.8683 Epoch 29/80 653/653 [==============================] - 0s 46us/sample - loss: 0.3333 - acc: 0.8698 Epoch 30/80 653/653 [==============================] - 0s 50us/sample - loss: 0.3608 - acc: 0.8576 Epoch 31/80 653/653 [==============================] - 0s 49us/sample - loss: 0.3616 - acc: 0.8637 Epoch 32/80 653/653 [==============================] - 0s 35us/sample - loss: 0.3609 - acc: 0.8515 Epoch 33/80 653/653 [==============================] - 0s 37us/sample - loss: 0.4148 - acc: 0.8484 Epoch 34/80 653/653 [==============================] - 0s 44us/sample - loss: 1.3700 - acc: 0.7825 Epoch 35/80 653/653 [==============================] - 0s 48us/sample - loss: 0.6737 - acc: 0.7933 Epoch 36/80 653/653 [==============================] - 0s 43us/sample - loss: 0.4980 - acc: 0.8025 Epoch 37/80 653/653 [==============================] - 0s 48us/sample - loss: 0.4042 - acc: 0.8423 Epoch 38/80 653/653 [==============================] - 0s 43us/sample - loss: 0.3452 - acc: 0.8698 Epoch 39/80 653/653 [==============================] - 0s 36us/sample - loss: 0.3442 - acc: 0.8683 Epoch 40/80 653/653 [==============================] - 0s 44us/sample - loss: 0.3456 - acc: 0.8683 Epoch 41/80 653/653 [==============================] - 0s 43us/sample - loss: 0.3456 - acc: 0.8683 Epoch 42/80 653/653 [==============================] - 0s 44us/sample - loss: 0.3377 - acc: 0.8714 Epoch 43/80 653/653 [==============================] - 0s 44us/sample - loss: 0.3409 - acc: 0.8591 Epoch 44/80 653/653 [==============================] - 0s 44us/sample - loss: 0.3465 - acc: 0.8606 Epoch 45/80 653/653 [==============================] - 0s 52us/sample - loss: 0.3270 - acc: 0.8760 Epoch 46/80 653/653 [==============================] - 0s 45us/sample - loss: 0.3337 - acc: 0.8760 Epoch 47/80 653/653 [==============================] - 0s 41us/sample - loss: 0.3326 - acc: 0.8683 Epoch 48/80 653/653 [==============================] - 0s 41us/sample - loss: 0.3269 - acc: 0.8698 Epoch 49/80 653/653 [==============================] - 0s 49us/sample - loss: 0.3284 - acc: 0.8729 Epoch 50/80 653/653 [==============================] - 0s 28us/sample - loss: 0.3311 - acc: 0.8790 Epoch 51/80 653/653 [==============================] - 0s 43us/sample - loss: 0.3242 - acc: 0.8821 Epoch 52/80 653/653 [==============================] - 0s 39us/sample - loss: 0.3220 - acc: 0.8714 Epoch 53/80 653/653 [==============================] - 0s 40us/sample - loss: 0.3742 - acc: 0.8606 Epoch 54/80 653/653 [==============================] - 0s 55us/sample - loss: 0.3976 - acc: 0.8438 Epoch 55/80 653/653 [==============================] - 0s 31us/sample - loss: 0.3378 - acc: 0.8806 Epoch 56/80 653/653 [==============================] - 0s 38us/sample - loss: 0.4113 - acc: 0.8530 Epoch 57/80 653/653 [==============================] - 0s 42us/sample - loss: 0.5724 - acc: 0.8254 Epoch 58/80 653/653 [==============================] - 0s 25us/sample - loss: 0.4780 - acc: 0.8377 Epoch 59/80 653/653 [==============================] - 0s 33us/sample - loss: 0.4665 - acc: 0.8300 Epoch 60/80 653/653 [==============================] - 0s 44us/sample - loss: 0.3649 - acc: 0.8668 Epoch 61/80 653/653 [==============================] - 0s 44us/sample - loss: 0.3242 - acc: 0.8744 Epoch 62/80 653/653 [==============================] - 0s 45us/sample - loss: 0.3166 - acc: 0.8821 Epoch 63/80 653/653 [==============================] - 0s 44us/sample - loss: 0.3236 - acc: 0.8729 Epoch 64/80 653/653 [==============================] - 0s 29us/sample - loss: 0.3264 - acc: 0.8760 Epoch 65/80 653/653 [==============================] - 0s 45us/sample - loss: 0.3227 - acc: 0.8806 Epoch 66/80 653/653 [==============================] - 0s 40us/sample - loss: 0.3116 - acc: 0.8821 Epoch 67/80 653/653 [==============================] - 0s 50us/sample - loss: 0.3161 - acc: 0.8836 Epoch 68/80 653/653 [==============================] - 0s 41us/sample - loss: 0.3159 - acc: 0.8775 Epoch 69/80 653/653 [==============================] - 0s 38us/sample - loss: 0.3270 - acc: 0.8683 Epoch 70/80 653/653 [==============================] - 0s 32us/sample - loss: 0.3424 - acc: 0.8668 Epoch 71/80 653/653 [==============================] - 0s 51us/sample - loss: 0.3242 - acc: 0.8698 Epoch 72/80 653/653 [==============================] - 0s 45us/sample - loss: 0.3218 - acc: 0.8698 Epoch 73/80 653/653 [==============================] - 0s 45us/sample - loss: 0.3145 - acc: 0.8790 Epoch 74/80 653/653 [==============================] - 0s 31us/sample - loss: 0.3110 - acc: 0.8698 Epoch 75/80 653/653 [==============================] - 0s 51us/sample - loss: 0.3248 - acc: 0.8729 Epoch 76/80 653/653 [==============================] - 0s 43us/sample - loss: 0.3226 - acc: 0.8851 Epoch 77/80 653/653 [==============================] - 0s 33us/sample - loss: 0.3285 - acc: 0.8698 Epoch 78/80 653/653 [==============================] - 0s 35us/sample - loss: 0.3183 - acc: 0.8683 Epoch 79/80 653/653 [==============================] - 0s 25us/sample - loss: 0.3041 - acc: 0.8775 Epoch 80/80 653/653 [==============================] - 0s 36us/sample - loss: 0.3186 - acc: 0.8760
#查看history中都有些啥
history.history.keys()
dict_keys(['loss', 'acc'])
#绘制训练次数与loss的图像
plt.plot(history.epoch, history.history.get('loss'))
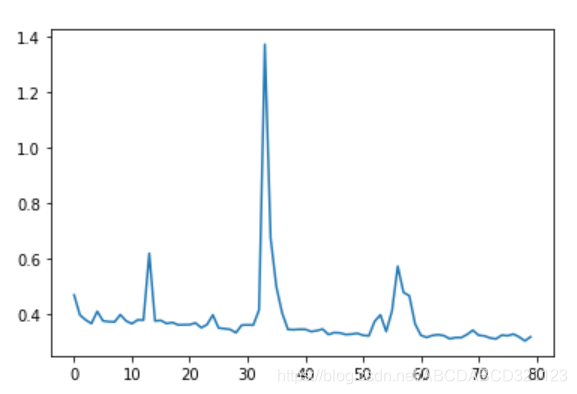
#绘制训练次数与准确率的图像
plt.plot(history.epoch, history.history.get('acc'))
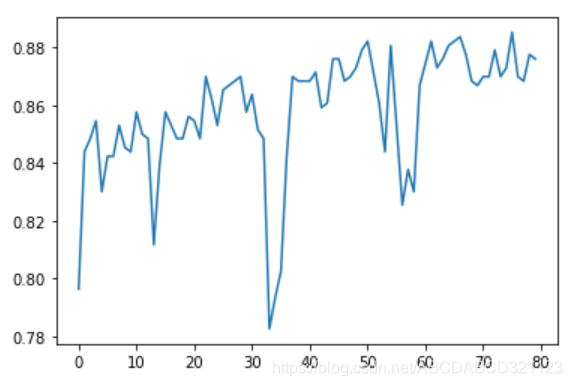





 本文使用逻辑回归算法处理信用卡欺诈数据集,通过构建神经网络并应用sigmoid激活函数,实现对欺诈行为的有效识别。
本文使用逻辑回归算法处理信用卡欺诈数据集,通过构建神经网络并应用sigmoid激活函数,实现对欺诈行为的有效识别。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








