基于PSO-LSTM的时间序列预测：新手友好MATLAB实战-优快云博客

PSO-LSTM时间序列，基于粒子群算法优化长短期记忆神经网络(PSO-LSTM)的时间序列预测需要分类和回归也可更换 MATLAB代码，中文注释清晰，非常适合新手小白替换数据即可运行，推荐2018B以上版本，

在时间序列预测领域，基于粒子群算法优化长短期记忆神经网络（PSO-LSTM）是一种强大的方法。它结合了粒子群算法（PSO）的全局寻优能力和长短期记忆神经网络（LSTM）处理时间序列数据的优势，无论是分类还是回归任务，都能展现出色的性能。今天，咱们就来聊聊这个适合新手小白的MATLAB实现。

1. 整体思路

粒子群算法就像是一群鸟儿在寻找食物，每只鸟（粒子）代表一个可能的解，它们通过自身的经验和群体中最优粒子的经验来调整飞行方向，最终找到全局最优解。而LSTM网络擅长处理具有长期依赖关系的数据，比如时间序列。我们用PSO来优化LSTM网络的参数，使得LSTM在时间序列预测任务中能达到更好的效果。

2. MATLAB代码及分析

% 加载数据，这里假设数据保存在data.mat文件中
load('data.mat'); 
% 数据格式假设为一个列向量，代表时间序列数据
timeSeriesData = data; 

% 划分训练集和测试集，这里简单地按照70%训练，30%测试划分
trainRatio = 0.7; 
trainSize = floor(length(timeSeriesData) * trainRatio); 
trainData = timeSeriesData(1:trainSize); 
testData = timeSeriesData(trainSize + 1:end); 

% 构建LSTM网络结构
numFeatures = 1; % 输入特征维度，这里时间序列数据本身就是一个特征
numResponses = 1; % 输出维度，预测一个值
numHiddenUnits = 100; % 隐藏层神经元数量，可调整

layers = [...
    sequenceInputLayer(numFeatures)
    lstmLayer(numHiddenUnits)
    fullyConnectedLayer(numResponses)
    regressionLayer]; % 如果是分类任务，这里改为softmaxLayer和classificationLayer

% 设置训练选项
options = trainingOptions('adam',...
    'MaxEpochs',100,...
    'GradientThreshold',1,...
    'InitialLearnRate',0.001,...
    'LearnRateSchedule','piecewise',...
    'LearnRateDropFactor',0.2,...
    'LearnRateDropPeriod',10,...
    'Shuffle','every-epoch',...
    'Plots','training-progress');

% 粒子群算法优化部分参数（这里简单以隐藏层神经元数量为例）
numParticles = 20; % 粒子数量
numIterations = 50; % 迭代次数

% 初始化粒子位置和速度，这里隐藏层神经元数量范围设为[50, 200]
particlePositions = randi([50, 200], numParticles, 1); 
particleVelocities = zeros(numParticles, 1); 

% 记录每个粒子的最优位置和全局最优位置
pBestPositions = particlePositions; 
pBestFitness = Inf(numParticles, 1); 
gBestPosition = []; 
gBestFitness = Inf; 

for iter = 1:numIterations
    for i = 1:numParticles
        % 根据当前粒子位置调整隐藏层神经元数量
        numHiddenUnits = particlePositions(i); 
        layers(2) = lstmLayer(numHiddenUnits); 
        % 训练网络
        net = trainNetwork(trainData, trainData, layers, options); 
        % 预测测试集
        predictions = predict(net, testData); 
        % 计算适应度，这里以均方误差为例
        fitness = mean((predictions - testData).^2); 
        % 更新粒子的最优位置
        if fitness < pBestFitness(i)
            pBestFitness(i) = fitness; 
            pBestPositions(i) = particlePositions(i); 
        end
        % 更新全局最优位置
        if fitness < gBestFitness
            gBestFitness = fitness; 
            gBestPosition = particlePositions(i); 
        end
    end
    % 更新粒子速度和位置
    w = 0.7; % 惯性权重
    c1 = 1.5; % 自我认知系数
    c2 = 1.5; % 社会认知系数
    for i = 1:numParticles
        r1 = rand; 
        r2 = rand; 
        particleVelocities(i) = w * particleVelocities(i) +...
            c1 * r1 * (pBestPositions(i) - particlePositions(i)) +...
            c2 * r2 * (gBestPosition - particlePositions(i)); 
        particlePositions(i) = particlePositions(i) + particleVelocities(i); 
        % 确保隐藏层神经元数量在合理范围内
        particlePositions(i) = max(50, min(200, particlePositions(i))); 
    end
end

% 使用全局最优参数重新构建并训练网络
numHiddenUnits = gBestPosition; 
layers(2) = lstmLayer(numHiddenUnits); 
net = trainNetwork(trainData, trainData, layers, options); 
% 最终预测
finalPredictions = predict(net, testData); 

% 绘制结果
figure;
plot(testData, 'b', 'DisplayName', '真实值');
hold on;
plot(finalPredictions, 'r--', 'DisplayName', '预测值');
legend;
xlabel('时间步');
ylabel('数值');
title('PSO-LSTM时间序列预测结果');

代码分析

数据加载与划分：从data.mat文件加载数据，并简单地按照比例划分训练集和测试集。这一步确保我们有数据用于训练和评估模型。
LSTM网络构建：定义了一个基本的LSTM网络结构，包括输入层、LSTM层、全连接层和回归层（如果是分类任务需替换为相应层）。隐藏层神经元数量numHiddenUnits作为可调整参数，后面会用PSO来优化。
训练选项设置：使用trainingOptions设置训练的参数，如优化器为adam，最大训练轮数、学习率等参数。这些参数对模型训练效果有重要影响。
PSO优化部分：初始化粒子群的位置、速度等信息，在每次迭代中，根据粒子位置调整LSTM网络的隐藏层神经元数量，训练网络并计算适应度（这里用均方误差衡量），更新粒子的最优位置和全局最优位置，最后根据公式更新粒子速度和位置，确保参数在合理范围内。
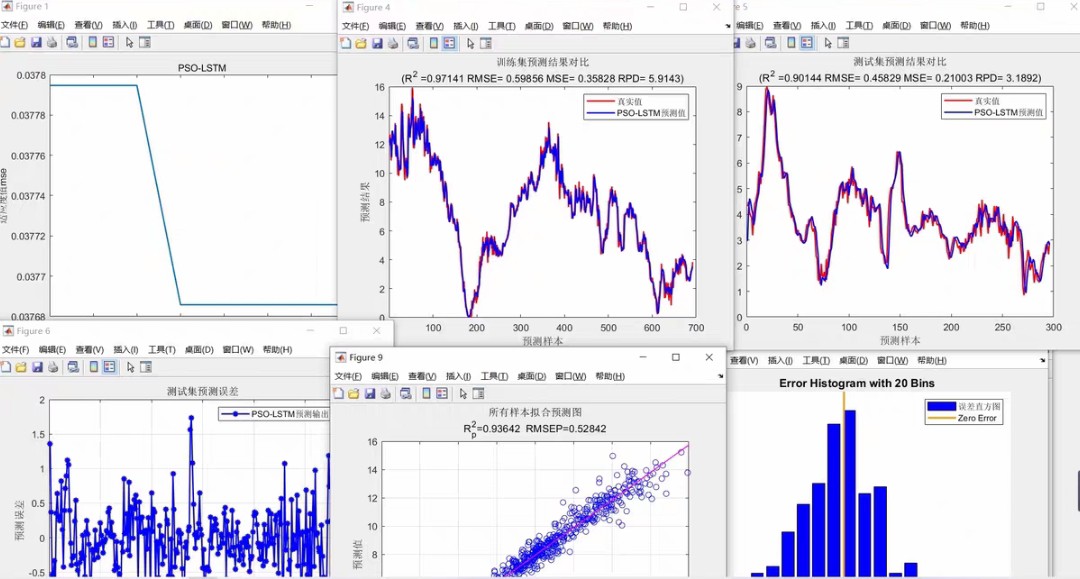
最终训练与预测：使用全局最优参数重新构建并训练网络，得到最终的预测结果，并绘制真实值和预测值的对比图，直观展示预测效果。