目录:
前言:
在上一篇博客中,我们基于 char类型实现了一个简单的链式栈结构(点击跳转)。虽然功能完整,但这种特定类型的实现存在明显的局限性——无法灵活适配其他数据类型,代码的复用性较低。
为了突破这一限制,本文我们将对原有栈结构进行重要升级:引入泛型(Generics),将其改造为一个通用、类型安全的链栈。通过这一改造,我们的栈将能轻松承载任意类型的数据,从而大幅提升代码的复用性和工程实用价值。跳转泛型
此外,我们将继续深入数据结构与算法的核心话题,完整讲解上篇未完成的经典问题:汉诺塔(Hanoi Tower)的递归解法,并进一步探讨递归思想的本质与其性能瓶颈——最后,我们将通过 “递归消除”技术,演示如何手动使用栈来模拟递归过程,从而加深对函数调用机制的理解,并掌握优化递归算法的有效手段。
代码分享:
import java.util.Scanner;
//我发现不能只用单一的char,int做例子,应该用到<T>泛型,这样什么都能用
// LinkStack 类需要声明泛型参数 T
public class LinkStack<T> {
LStackNode<T> top; // 使用泛型类型
LinkStack() {
top = new LStackNode<T>(null); // 修正:使用泛型类型
}
public boolean StackEmpty() {
return top.next == null;
}
public void PushStack(T e) { // 使用泛型类型 T
LStackNode<T> temp = new LStackNode<T>(e); // 修正:使用泛型类型
temp.next = top.next;
top.next = temp;
}
public T PopStack() throws Exception { // 返回类型改为 T
if (StackEmpty()) {
throw new Exception("Stack is Empty");
} else {
LStackNode<T> temp = top.next; // 修正:使用泛型类型
top.next = temp.next;
return temp.data;
}
}
public T GetTop() throws Exception { // 返回类型改为 T
if (StackEmpty()) {
throw new Exception("Stack is Empty");
} else {
return top.next.data;
}
}
public int StackLength() {
LStackNode<T> temp = top.next; // 修正:使用泛型类型
int len = 0;
while (temp != null) {
temp = temp.next;
len++;
}
return len;
}
public void CreatStack() {
System.out.println("输入需要输入栈的字符,用空格分开");
Scanner myScanner = new Scanner(System.in);
String str = myScanner.nextLine();
String[] strs = str.split(" ");
for (int i = 0; i < strs.length; i++) {
if (!strs[i].isEmpty()) {
// 由于是泛型栈,需要将字符转换为泛型类型
// 这里假设 T 是 Character
char c = strs[i].charAt(0);
T element = (T) Character.valueOf(c); // 转换为泛型类型
PushStack(element);
}
}
}
public void show() {
if (StackEmpty()) {
System.out.println("栈为空");
return;
}
LStackNode<T> current = top.next; // 修正:使用泛型类型
System.out.println("栈结构(栈顶在上方):");
System.out.println("┌───┐");
while (current != null) {
System.out.println("│ " + current.data + " │");
System.out.println("└───┘");
current = current.next;
}
System.out.println(" 栈底 ");
}
public static void covert10to8(int x, int[] num){
LStackNode<Integer> top = new LStackNode<Integer>(null), p; // 添加泛型类型
while(x != 0){
p = new LStackNode<Integer>(x % 8);
p.next = top;
top = p;
x = x / 8;
}
int k = 0;
while(top != null && top.data != null){
p = top;
num[k++] = p.data;
top = top.next;
}
for (int i = 0; i < k; i++) {
System.out.print(num[i] );
}
}
}
// LStackNode 类也需要声明泛型参数
class LStackNode<T> {
T data;
LStackNode<T> next; // 修正:使用泛型类型
public LStackNode(T data) {
this.data = data;
this.next = null;
}
}public class HanoiTower{
public static void main(String[] args){
T text = new T();
text.move(3,'A','B','C');
}
}
class T{
public void move(int num,char a,char b , char c){
//思考,当我们有两个盘的时候,那么就先把上面的放到b,再将下面的放到c,
// 再把原本b位置的圆盘移到c
//a:起始点 b:途径(借用) c:终点
if (num == 1){
//如果只有一个,就直接放
System.out.println(a + "->" + c);
}else{//当是两个盘或者大于两个盘的时候,看做两个盘,将最下面的放到c,另一个放到b
//1,把其他的(也就是上面的)放到b,
move(num-1 , a , c , b);
//2.把最下面的一个盘放到c,也就是a + "->" + c
System.out.println(a + "->" + c);
//3.把上面的放到c
move(num-1 , b , a , c);
}
}
}
public class Eliminate {
public static int fact(int n) {
if (n == 1) {
return 1;
}
return n * fact(n - 1);
}
public static long fact2(int n) {
final int MAXSIZE = 50;
long s[][] = new long[MAXSIZE][2];
int top = -1;
++top;
s[top][0] = n;
s[top][1] = 0;
do{
if(s[top][0] == 1){
s[top][1] = 1;
System.out.println("n="+s[top][0]+" fact="+s[top][1]);
}
if(s[top][0] > 1 && s[top][1] == 0){
top = top + 1;
s[top][0] = s[top-1][0]-1;
s[top][1] = 0;
System.out.println("n="+s[top][0]+" fact="+s[top][1]);
}
if(s[top][1] != 0){
s[top-1][1] = s[top][1]*s[top-1][0];
System.out.println("n="+s[top - 1][0]+" fact="+s[top - 1][1]);
top = top - 1;
}
}while(top > 0);
return s[top][1];
}
public static void main(String[] args) {
System.out.println(fact(4));fact(4);
fact2(4);
}
}
一、从Char到泛型:完整转换过程
1.1 原始Char版本代码分析
public class LinkStack {
LStackNode top;
class LStackNode {
char data; // 固定为char类型
LStackNode next;
}
public void PushStack(char e) {
// 只能处理char类型数据
}
}1.2 泛型转换的核心步骤
转换后的泛型版本:
public class LinkStack<T> {
private LStackNode<T> top;
// 泛型节点定义
private static class LStackNode<T> {
T data; // 泛型数据类型
LStackNode<T> next;
public LStackNode(T data) {
this.data = data;
this.next = null;
}
}
public void PushStack(T element) {
LStackNode<T> newNode = new LStackNode<>(element);
newNode.next = top;
top = newNode;
}
public T PopStack() {
if (top == null) throw new IllegalStateException("Stack is empty");
T data = top.data;
top = top.next;
return data;
}
}1.3 转换的深层原因解析
类型安全性的提升:
// 原始版本 - 类型不安全
char data = (char) stack.PopStack(); // 需要强制转换
// 泛型版本 - 编译时类型检查
Integer data = integerStack.PopStack(); // 无需转换,类型安全代码复用性的质的飞跃:
// 可以创建多种类型的栈实例
LinkStack<Integer> intStack = new LinkStack<>();
LinkStack<String> stringStack = new LinkStack<>();
LinkStack<Double> doubleStack = new LinkStack<>();二、Convert10to8方法深度解析
2.1 方法实现与算法原理
public static void covert10to8(int x, int[] num){
LStackNode<Integer> top = new LStackNode<Integer>(null), p; // 添加泛型类型
while(x != 0){
p = new LStackNode<Integer>(x % 8);
p.next = top;
top = p;
x = x / 8;
}
int k = 0;
while(top != null && top.data != null){
p = top;
num[k++] = p.data;
top = top.next;
}
for (int i = 0; i < k; i++) {
System.out.print(num[i] );
}
}2.2 算法可视化演示
以十进制数1568为例:
计算过程:
1568 ÷ 8 = 196 ... 0 → 压栈: 0
196 ÷ 8 = 24 ... 4 → 压栈: 4
24 ÷ 8 = 3 ... 0 → 压栈: 0
3 ÷ 8 = 0 ... 3 → 压栈: 3
栈中内容: [0, 4, 0, 3] (栈顶为3)
出栈顺序: 3, 0, 4, 0 → 八进制结果: 30402.3 Main方法
public class Main {
public static void main(String[] args) {
int[] a = new int[10];
LinkStack.covert10to8(1568,a);
}
}
2.4 运行结果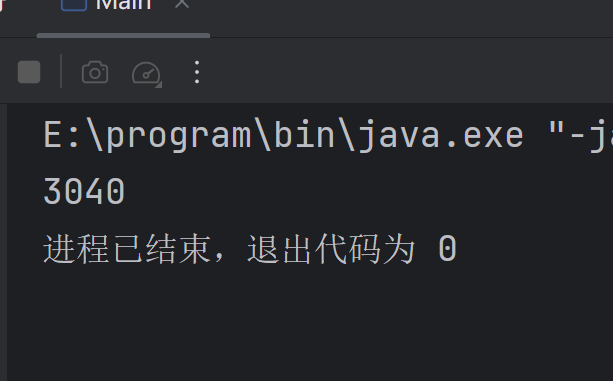
三、递归算法深度剖析
3.1汉诺塔
3.1.1汉诺塔讲解
汉诺塔问题起源于1883年,由法国数学家爱德华·卢卡斯提出,他将其描述为一个带有神秘色彩的传说:印度某座神庙的僧侣们奉命移动64个大小不同的金盘,当任务完成时,世界将会毁灭。这个看似简单的游戏,其核心机制揭示了递归思想的精髓:通过递归分解将复杂问题简化为相同结构的子问题。具体来说,移动n个圆盘的过程被分解为三个关键步骤:首先将上面的n-1个圆盘借助目标柱移到辅助柱,然后将最底层的最大圆盘直接移到目标柱,最后再将辅助柱上的n-1个圆盘借助起始柱移到目标柱。这种分解使得每一步都转化为规模更小的相同问题(移动n-1个圆盘),直到仅剩一个圆盘时可直接移动,成为递归的基准情形。递归的巧妙之处在于通过函数调用栈自动保存中间状态——每次递归调用都会暂停当前任务并优先处理子问题,待子问题解决后自动回溯并完成剩余操作。这种“分而治之”的策略不仅确保了移动过程中始终遵守“大盘不能压小盘”的规则,更深刻地揭示了递归与栈数据结构在问题求解中的内在统一性,使其成为计算机科学中理解算法思想的经典范例。
3.1.2 汉诺塔递归实现
public class HanoiTower{
public static void main(String[] args){
T text = new T();
text.move(3,'A','B','C');
}
}
class T{
public void move(int num,char a,char b , char c){
//思考,当我们有两个盘的时候,那么就先把上面的放到b,再将下面的放到c,
// 再把原本b位置的圆盘移到c
//a:起始点 b:途径(借用) c:终点
if (num == 1){
//如果只有一个,就直接放
System.out.println(a + "->" + c);
}else{//当是两个盘或者大于两个盘的时候,看做两个盘,将最下面的放到c,另一个放到b
//1,把其他的(也就是上面的)放到b,
move(num-1 , a , c , b);
//2.把最下面的一个盘放到c,也就是a + "->" + c
System.out.println(a + "->" + c);
//3.把上面的放到c
move(num-1 , b , a , c);
}
}
}递归调用树分析(n=3):
solveHanoi(3, A, C, B)
├── solveHanoi(2, A, B, C)
│ ├── solveHanoi(1, A, C, B) → 移动1: A→C
│ ├── 移动盘子2: A→B
│ └── solveHanoi(1, C, B, A) → 移动1: C→B
├── 移动盘子3: A→C
└── solveHanoi(2, B, C, A)
├── solveHanoi(1, B, A, C) → 移动1: B→A
├── 移动盘子2: B→C
└── solveHanoi(1, A, C, B) → 移动1: A→C3.1.3 运行结果
3.2 阶乘的递归与迭代实现对比
3.2.1递归版本:
public class Eliminate {
public static int fact(int n) {
if (n == 1) {
return 1;
}
return n * fact(n - 1);
}
3.2.2迭代版本(消除递归):
public static int factorialIterative(int n) {
int result = 1;
for (int i = 2; i <= n; i++) {
result *= i; // 使用循环代替递归
}
return result;
}3.2.3递归消除的高级技巧——使用栈模拟递归调用:
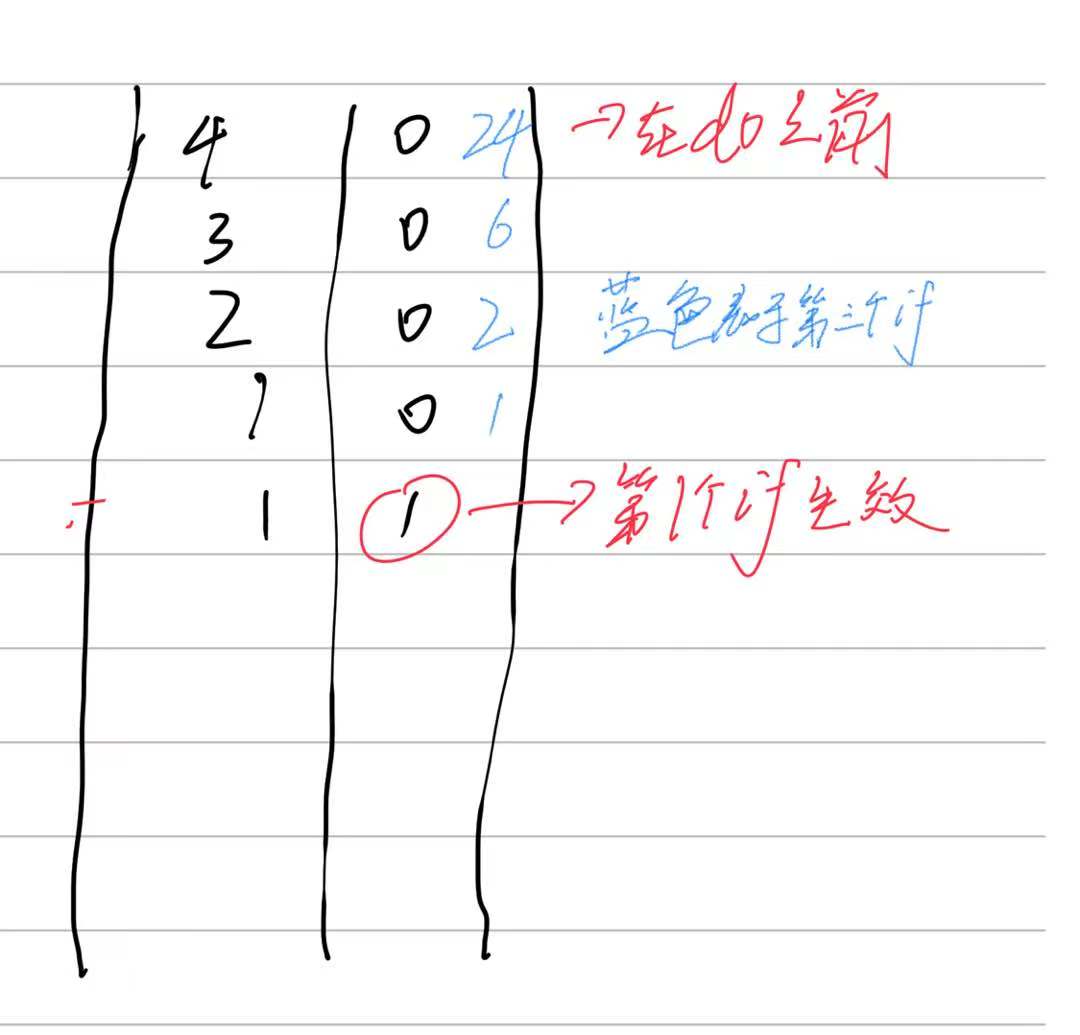
public static long fact2(int n) {
// 定义栈的最大容量
final int MAXSIZE = 50;
// 创建栈数组:s[i][0]存储参数n,s[i][1]存储计算结果fact(n)
long s[][] = new long[MAXSIZE][2];
// 栈顶指针,初始为-1表示空栈
int top = -1;
// 将初始问题n入栈
++top;
s[top][0] = n; // 存储参数n
s[top][1] = 0; // 0表示尚未计算结果
// 使用循环模拟递归过程
do {
// 情况1:到达递归基准情形(n=1)
if(s[top][0] == 1) {
s[top][1] = 1; // fact(1) = 1
System.out.println("n="+s[top][0]+" fact="+s[top][1]);
}
// 情况2:需要继续递归(n>1且尚未计算)
if(s[top][0] > 1 && s[top][1] == 0) {
// 创建新的递归调用:计算fact(n-1)
top = top + 1;
s[top][0] = s[top-1][0]-1; // 参数变为n-1
s[top][1] = 0; // 标记为未计算
System.out.println("n="+s[top][0]+" fact="+s[top][1]);
}
// 情况3:子问题已解决,可以回退计算
if(s[top][1] != 0) {
// 使用子问题的结果计算当前问题:fact(n) = n * fact(n-1)
s[top-1][1] = s[top][1] * s[top-1][0];
System.out.println("n="+s[top - 1][0]+" fact="+s[top - 1][1]);
// 弹出已解决的子问题,栈顶指针减1
top = top - 1;
}
} while(top > 0); // 当栈中只剩最后一个元素时结束
return s[top][1]; // 返回最终结果
}运行结果:(这里传入的n为4)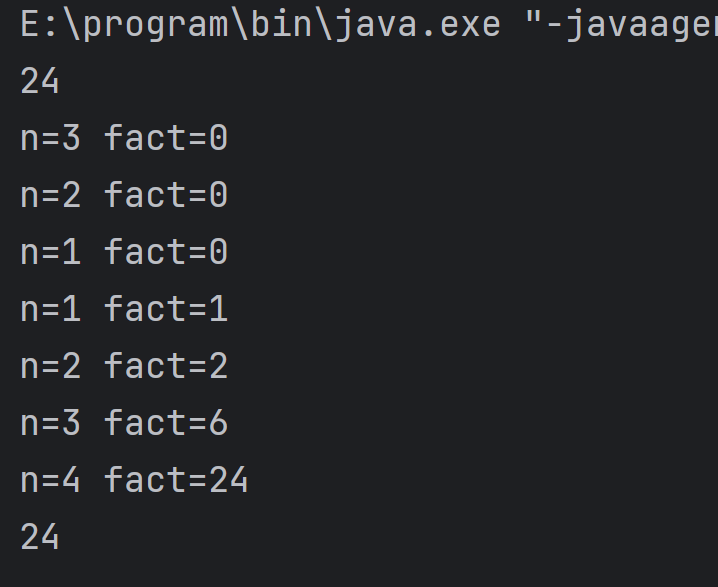
大致图像:
技术总结
本次技术探讨完成了一次从特化到通用、从应用到原理的深入实践,核心内容可归纳为以下三个层面:
1. 泛型化改造:提升代码的抽象与复用能力
核心价值:将基于 char类型的链栈成功升级为泛型栈 LinkStack<T>,解决了原始代码类型固定、复用性差的根本缺陷。
关键步骤:通过引入类型参数 <T>,将节点数据域、栈操作方法中的具体类型 char替换为泛型 T,使栈能够安全地存储和管理任意类型的对象。
重要收获:理解了泛型在编译时提供类型安全、避免运行时强制类型转换的优势,并掌握了实现一个通用数据结构的基本方法。
2. 栈结构的经典应用:深入理解“后进先出”的本质
十进制转八进制(convert10to8):利用栈的LIFO特性,自然地将计算余数的顺序(从低位到高位)逆序为输出结果的正序(从高位到低位),完美解决了数制转换中的逆序问题。
汉诺塔问题(递归解法):递归解法本身隐含了一个函数调用栈。每一步递归调用都将当前任务状态(盘子数、柱子角色)压栈,在基准情形触发后逐层回溯出栈,优雅地解决了复杂移动步骤的跟踪问题。这深刻揭示了递归的本质就是栈操作。
3. 递归消除:透过现象看本质的优化手段
阶乘的递归与迭代对比:直观展示了递归在代码简洁性上的优势,以及迭代在内存效率上的优势。
手动栈模拟递归(fact2方法):这是本次最核心的升华点。通过使用数组显式模拟系统栈(存储参数和返回值),我们亲手实现了递归过程的运转机制。这不仅证明了任何递归算法都可通过栈转换为迭代算法,更极大地深化了对程序运行时函数调用机制的理解,为后续优化递归算法(如防止栈溢出)提供了关键技术路径。
总结而言, 本次内容形成了一个完整的认知闭环:从重构数据结构(泛型栈)到应用数据结构(数制转换),再到理解与模拟数据结构(递归与栈),层层递进。这不仅是一次编程练习,更是一次对计算机科学核心思想——抽象、分层与转化的生动诠释。
大家可以试试看对汉诺塔进行非递归改写,至于为什么我在这里没展现出来,是因为我写不出来了嘻嘻,没时间了。
致谢与邀请
技术之路,始于分享,成于交流。感谢每一位读到这里的同行者。
如果您有更好的实现思路、发现文中的任何问题,或者希望接下来探讨哪些主题,都非常欢迎在评论区留言。让我们保持对话,一起构建这个互相帮助、共同成长的技术学习圈。
下期预告:
队























——从Char到泛型:链栈的抽象、递归的瓦解与栈模拟实现&spm=1001.2101.3001.5002&articleId=155207170&d=1&t=3&u=c568acdf448d47d19e85d593e405eab8)
 1223
1223










