使用分治法求解二叉树的相关问题_分治算法计算二叉树的高度

文章目录

• • 二叉树的前序，中序，后序遍历
    • 求二叉树有多少个节点
    • 求第K层节点的个数
    • 求树的深度
    • 判断单值二叉树

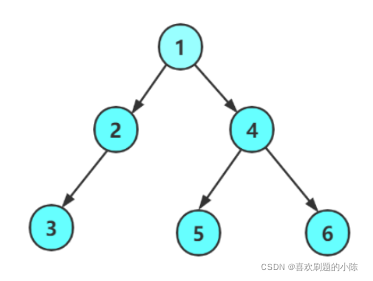
以这个二叉树为例

二叉树构建代码

typedef int BTreeDataType;

typedef struct BTreeNode
{
	BTreeDataType data;
	struct BTreeNode\* left;
	struct BTreeNode\* right;
}BTNode;

BTNode\*  BuyBTreeNode(BTreeDataType x)
{
	BTNode\* node = (BTNode\*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail\n");
		return;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

BTNode\*  test1()
{
	BTNode\* node1 = BuyBTreeNode(1);
	BTNode\* node2 = BuyBTreeNode(2);
	BTNode\* node3 = BuyBTreeNode(3);
	BTNode\* node4 = BuyBTreeNode(4);
	BTNode\* node5 = BuyBTreeNode(5);
	BTNode\* node6 = BuyBTreeNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

二叉树的前序，中序，后序遍历

要理清这三个遍历，一定要对二叉树有一个宏观的概念：
整个看，根是1的二叉树。
分开看，2是根，左子树是3，右子树是NULL ； 3是根，左右是NULL
4是根，左是5，右是6； 5是根，左是NULL，右是NULL。 6是根，左是NULL，右是NULL

前序遍历： 根，左子树，右子树。
所以用递归来遍历就是
1, 2,3 ,NULL,NULL,NULL,4,5,NULL,NULL，6，NULL,NULL

代码：

void PrevOrder(BTNode\* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

大致图解

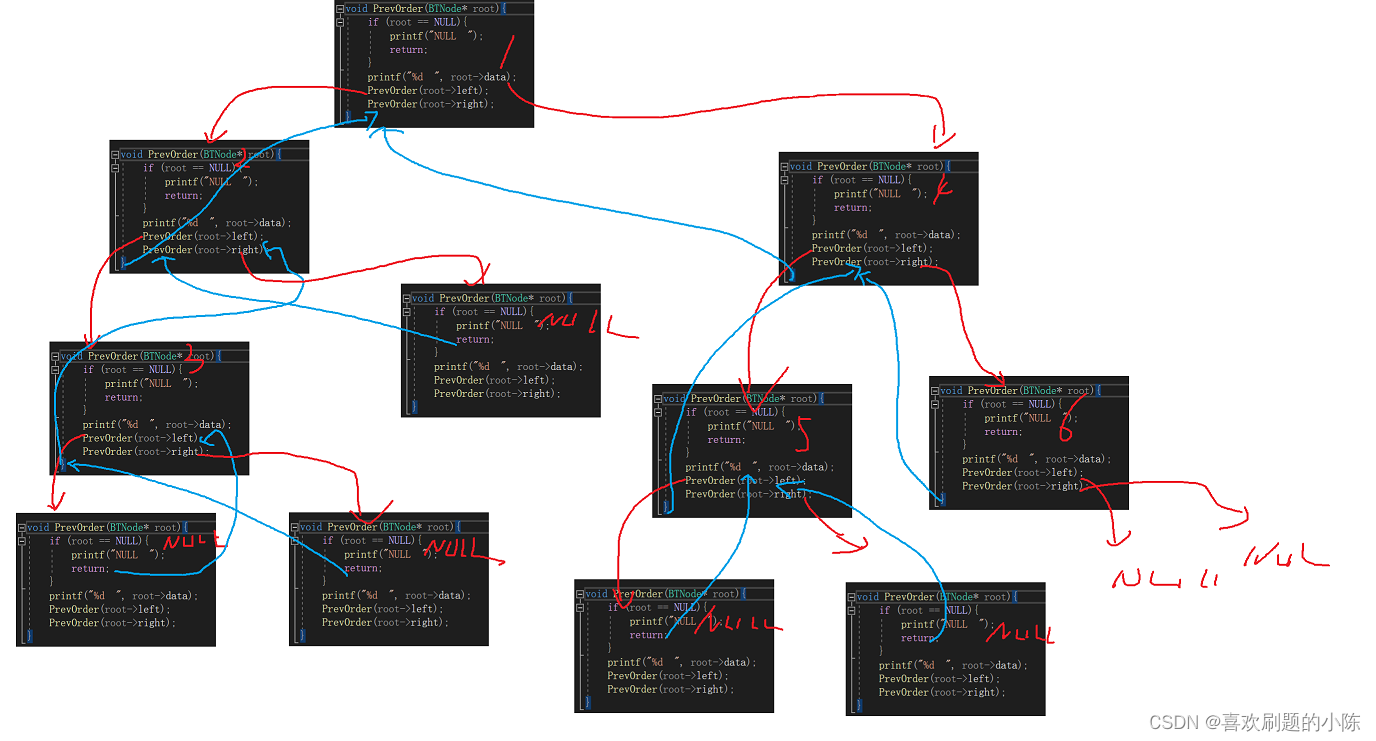
中序遍历：左子树，根，右子树
NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
看代码：

void Inorder(BTNode\* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	Inorder(root->left);
	printf("%d ", root->data);
	Inorder(root->right);
}

后序遍历：左子树，右子树，根

NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1

void BackOrder(BTNode\* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BackOrder(root->left);
	BackOrder(root->right);
	printf("%d ", root->data);
}

求二叉树有多少个节点

方法1，计数的方法（使用全局变量）

int count = 0;
void BTreeSizeNode(BTNode\* root)
{
	if (root == NULL)
	{
		return;
	}
	count++;
	BTreeSizeNode(root->left);
	BTreeSizeNode(root->right);
}

方法二：
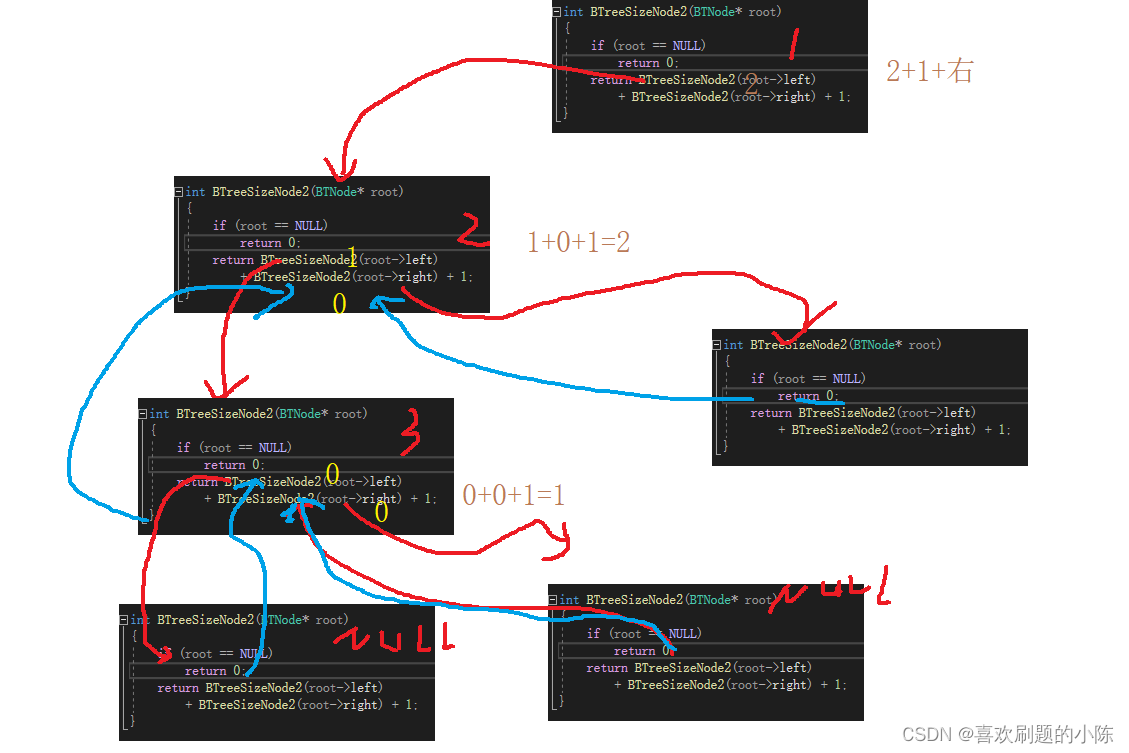
分支法：将问题划分为子问题，再将子问题·划分为更小的子问题，直到不能分为止
要求二叉树的节点个数：就是求每一颗数的左子树+右子树+自己

int BTreeSizeNode2(BTNode\* root)
{
	if (root == NULL)
		return 0;
	 
	//1是自己
	return BTreeSizeNode2(root->left) + BTreeSizeNode2(root->right) + 1;
}

画根为1，左树求解步骤

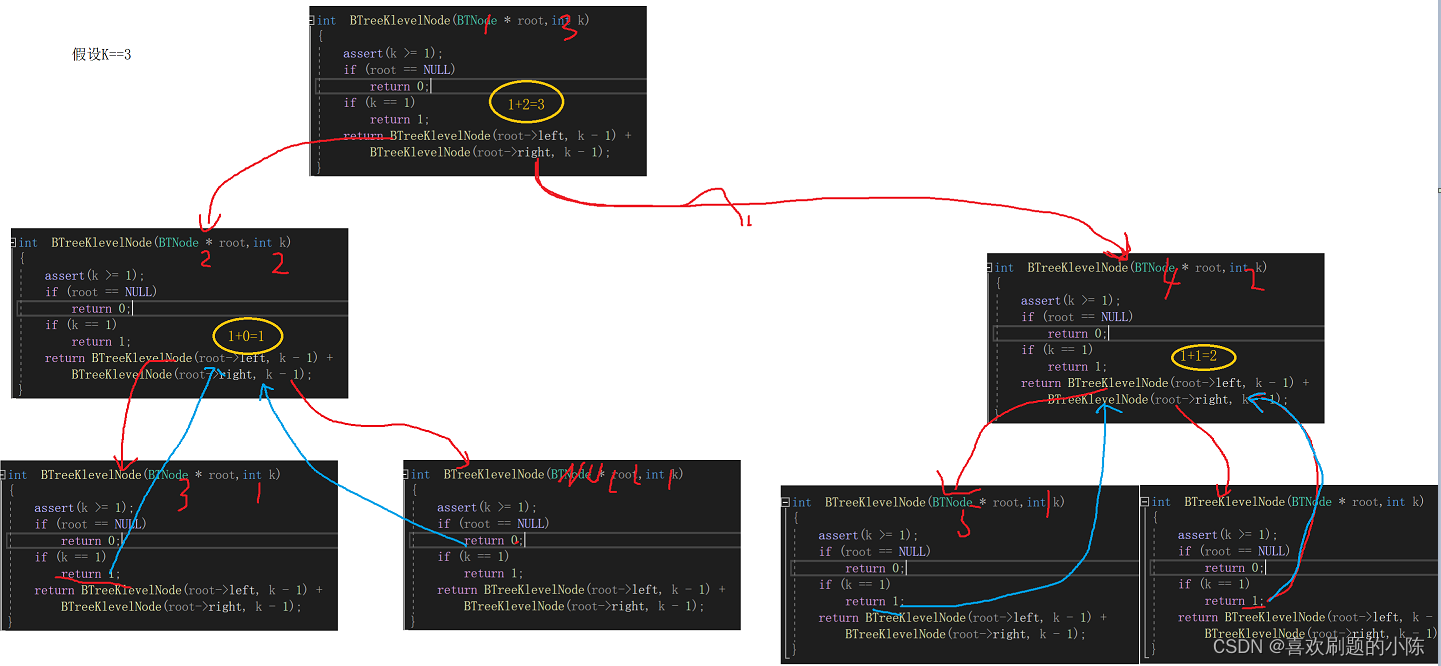
求第K层节点的个数

仍旧使用分治法：
1，rootNULL 返回0
2，k1(第一层)，返回1，
3，第k层=k-1层的左子树和右子树的总和

int  BTreeKlevelNode(BTNode \* root,int k)
{
	assert(k >= 1);
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BTreeKlevelNode(root->left, k - 1) +
		BTreeKlevelNode(root->right, k - 1);
}

粗略的图解

求树的深度