算法入门 - 链表的实现及应用（Java版本）

最新推荐文章于 2025-03-18 22:20:32 发布

原创最新推荐文章于 2025-03-18 22:20:32 发布 · 605 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #链表 #java

节点访问流程：

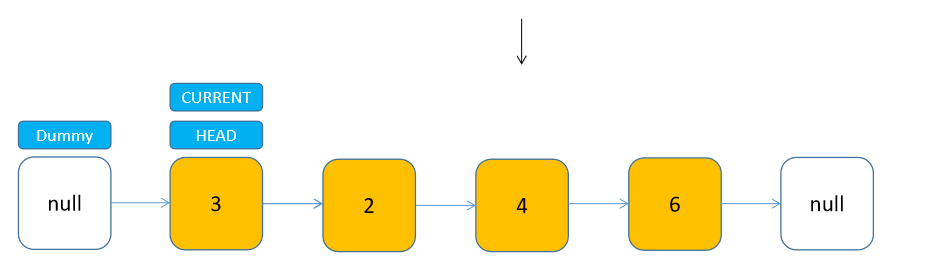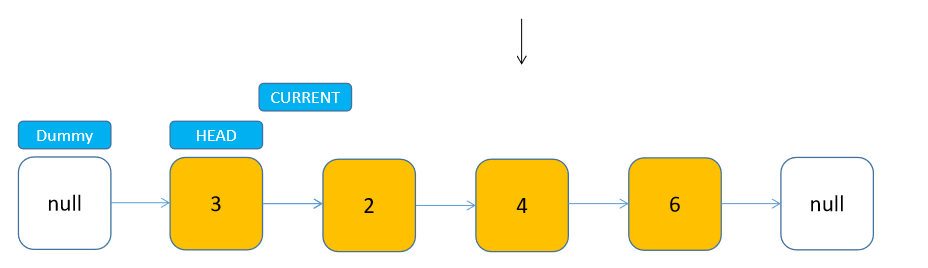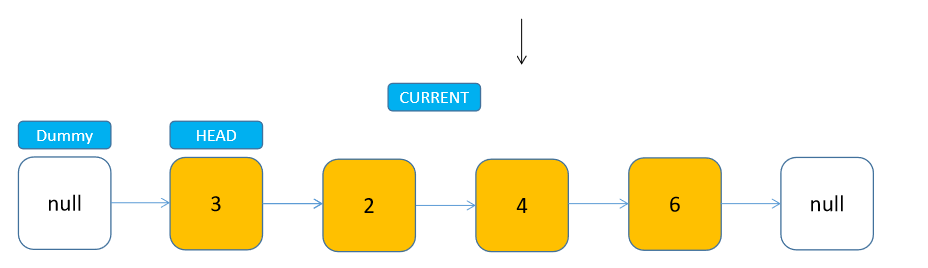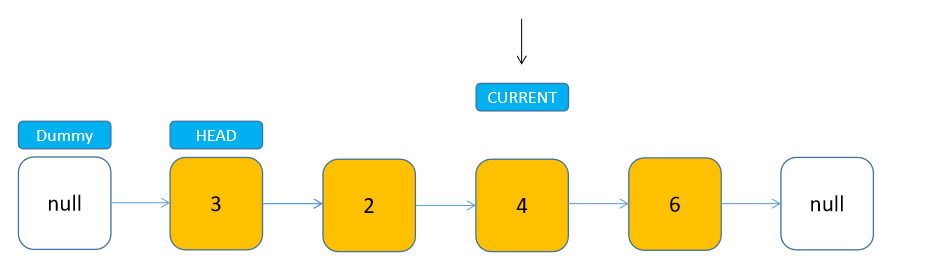
我们之前一直着重在说节点增删的问题，其实访问节点比较简单，只要从头节点开始（dummyHead.next），遍历到索引位置，即可访问到目标节点。

代码实现

基于以上逻辑，我们就可以实现链表了。

package com.algorithm.linkedlist;

import java.lang.String;

// 添加head元素和索引元素分情况处理

public class LinkedList {

// 节点类

private class Node {

public E element; // 节点储存的元素值

public Node next; // 指向的下一个链接节点

public Node(E element, Node node) {

this.element = element;

this.next = node;

}

public Node(E element) {

this.element = element;

this.next = null;

}

public Node() {

}

private Node dummyHead; // 链表dummy节点

private int size; // 链表长度

public LinkedList() {

this.dummyHead = new Node();

this.size = 0;

}

public int getSize() {

return size;

}

public boolean isEmpty() {

return getSize() == 0;

}

// 添加节点

public void add(int index, E element) {

if (index < 0 || index > getSize()) throw new IllegalArgumentException(“index must > 0 and <= size!”);

// prev节点的初始值为dummyHead

Node prev = dummyHead;

// 通过遍历找到prev节点

for (int i = 0; i < index; i++) prev = prev.next;

// 将new Node的next节点指向prev.next，再把prev节点的next指向new Node

prev.next = new Node(element, prev.next);

size++;

}

public void addFirst(E element) {

add(0, element);

}

public void addLast(E element) {

add(getSize(), element);

}

// 移除节点

public E remove(int index) {

if (index < 0 || index >= getSize()) throw new IllegalArgumentException(“index must > 0 and < size!”);

if (getSize() == 0) throw new IllegalArgumentException(“Empty Queue, please enqueue first!”);

// prev节点的初始值为dummyHead

Node prev = dummyHead;

// 通过遍历找到prev节点

for (int i = 0; i < index; i++) prev = prev.next;

// 储存待删除节点

Node delNode = prev.next;

// 跳过delNode

prev.next = delNode.next;

// 待删除节点后接null

delNode.next = null;

size–;

return delNode.element;

}

public E removeFirst() {

return remove(0);

}

public E removeLast() {

return remove(getSize() - 1);

}

// 查找元素所在节点位置

public int search(E element) {

// 从头节点开始遍历

Node current = dummyHead.next;

for (int i = 0; i < getSize(); i++) {

if (element.equals(current.element)) return i;

current = current.next;

}

return -1;

}

// 判断节点元素值

public boolean contains(E element) {

return search(element) != -1;

}

// 获取指定位置元素值

public E get(int index) {

if (index < 0 || index >= getSize()) throw new IllegalArgumentException(“index must > 0 and < size!”);

// 从头节点开始遍历

Node current = dummyHead.next;

for (int i = 0; i < index; i++) current = current.next;

return current.element;

}

public E getFirst() {

return get(0);

}

public E getLast() {

return get(getSize() - 1);

}

// 设置节点元素值

public void set(int index, E element) {

// 从头节点开始遍历

Node current = dummyHead.next;

for (int i = 0; i < index; i++) current = current.next;

current.element = element;

}

@Override

public String toString() {

StringBuilder str = new StringBuilder();

str.append(String.format(“LinkedList: size = %d\n”, getSize()));

Node current = dummyHead.next;

for (int i = 0; i < getSize(); i++) {

str.append(current.element).append(“->”);

current = current.next;

}

str.append(“null”);

return str.toString();

}

// main函数测试

public static void main(String[] args) {

LinkedList linkedList = new LinkedList<>();

for (int i = 0; i < 5; i++) {

linkedList.add(i, i);

System.out.println(linkedList);

}

// 删除首尾节点

linkedList.removeFirst();

linkedList.removeLast();

System.out.println(linkedList);

}

输出内容：

LinkedList: size = 1

0->null

LinkedList: size = 2

0->1->null

LinkedList: size = 3

0->1->2->null

LinkedList: size = 4

0->1->2->3->null

LinkedList: size = 5

0->1->2->3->4->null

LinkedList: size = 3

1->2->3->null

使用链表实现栈

实现了链表后，我们仿照之前的动态数组，也实现一下栈和队列这两种较基础的数据结构。如果需要了解栈和队列，可以看之前的这篇文章。

在写代码前，我们先来分析一下如何实现。栈是一种后进先出的结构，而通过上面对链表的学习，可以发现链表的 head 头节点位置与栈的栈顶非常相似，节点可以通过头节点直接进入链表，也可以直接从头节点脱离链表，而且这两种操作的时间复杂度都是 O(1) 级别的（prev 节点无需移动）。找到了这个特点，就可以很快地利用链表实现栈。

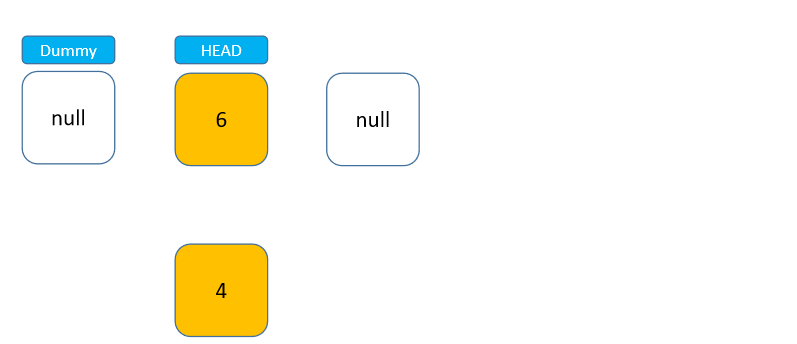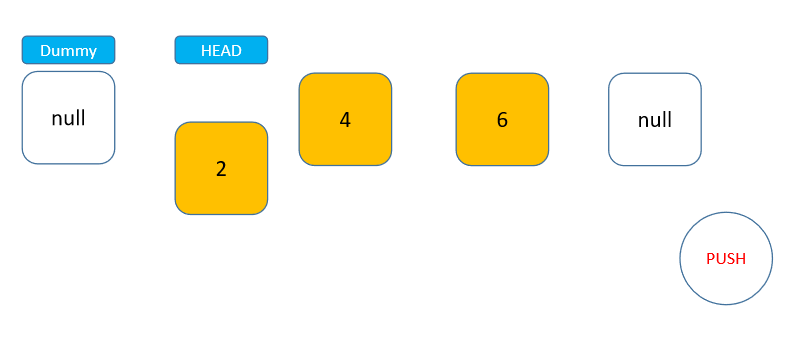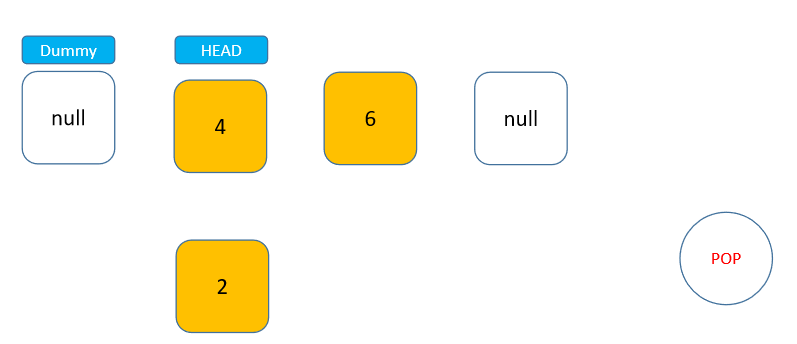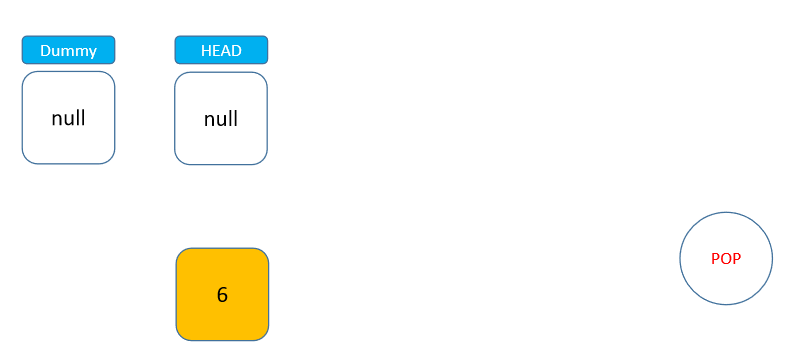
我们还是使用之前的接口实现栈：

package com.algorithm.stack;

public interface Stack {

void push(E element); // 入栈

E pop(); // 出栈

E peek(); // 查看栈顶元素

int getSize(); // 获取栈长度

boolean isEmpty(); // 判断栈是否为空

}

具体实现：

package com.algorithm.stack;

import com.algorithm.linkedlist.LinkedList;

public class LinkedListStack implements Stack{

private LinkedList linkedList; // 使用链表储存栈元素

public LinkedListStack(){

linkedList = new LinkedList<>();

}

// 把链表头作为栈顶，始终对链表头进行操作

// 入栈

@Override

public void push(E element) {

linkedList.addFirst(element);

}

// 出栈

@Override

public E pop() {

return linkedList.removeFirst();

}

// 查看栈顶元素

@Override

public E peek() {

return linkedList.getFirst();

}

// 查看栈中元素个数

@Override

public int getSize() {

return linkedList.getSize();

}

// 查看栈是否为空

@Override

public boolean isEmpty() {

return linkedList.isEmpty();

}

@Override

public String toString() {

return “Stack: top [” + linkedList + “] tail”;

}

// main函数测试

public static void main(String[] args) {

LinkedListStack stack = new LinkedListStack<>();

for (int i=0;i<5;i++){

stack.push(i);

System.out.println(stack);

}

stack.pop();

System.out.println(stack);

}

输出结果：

Stack: top [0->null] tail

Stack: top [1->0->null] tail

Stack: top [2->1->0->null] tail

Stack: top [3->2->1->0->null] tail

Stack: top [4->3->2->1->0->null] tail

Stack: top [3->2->1->0->null] tail

##数组栈VS链表栈

截至目前，我们已经通过两种方式实现了栈，接下来不妨对比一下两种实现方式的性能孰高孰低。可以通过出栈和入栈两种操作进行评估：

package com.algorithm.stack;

import java.util.Random;

public class PerformanceTest {

public static double testStack(Stack stack, int testNum){

// 起始时间

long startTime = System.nanoTime();

// 使用随机数测试

Random random = new Random();

// 入栈测试

for (int i=0;i<testNum;i++) stack.push(random.nextInt(Integer.MAX_VALUE));

// 出栈测试

for (int i=0;i<testNum;i++) stack.pop();

// 结束时间

long endTime = System.nanoTime();

// 返回测试时长

return (endTime - startTime) / 1000000000.0;

}

public static void main(String[] args) {

// 数组栈

ArrayStack arrayStack = new ArrayStack<>();

double arrayTime = testStack(arrayStack, 1000000);

System.out.println("ArrayStack: " + arrayTime);

// 链表栈

LinkedListStack linkedListStack = new LinkedListStack<>();

double linkedTIme = testStack(linkedListStack, 1000000);

System.out.println("LinkedListStack: " + linkedTIme);

}

输出结果：

// testNum = 10万次的测试结果

ArrayStack: 0.0167257

LinkedListStack: 0.0120104

// testNum = 100万次的测试结果

ArrayStack: 0.0509282

LinkedListStack: 0.2121052

第一次使用10万个随机数进行测试时，两者的性能差不多，链表似乎还有小小的优势；而当使用100万个数测试时，链表要明显慢于数组。原因是链表在添加节点的过程中，需要不断地new一个新的节点，而这个new的过程需要寻找新的地址，所以随着次数的增大，耗时变得越来越明显。而数组是先统一申请一批，满了再继续通过resize申请（个数根据数组长度）。但是如果先执行链表，后执行数组，又会出现不同的结果：

public class PerformanceTest {

… …

public static void main(String[] args) {

// 链表栈

LinkedListStack linkedListStack = new LinkedListStack<>();

double linkedTime = testStack(linkedListStack, 1000000);

System.out.println("LinkedListStack: " + linkedTime);

// 数组栈

ArrayStack arrayStack = new ArrayStack<>();

double arrayTime = testStack(arrayStack, 1000000);

System.out.println("ArrayStack: " + arrayTime);

}

输出结果：

LinkedListStack: 0.0368811

ArrayStack: 0.054051

这下链表又比数组快了😂！猜想应该是先跑链表时，空闲空间比较多，找新地址的开销还不大。但是如果在数组已经占用了100万个地址的情况下，再寻找地址就没那么容易了。

使用链表实现队列

实现了栈，再来看队列。队列是一种先进先出的结构，对应到链表，可以使用链表的 head 头节点模拟出队操作（O(1)的时间复杂度）。如果知道了链表尾部的位置，就可以通过从链表尾部添加节点来模拟入队操作，并且这个操作的时间复杂度也是 O(1)。所以我们要再多维护一个 tail 节点，意味着我们要对刚才的链表稍作调整。

同样使用之前的队列接口进行实现：

package com.algorithm.queue;

public interface Queue {

void enqueue(E element); // 入队

E dequeue(); // 出队

E getFront(); // 获取队首元素

int getSize(); // 获取队列长度

boolean isEmpty(); // 判断队列是否为空

}

具体实现：

package com.algorithm.queue;

import java.lang.String;