3.1 矩阵的分解
3.2 矩阵的变换
0 主要内容
矩阵的行列式、秩与迹及特征值分析
矩阵的逆与线性方程组求解
矩阵的分解与变换
1 矩阵的行列式、秩与迹****及特征值分析
1.1 矩阵的行列式
运算符 : det( )
注意 :用于求方阵的行列式值
1.2 矩阵的秩
矩阵的秩是矩阵的列向量组(或行向量组) 的任一极大线性无关组所含向量的个数。
运算符 : rank( )
1.3 矩阵的迹
矩阵的迹等于矩阵主对角线元素的总和。也等于矩阵特征值的总和。
运算符 : trace( )
注意 :要求矩阵是方阵
1.4 矩阵的特征值分析
E=eig(A ):
求矩阵A的全部特征值,并构成向量E
[V,D]=eig(A ):
求矩阵 A 的全部特征值,构成对角矩阵D ;求 A 的特征向量构成列向量V 。
A=[1, - 2,3;2,3,1;3, - 1, - 1]
B=det(A)
C=rank(A)
D=trace(A)
E=eig(A)
[V,D]=eig(A)
A1=[1,2,3;4,5,6]
B1=det(A1)
C1=trace(A1)
2 矩阵的逆与线性方程组求解
2.1 矩阵的逆
inv( )
用于求满秩方阵的逆
pinv( ) 用于求不是方阵或非满秩方阵的
逆—— 伪逆
如果 ABA=A , BAB=B ,则称 B 为 A 的
伪逆,或广义逆矩阵。
2.2 线性方程组求解
AX=B X=
)*B
X = inv ( A )* B
X = inv(A)*B= A\ B (矩阵左除)
3 矩阵的分解与变换
3.1 矩阵的分解
三角分解(方阵): [l,u]=lu(a)
正交分解: [q,r]=qr(a)
a(n,m)
q : n 阶正交方阵
r :与 a 同阶的上三角矩阵
奇异值分解: [u,s,v]=svd(a)
u : n 阶正交方阵
s : n × m 阶的对角阵,对角线元素为 a
的奇异值,长度为n、 m 的较小者
v : m 阶正交方阵
3.2 矩阵的变换
矩阵的共轭转置:’
矩阵的共轭: conj
矩阵的转置: conj’
复数矩阵的赋值
对元素逐个赋值:
z=[1+2i,3+4i;5+6i,7+8i]
对实部和虚部矩阵分别赋值:




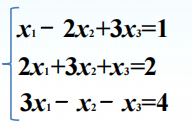
















 1925
1925

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








