【剑斩OFFER】算法的暴力美学——在排序数组中查找元素的第一个和最后一个位置-优快云博客

一、题目描述

二、算法原理

我们可以分为两步来：

①找3的最左端的下标：

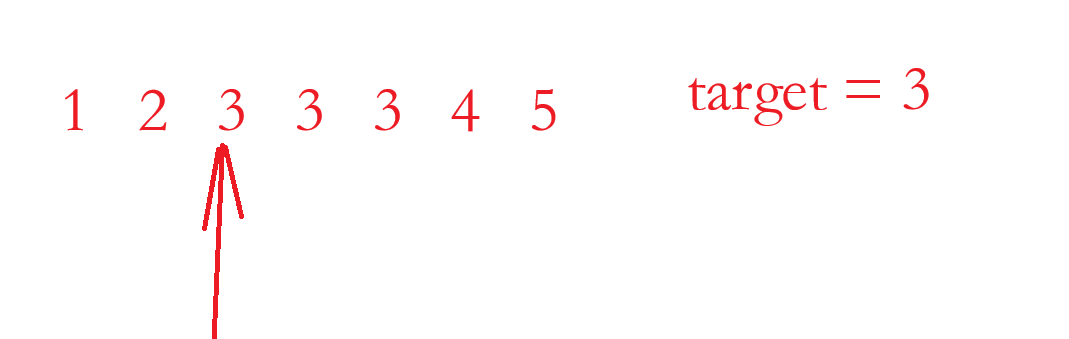
此时这个数组就具有二段性：

1）nums[ mid ] >= target；大于和等于是归为一种的，因为等于时不代表着来到3的最左端；当大于等于时，此时 right = mid ，让 right 移动到 mid ，为什么不是移动到 mid -1 呢？因为 mid 有可能是 3 的最左端。

2）nums[ mid ] < target；此时 left = mid + 1，让 left 移动到 mid + 1 哪里就行。

细节处理：

1、循环条件：left < right

为什么不是 left <= right 呢？

因为当 left == right 时，就是最终答案，无需判断；如果判断就会进入死循环；

为什么当 left == right 时，就是最终答案：

第一种情况：有结果：就是这个数组有3数字：

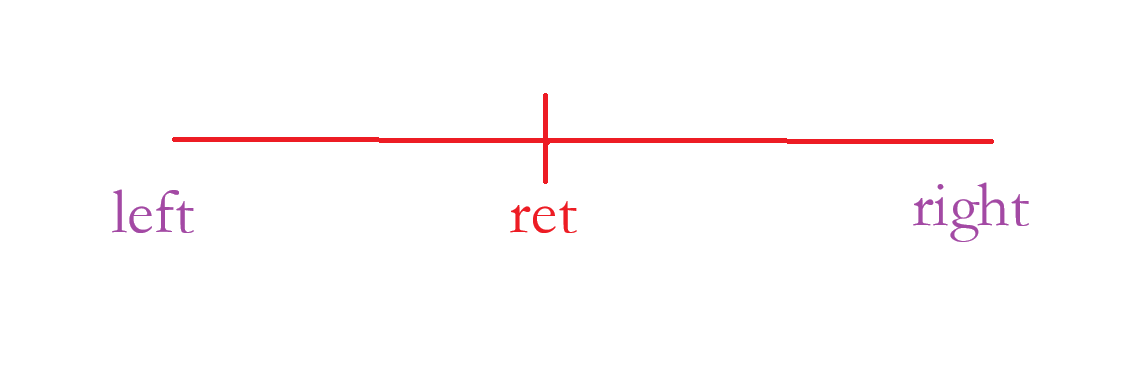
那么根据二段性的条件来看：

当 nums[ mid ]< target 时，right 会逐渐移动到 ret 哪里去，最终移动到 ret ，不会移动超过 ret。注：ret 是 target 的最左边的下标；

当 nums[ mid ] >= target 时，left 会向 ret 靠近，最终会移动到 ret 哪里去；

总结：当 left == right 时，就是最终答案；

第二种情况：数组里面的数字全大于 target ；

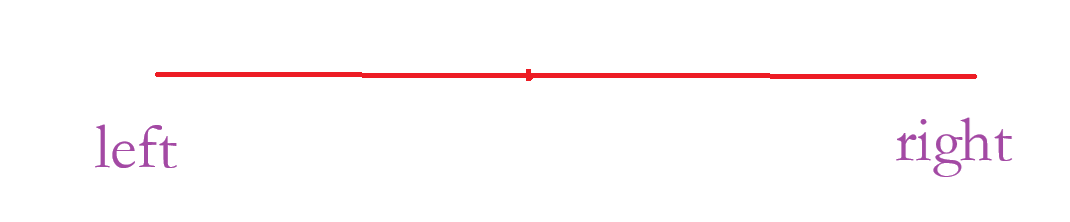
也就是说数组里面数字会命中二段性的 nums[ mid ] >= target，此时 right 会一直向 left 移动，直到移动到 left ；当 left == right 时，因为没有结果，所以我们还要判断一下 nums [ left ] == target；

第三种情况：数组里面的数字全小于 target ；

也就是说数组里面数字会命中二段性的 nums[ mid ] < target，此时 left 会一直向 right 移动，直到移动到 right ；当 left == right 时，因为没有结果，所以我们还要判断一下 nums [ left ] == target；

问题：为什么当 left == right 时，判断就会进入死循环：

进入死循环的情况只有一种：这个数组里面的数字有3：

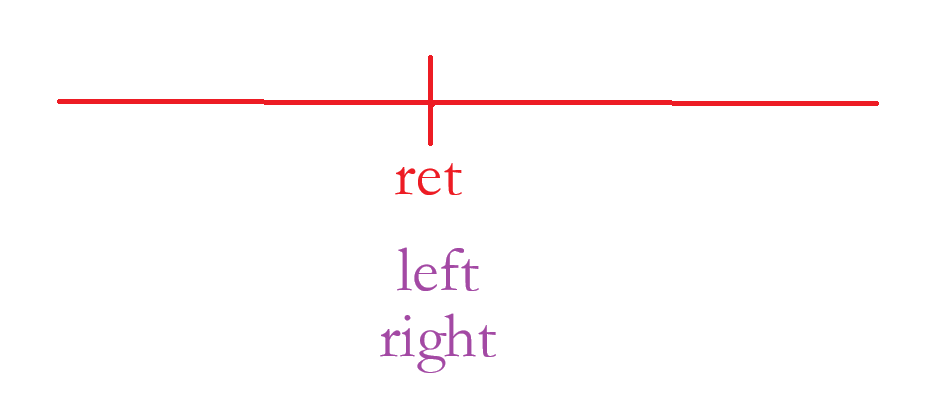
当 left == right 时，我们还循环判断，此时就会命中二段性的条件：nums[ mid ] >= target ，此时 left 和 right 的中点就是还是 left 和 right ，然后不断的进行循环判断。

2、求中点的操作有两种形式：left + (right - left ）/2 和 left + (right - left + 1)/2

这两中形式只有当数组里面的数字的个数是偶数时，left + (right - left)/2 是偏左边的那个的：

而 left + ( right - left + 1) 是偏右的：

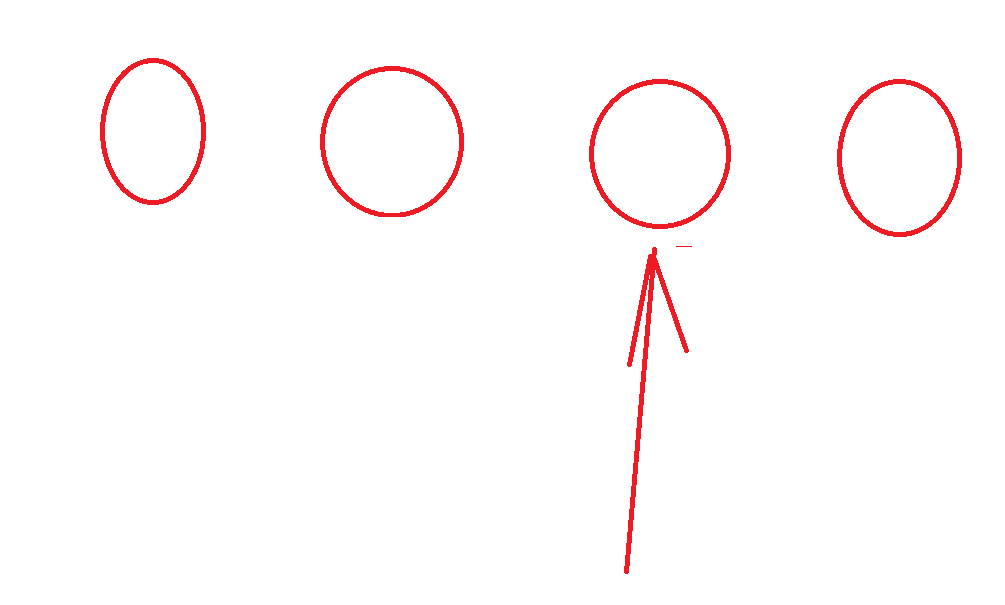
但是我们使用 left - (right - left + 1)/2 的形式时在一种极端的情况下是会进入死循环的：

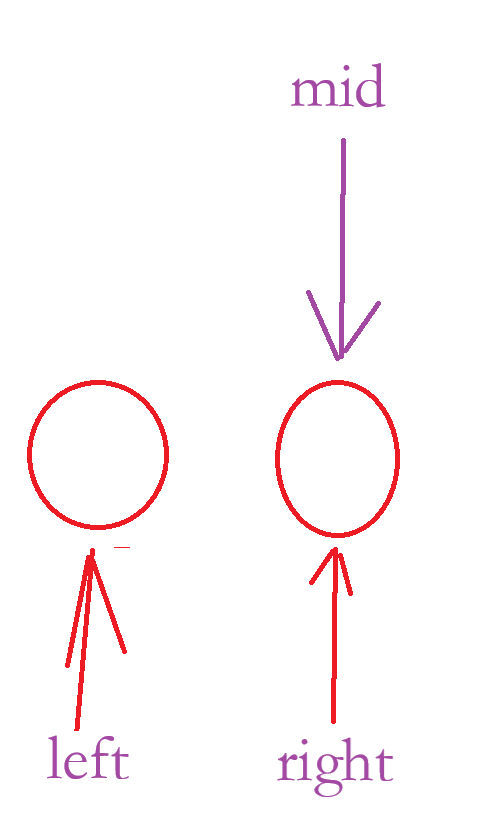
当nums[ mid ] < target 时，left 会跳过right ，结束掉循环，但是当nums[ mid ] >= target 时，right = mid，永远都在死循环。

那么为什么 left + (right - left)/2 不会进入到死循环呢？

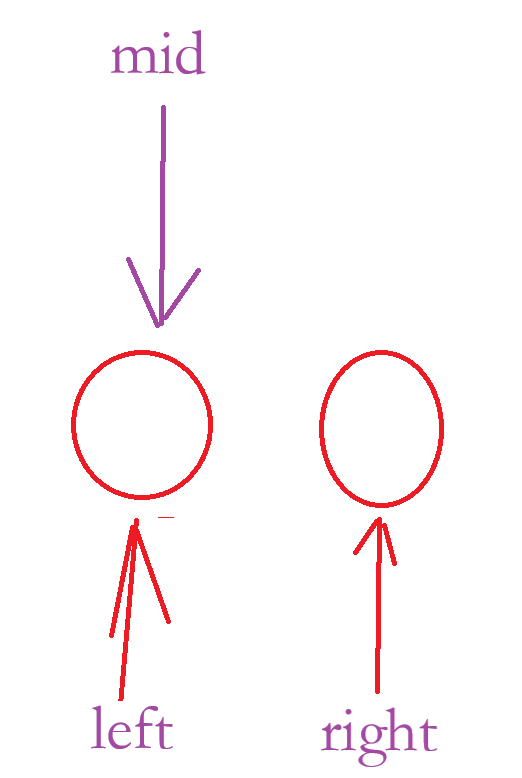
答：当 nums[ mid] >= target 时，right = mid，会结束循环；当 nums[ mid ] < target 时，left = mid + 1 就会 left = right ，结束循环。

总之我们使用 left + (right - left)/2 来求中点操作就行。

②找3的最右端点

既然是找 3 的最右端点，我们就要从3的最右端点进行分割：

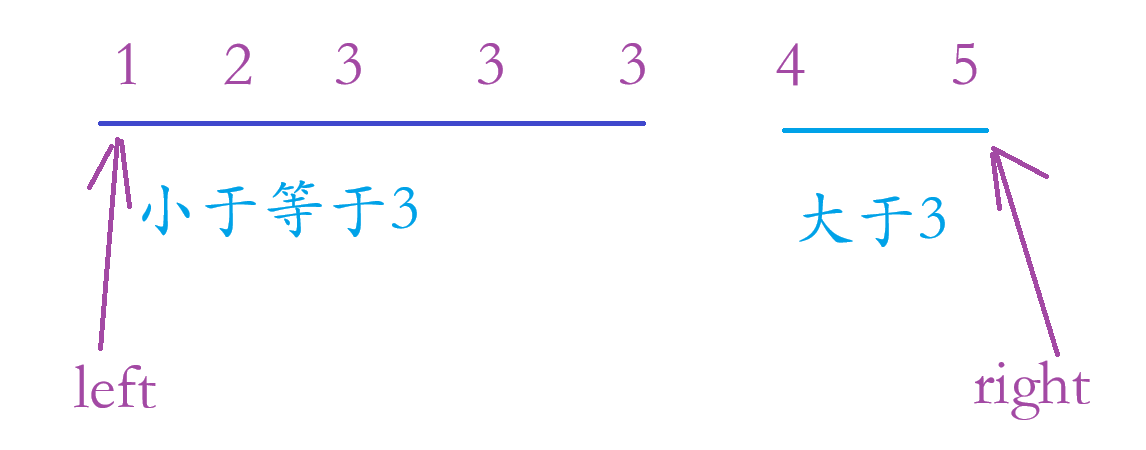
当我们中心点落于小于等于3的区间，我们要移动 left，既：left = mid；为什么？

答：我们不知道 mid 的具体位置，当 mid 指向第23个3时如果此时我们把 left 移动到 mid 左边此时就错过3的最右端点了，如果 left 移动到 mid 的前面此时本来就 mid 的就是正确答案，我们还移动了，所以我们只能让 left 移动到 mid 那里。

当中心点移动到大于3的区间，我们要移动到 mid - 1那里，为什么？

答：因为 mid 大于3，mid 绝对不等于 3，mid +1 也是如此，所以我们只能往 mid - 1 那里去找正确答案。

细节：

循环条件：left < right，原因和①的一样。

求中点方式：mid = left + (right - left + 1)/2

为什么不用 mid = left + (right - left) /2 的方式来求中点？

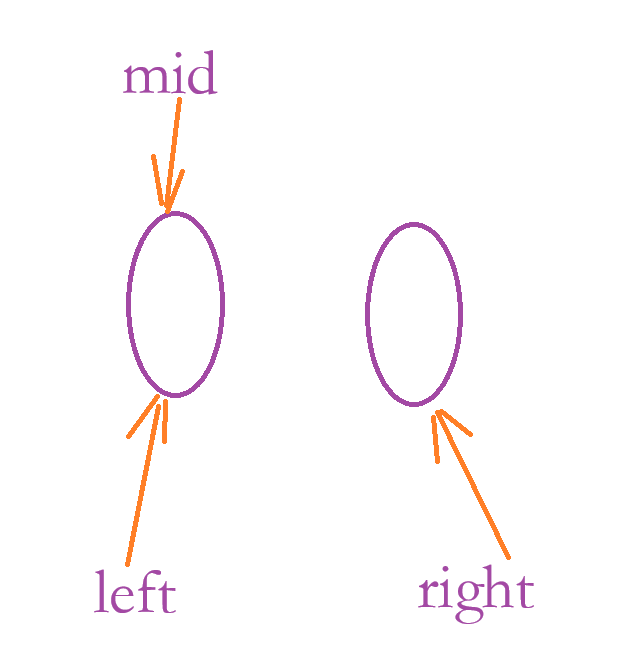
答：当出现这种极端的情况时，使用这种求中点的方式 mid 会落在 left 上，如果 nums[ mid ] <= target，mid = left，此时就会死循环。

三、代码实现

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.size() == 0) return {-1,-1};
        int left = 0,right = nums.size() - 1;
        vector<int> ret;
        while(left < right)//求最左端点
        {
            int mid = left + (right - left)/2;
            if(nums[mid] >= target) right = mid;
            else left = mid + 1;
        }
        if(nums[left] == target) ret.push_back(left);
        else return {-1,-1};


        right = nums.size() - 1;
        while(left < right)//求最右端点
        {
            int mid = left + (right - left + 1)/2;
            if(nums[mid] <= target) left = mid;
            else right = mid - 1;
        }
        ret.push_back(left);//因为执行到这里肯定是找到最左端的，撑死左右端点都一样，所以这里不
        //用再判断 nums[left] 是否等于 target

        return ret;
    }
};

心得：记得判断数组是否为空好吧。

四、二分模板（必学）——查找左端点和右端点的模板

查找左端点：

        while(left < right)//求最左端点
        {
            int mid = left + (right - left)/2;
            if(....) left = mid + 1;
            else right = mid;
        }

记忆小技巧：left 在上，right 在下，查左端点，left 要 +1，right 不变

查找右端点：

        while(left < right)//求最左端点
        {
            int mid = left + (right - left + 1)/2;
            if(....) left = mid;
            else right = mid - 1;
        }

记忆小技巧：left 在上，right 在下，查左端点，left 要不变，right -1