94. 二叉树的中序遍历

原创于 2025-08-18 11:17:04 发布 · 778 阅读

CC 4.0 BY-SA版权

文章标签：

一、题目

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

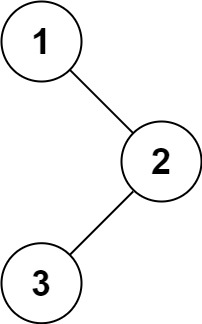
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内

-100 <= Node.val <= 100

二、解题思路（递归算法）

中序遍历是二叉树的三种基础遍历方式之一，核心规则是「左子树 → 根节点 → 右子树」（简称「左→根→右」）

1. 明确问题目标

输入：一棵二叉树的根节点（struct TreeNode* root）。

输出：一个存储节点值的数组，数组元素顺序为二叉树的中序遍历结果（左→根→右）。

要求：数组需通过 malloc 分配内存，由调用者负责释放；同时需要返回数组的长度（通过 returnSize 输出）。

2. 核心思路拆解

（1）确定结果数组的大小

通过getSize函数递归计算二叉树的总节点数

对于空树返回 0，否则返回左子树节点数 + 1（当前节点）+ 右子树节点数

这个大小将作为返回数组的长度

（2）按中序规则遍历并填充数组

中序遍历的顺序是：先遍历左子树，再访问当前节点，最后遍历右子树

使用递归实现inorder函数，通过指针传递索引来记录当前填充位置

递归终止条件：遇到空节点时直接返回

（3）组装主函数

在主函数inorderTraversal中，首先获取树的节点数

根据节点数动态分配内存空间

处理内存分配失败的情况（返回空指针和 0 大小）

初始化索引并调用遍历函数填充数组

返回填充好的结果数组

3.总结

这种实现方式的优点是逻辑清晰，通过先计算大小再分配内存，避免了动态数组扩容的复杂度，同时递归实现的中序遍历也非常直观。需要注意的是，调用者需要在使用完返回的数组后手动释放内存，以避免内存泄漏。

三、代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
//  二叉树节点的标准定义，每个节点包含一个整数值和两个指向左右子节点的指针。
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

// 辅助函数：计算树的节点总数，用于确定结果数组大小
// root 是一个「指向二叉树节点的指针」
int getSize(struct TreeNode* root) {
    if (root == NULL) return 0;
    // 节点总数 = 左子树节点数 + 1（当前节点） + 右子树节点数
    return getSize(root->left) + 1 + getSize(root->right);
}

// 辅助递归函数：执行中序遍历并填充结果数组
// root：当前正在处理的节点（比如根节点、左子节点、右子节点）。
// result：存储遍历结果的数组（所有递归调用都共用这一个数组）。
// index：指向一个整数的指针，记录「当前该往数组的哪个位置存值」（所有递归调用共用这一个索引，用指针才能保证共享）。
void inorder(struct TreeNode* root, int* result, int* index) {
    if (root == NULL) return;  // 空节点直接返回
    
    // 1. 先递归遍历左子树
    inorder(root->left, result, index);
    
    // 2. 再访问当前节点（根节点）
    result[*index] = root->val;
    (*index)++;  // 索引后移
    
    // 3. 最后递归遍历右子树
    inorder(root->right, result, index);
}

// 主函数
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    // 计算节点总数，确定结果数组大小
    *returnSize = getSize(root);
    
    // 分配结果数组内存
    int* result = (int*)malloc(*returnSize * sizeof(int));
    if (result == NULL) {
        *returnSize = 0;
        return NULL;  // 内存分配失败处理
    }
    
    int index = 0;  // 用于记录当前填充到结果数组的位置
    inorder(root, result, &index);  // 调用递归函数
    
    return result;
}

四、总结

本次通过递归算法实现二叉树的中序遍历，整体逻辑清晰且易于理解，核心优势与注意事项可总结如下：

1. 算法核心优势

逻辑直观：严格遵循中序遍历 “左→根→右” 的规则，通过递归自然表达遍历顺序，代码可读性强，符合人类对二叉树遍历的思维习惯。

内存高效：先通过getSize函数计算节点总数，再一次性分配对应大小的数组内存，避免了动态扩容的开销，也无需额外的临时存储结构（如栈的显式使用）。

边界处理完善：针对空树（输入root = []）、单节点树（输入root = [1]）等特殊情况均能正确处理，返回空数组或单个节点值，同时通过判断malloc的返回值处理内存分配失败的场景。

2. 关键技术点回顾

递归的应用：递归是实现二叉树遍历的天然工具。在inorder函数中，通过递归调用自身处理左子树和右子树，将复杂的遍历过程分解为重复的子问题（“处理当前节点的左子树→记录当前节点→处理当前节点的右子树”），简化了代码实现。

指针传递的作用：使用指针index记录数组填充位置，确保所有递归调用共享同一个索引变量，避免了因值传递导致的索引混乱，保证了数组填充的顺序性。

内存管理意识：结果数组通过malloc动态分配，明确要求调用者使用后手动释放内存，避免内存泄漏，符合 C 语言动态内存管理的规范。

3. 适用场景与局限性

适用场景：适用于节点数量较少（如题目中限制的[0, 100]范围）的二叉树遍历，递归深度不会超过节点数，无需担心栈溢出问题，且代码实现简洁。

局限性：对于极端情况下的大型二叉树（如链状结构，递归深度极大），可能会因递归调用栈溢出导致程序崩溃。此时需考虑非递归（迭代）实现（如使用栈模拟递归过程）来规避这一问题。

4. 问题拓展

二叉树的三种基础遍历（前序、中序、后序）核心差异仅在于 “访问根节点” 的时机。若需实现前序遍历（根→左→右）或后序遍历（左→右→根），只需调整inorder函数中 “记录当前节点值” 的位置：

前序遍历：先记录根节点，再遍历左子树，最后遍历右子树；

后序遍历：先遍历左子树，再遍历右子树，最后记录根节点。

通过本次实现，可进一步理解递归在树结构问题中的核心作用 —— 将树的层级结构转化为递归的子问题，从而高效解决遍历、搜索、计算等基础任务。