opencv 霍夫直线变换的原理

对于一条直线（不垂直于x轴的直线），都可以用y=k x+b来表示，此时，x和y是横纵坐标，k和b是一个固定参数。当我们换一种方式来看待这个式子，我们就可以得到：

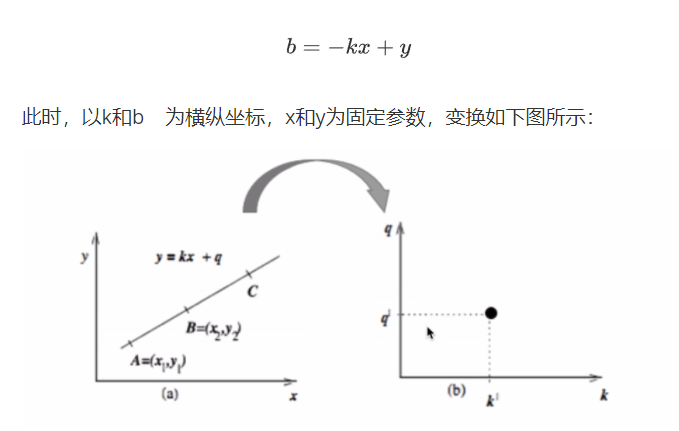
从上图可以看出，在直角坐标系下的一个直线，在变换后的空间中仅仅表示为一点，对于变换后的空间，我们称其为霍夫空间。也就是说，直角坐标系下的一条直线对应了霍夫空间中的一个点。类似的，霍夫空间中的一条直线也对应了直角坐标系中的一个点，如下图所示：

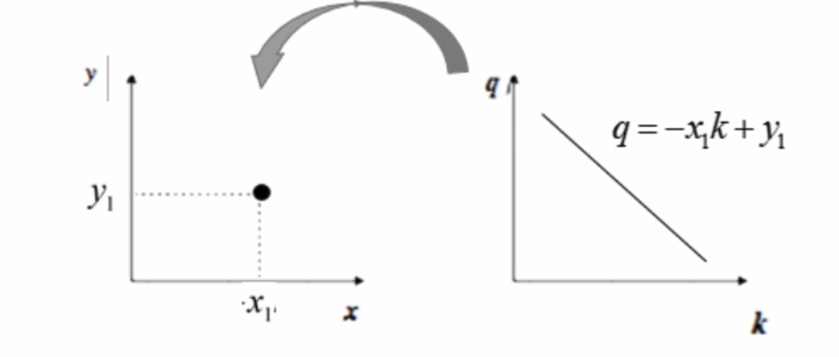
那么对于一个二值化后的图形来说，其中的每一个目标像素点（这里假设目标像素点为白色像素点）都对应了霍夫空间的一条直线，当霍夫空间中有两条直线相交时，就代表了直角坐标系中某两个点所构成的直线。而当霍夫空间中有很多条线相交于一点时，说明直角坐标系中有很多点能构成一条直线，也就意味着这些点共线，因此我们就可以通过检测霍夫空间中有最多直线相交的交点来找到直角坐标系中的直线。

然而对于x=1这种直线来说，y已经不存在了，那么就没办法使用上面的方法进行检测了，为了解决这个问题，我们就将直角坐标系转化为极坐标系，然后通过极坐标系与霍夫空间进行相互转化。

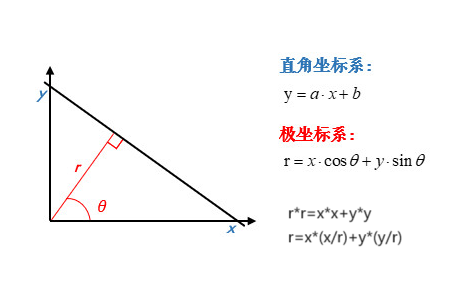
在极坐标系下是一样的，极坐标中的点对于霍夫空间中的线，霍夫空间中的点对应极坐标中的直线。并且此时的霍夫空间不再是以k为横轴、b为纵轴，而是以为θ横轴、ρ(上图中的r)为纵轴。上面的公式中，x、y是直线上某点的横纵坐标（直角坐标系下的横纵坐标），和是极坐标下的坐标，因此我们只要知道某点的x和y的坐标，就可以得到一个关于θ-ρ的表达式，如下图所示：

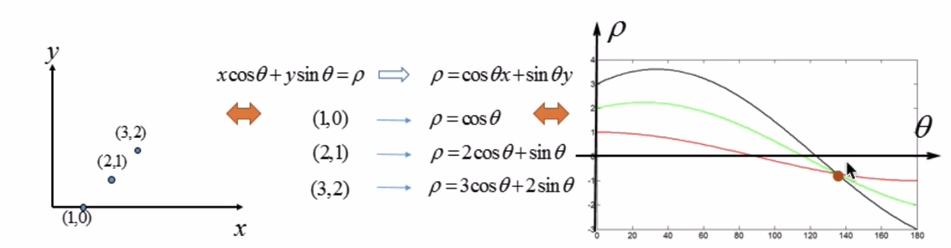
根据上图，霍夫空间在极坐标系下，一点可以产生一条三角函数曲线，而多条这样的曲线可能会相交于同一点。因此，我们可以通过设定一个阈值，来检测霍夫空间中的三角函数曲线相交的次数。如果一个交点的三角函数曲线相交次数超过阈值，那么这个交点所代表的直线就可能是我们寻找的目标直线。