前言
在之前文章的练习题当中,我们初步探讨了环形链表的问题,通过代码来实现判断一个链表是否是代环的,那么本篇文章就来继续深入探讨有关环形链表的问题。
( 之前的文章——【点我跳转】)
1. 判断链表是否带环
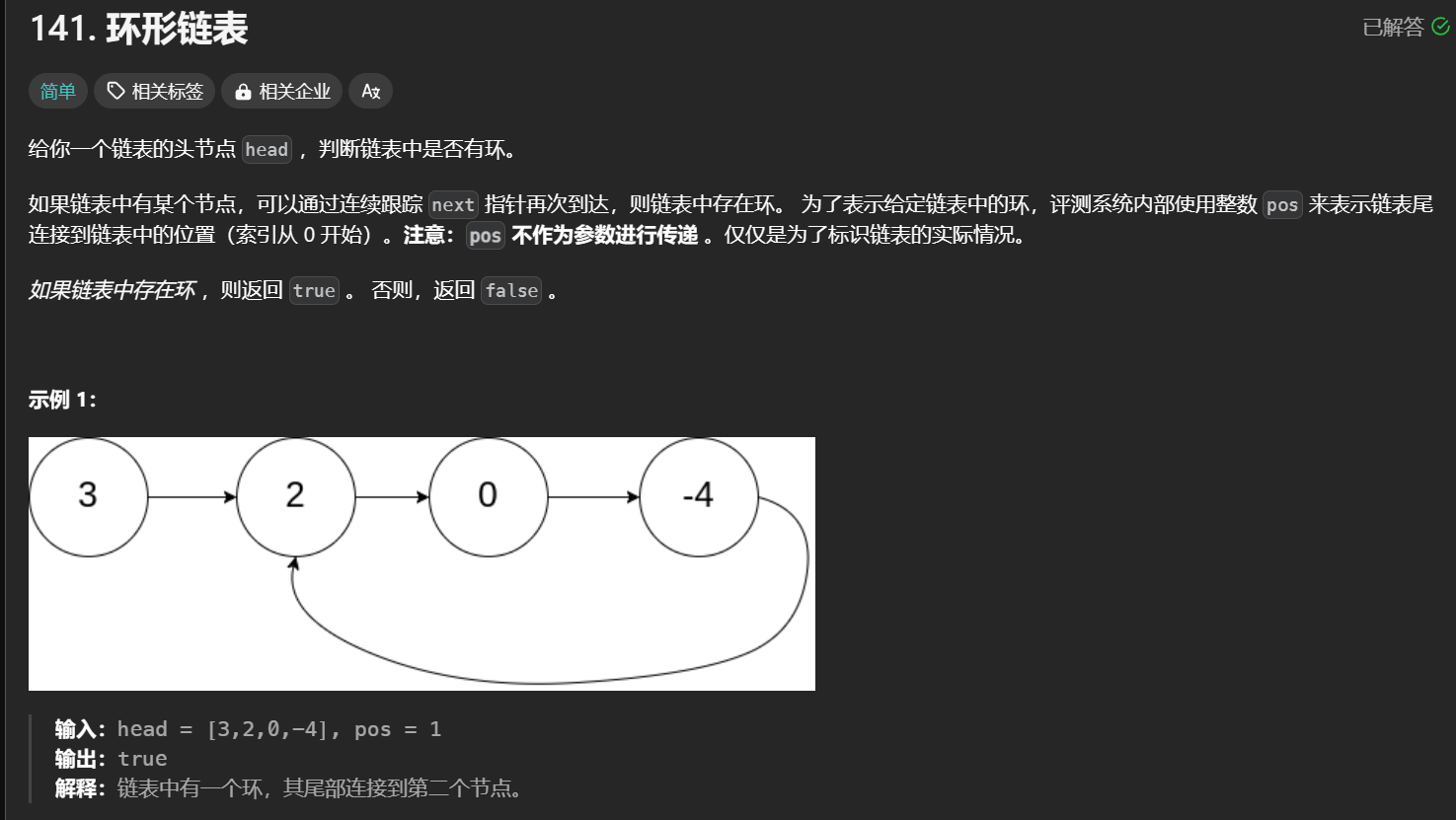
leetcode 141. 环形链表
方法 1:快慢指针
如果说一个链表有环,那么我定义一个指针沿着链表走的话是永远走不出去的,既然这样,我可以定义两个指针,一个快指针一个慢指针,快指针一次走两,慢指针一次走一步,如果它们相遇了,说明链表带环。反之如果快指针走出去了,说明不带环。
bool hasCycle(struct ListNode *head) {
struct ListNode* fast = head, *slow = head;
while(fast && fast->next){
fast = fast->next->next;
slow = slow->next;
if(fast == slow) return true;
}
return false;
}
2. *环形链表衍生问题
- fast \operatorname{fast} fast 和 slow \operatorname{slow} slow 会不会在环中错过,永远不会相遇?
结论: fast \operatorname{fast} fast 和 slow \operatorname{slow} slow 一定会相遇,不会错过
这个比较好理解,它们相对速度为 1 1 1,把 slow \operatorname{slow} slow 看作是 ”静止“ 的那么 fast \operatorname{fast} fast 就一定会追上 slow \operatorname{slow} slow。
- 如果 fast \operatorname{fast} fast 一次走 n n n 步 ( n > 2 ) (n>2) (n>2),可不可行?
结论: fast \operatorname{fast} fast 一次走 n n n 步, n > 2 n>2 n>2 时不一定会相遇
相对速度为 n − 1 n-1 n−1(甚至可以是 n − m n-m n−m),但是这样就不一定能追上了,这还和环的大小 C C C 以及进环之前的距离大小有关系,下面我们来详细的讨论一下,以走 3 3 3 步为例:
如果说当 slow \operatorname{slow} slow 进环时 fast \operatorname{fast} fast 和 slow \operatorname{slow} slow 之间的距离是 N N N,由于此时的相对速度是 2 2 2,那么 fast \operatorname{fast} fast 和 slow \operatorname{slow} slow 之间的距离就会以每次减 2 2 2 的趋势缩小,即 N − 2 − 2 ⋯ N-2-2\cdots N−2−2⋯ 。不难发现,当 N N N 是偶数的时候,这个距离一定会减到 0 0 0,而当 N N N 是个奇数的时候,它们将会在 “第一轮” 的追及中错过。那现在就算是错过了一轮了,这时候它们的距离将会变成 C − 1 C-1 C−1, C C C 是环的大小。现在这个距离 C − 1 C-1 C−1 又可以看作是我们之前讨论的 N N N,如果说 C − 1 C-1 C−1 是一个偶数,即 N N N 为偶数的时候,由前可知,它们将会在 “第二轮” 的追及中相遇。反之,如果这个 C − 1 C-1 C−1 是一个奇数,那么它们就会陷入一个错过的死循环,永远无法相遇。
同理,走 n n n 步的时候就讨论的不是奇偶的问题了,就要讨论是不是 n − 1 n-1 n−1 的倍数的问题了。
- 如何找到环的入口点呢?
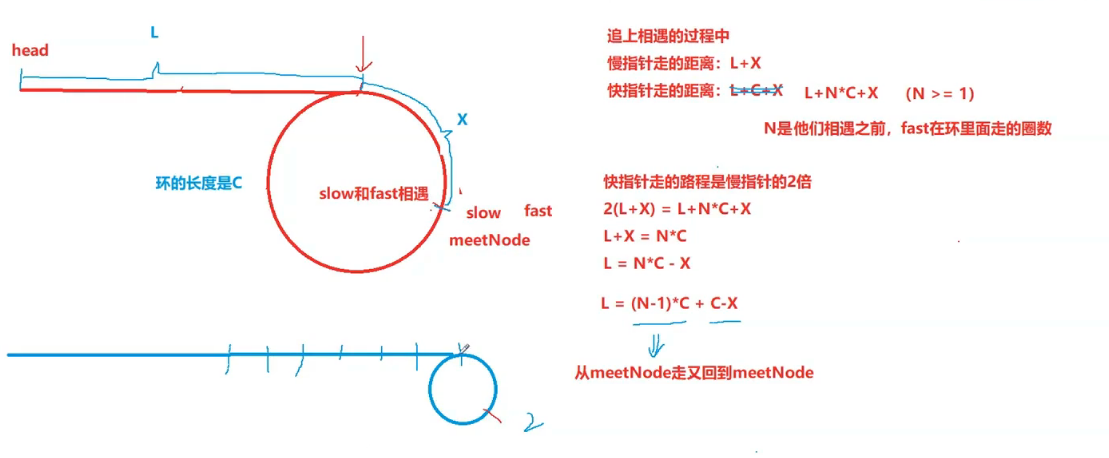
结论:一个指针从相遇点走,一个指针从表头开始走,它们就会在环的入口点相遇
假设 slow \operatorname{slow} slow 从环入口走到相遇点的距离是 x x x,进环之前走的距离是 L L L,那么在第一次相遇时, slow \operatorname{slow} slow 所走的距离为 L + x L+x L+x, fast \operatorname{fast} fast 所走的距离是 L + n ⋅ C + x L+n\cdot C+x L+n⋅C+x 。( 注意 fast \operatorname{fast} fast 所走的不一定是 L + C + x L+C+x L+C+x )
fast
\operatorname{fast}
fast 走的路程是
slow
\operatorname{slow}
slow 走的两倍,于是有
2
(
L
+
x
)
=
L
+
n
⋅
C
+
x
⇓
L
=
n
⋅
C
−
x
2(L+x)=L+n\cdot C+x\\ \Downarrow\\ L=n\cdot C-x
2(L+x)=L+n⋅C+x⇓L=n⋅C−x
OK,接下来我们再进行一个变形得
L
=
(
n
−
1
)
C
+
(
C
−
x
)
L=(n-1)C+(C-x)
L=(n−1)C+(C−x)
等式左边是走到环入口前的一段距离
L
L
L,而等式右边
(
n
−
1
)
C
(n-1)C
(n−1)C,是一个环的长度的整数倍,相当于从相遇点绕圈走又回到相遇点,
(
C
−
x
)
(C-x)
(C−x) 刚好是从相遇点走到环入口点的位置。两边相等,说明两指针分别从头和相遇点开始走的话最终一定会在环的入口点处相遇。
3. 找出环的入口点
leetcode 142. 环形链表Ⅱ
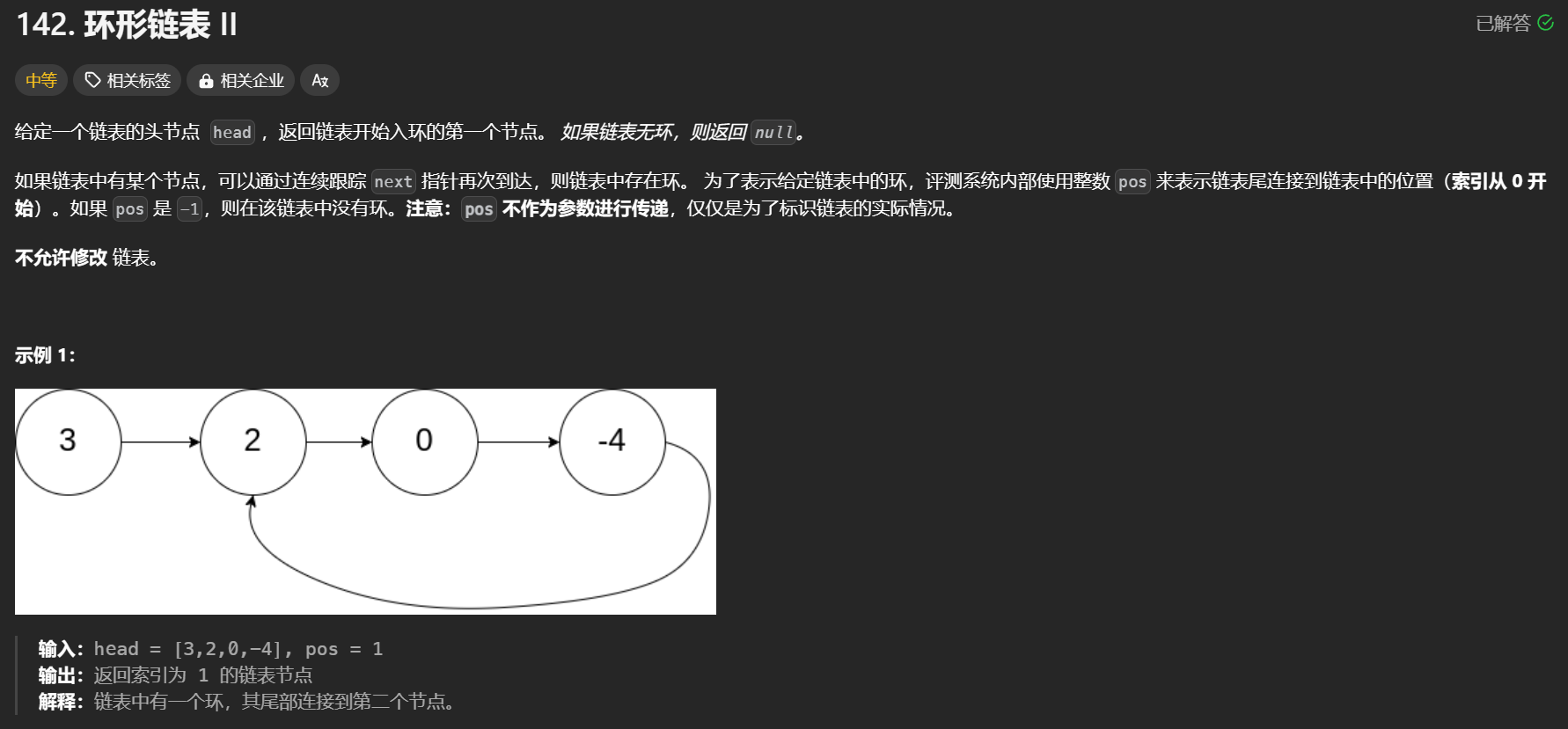
方法 1:快慢指针(具体数学推理过程见上)
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode *slow = head, *fast = head;
while(fast && fast->next){
fast = fast->next->next;
slow = slow->next;
if(fast == slow){
// 快慢指针相遇了
struct ListNode* meetNode = slow;
while(meetNode != head){ // 一个指针从相遇点走,一个指针从表头开始走
meetNode = meetNode->next;
head = head->next;
}
return meetNode; // 相遇的地方就是环的入口
}
}
return NULL;
}






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








