【AI大模型面试真题】为什么NLP用Layernorm而不是batchnorm？

为什么NLP用Layernorm而不是batchnorm？

面试题

为什么NLP用Layernorm而不是batchnorm？

理论基础

什么是 批量归一化（Batch Normalization，BN）？

• 核心原理： BN在每一层的训练过程中，对输入的激活值在小批量（batch）内进行归一化。

• 计算步骤：

1. 计算均值和方差：对于给定的批量输入，计算每个神经元的均值μ 和方差σ;

2. 归一化：使用计算得到的均值和方差，对输入进行标准化处理，使其均值为0，方差为1。

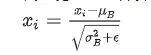
1. 缩放和平移：引入可学习的参数 γ 和 β，对标准化后的数据进行缩放和平移，以增加模型表达能力。

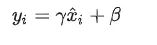
简单例子： 假设我们有一个批量大小为2的输入 [2, 4]。我们计算其均值 μB=3 和方差 σ。归一化后得到 [−1,1][-1, 1][−1,1]。然后应用缩放和平移参数，例如 γ=2 和 β=1，最后得到 [−1×2+1,1×2+1]=[−1,3]。

• 应用：主要用于卷积神经网络中，通过对 mini-batch 的每个维度进行标准化，减少内部协变量偏移，提高训练的稳定性。

什么是 层归一化（Layer Normalization，LN）？

• 核心原理： LN不在批量维度上进行归一化，而是在特征维度上进行归一化。其步骤如下：

• 计算步骤：

1. 计算均值和方差：对于给定输入的每一层，计算每个样本特征维度的均值μ 和方差σ;

2. 归一化：使用计算得到的均值和方差，对输入进行标准化处理，使其均值为0，方差为1。

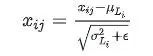
1. 缩放和平移：引入可学习的参数 γ 和 β，对标准化后的数据进行缩放和平移

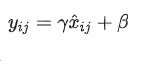
简单例子： 假设我们有一个输入向量 [1, 2, 3]。我们计算其均值μL=2 和方差 σ 。归一化后得到 [-1, 0, 1]。然后应用缩放和平移参数，例如 γ=1 和 β=0，最后得到 [-1, 0, 1]。

• 应用：LayerNorm (Layer Normalization) 主要用于 RNN 和 Transformer 等序列模型中，它对整个层进行标准化，独立于 mini-batch，确保在不同时间步和序列长度下具有一致的归一化效果。

为什么NLP用Layernorm而不是batchnorm？

CV中，数据shape为（n：图片数，channel：通道数，H*W：长 * 宽）。

CV中，把channel，通道维视为特征维，如RGB三原色。把一个batch内全部图片，分别对红、绿、蓝计算出了三个均值和标准差。每张图片宽高确定，符合物理实际意义，符合图片数据特点。

NLP中，数据shape为（batch：句子数，seq_len：句子长度，d：词嵌入维度）。

NLP中，如果也像CV一样，把中间的seq_len句子长度维视为特征维，

1. 首先没意义，因为句子不像图片，比如图片计算RGB三原色，还是有实际物理意义，而nlp的文本中每个句子第i个词所在的位置算均值标准差没意义，不同句子第i个词没什么物理意义关系。

2. 没法算，不同句子长度不同，有的句子后面全是padding补齐的0，这些padding位置算norm没法算。

所以NLP中采用layernorm，把第一个batch维视为特征维，针对句子之内算norm，最后输出batch个norm。才符合NLP数据的特点。

最后的最后

感谢你们的阅读和喜欢，我收藏了很多技术干货，可以共享给喜欢我文章的朋友们，如果你肯花时间沉下心去学习，它们一定能帮到你。

因为这个行业不同于其他行业，知识体系实在是过于庞大，知识更新也非常快。作为一个普通人，无法全部学完，所以我们在提升技术的时候，首先需要明确一个目标，然后制定好完整的计划，同时找到好的学习方法，这样才能更快的提升自己。

这份完整版的大模型 AI 学习资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】

大模型知识脑图

为了成为更好的 AI大模型 开发者，这里为大家提供了总的路线图。它的用处就在于，你可以按照上面的知识点去找对应的学习资源，保证自己学得较为全面。

经典书籍阅读

阅读AI大模型经典书籍可以帮助读者提高技术水平，开拓视野，掌握核心技术，提高解决问题的能力，同时也可以借鉴他人的经验。对于想要深入学习AI大模型开发的读者来说，阅读经典书籍是非常有必要的。

实战案例

光学理论是没用的，要学会跟着一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

面试资料

我们学习AI大模型必然是想找到高薪的工作，下面这些面试题都是总结当前最新、最热、最高频的面试题，并且每道题都有详细的答案，面试前刷完这套面试题资料，小小offer，不在话下

640套AI大模型报告合集

这套包含640份报告的合集，涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师，还是对AI大模型感兴趣的爱好者，这套报告合集都将为您提供宝贵的信息和启示。

这份完整版的大模型 AI 学习资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】