【理论+实践】史上最全-论文中常用的图像分割评价指标-附完整代码_分割指标hd95 aorta

“”"
pa = ((s == g).sum()) / g.size
return pa
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
pa = binary_pa(s, g)

是不是就很简单~~~~


![在这里插入图片描述](https://img-blog.csdnimg.cn/20210607185533902.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTQyNjQzNzM=,size_16,color_FFFFFF,t_70#pic_center)  
 这部分还没完。我们继续~~~~~


思考一下，PA很简单，但是，它绝不是最好的指标。  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/20210607190238574.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTQyNjQzNzM=,size_16,color_FFFFFF,t_70)  
 在这个案例中，即使模型什么也没有分割出来，但他的PA = 95%， what？？？


嗯。我们的计算有问题吗？不。完全正确。只是背景类是原始图像的 95%。因此，如果模型将所有像素分类为该类，则 95% 的像素被准确分类，而其他 5% 则没有。


因此，尽管您的准确率高达 95%，但您的模型返回的是完全无用的预测。这是为了说明高像素精度并不总是意味着卓越的分割能力。


这个问题称为类别不平衡。当我们的类极度不平衡时，这意味着一个或一些类在图像中占主导地位，而其他一些类只占图像的一小部分。不幸的是，类不平衡在许多现实世界的数据集中普遍存在，因此不容忽视。


因此，这个指标基本没什么指导意义。


## 2 交并比 IoU


Intersection-Over-Union (IoU)，也称为 Jaccard 指数，是语义分割中最常用的指标之一……这是有充分理由的。IoU 是一个非常简单的指标，非常有效。


### 2.1 理论


简单地说，IoU 是预测分割和标签之间的重叠区域除以预测分割和标签之间的联合区域（两者的交集/两者的并集），如图所示。该指标的范围为 0–1 (0–100%)，其中 0 表示没有重叠，1 表示完全重叠分割。


对于二元分类而言，其计算公式为：


 
 
 
 
 
 I 
 
 
 o 
 
 
 U 
 
 
 = 
 
 
 
 
 ∣ 
 
 
 A 
 
 
 ⋂ 
 
 
 B 
 
 
 ∣ 
 
 
 
 
 ∣ 
 
 
 A 
 
 
 ⋃ 
 
 
 B 
 
 
 ∣ 
 
 
 
 
 = 
 
 
 
 
 T 
 
 
 P 
 
 
 
 
 T 
 
 
 P 
 
 
 + 
 
 
 F 
 
 
 P 
 
 
 + 
 
 
 F 
 
 
 N 
 
 
 
 
 
 IoU = \frac{|A \bigcap B|}{|A \bigcup B|} = \frac{TP}{TP + FP + FN} 
 
 
 IoU=∣A⋃B∣∣A⋂B∣​=TP+FP+FNTP​  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/20210607194016419.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTQyNjQzNzM=,size_16,color_FFFFFF,t_70#pic_center)  
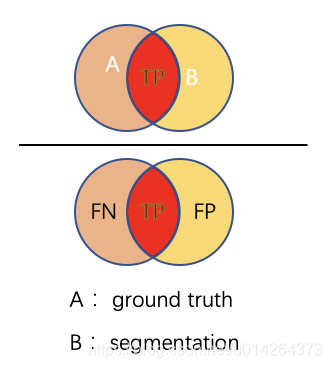
 还是上面那个3 \* 3 的例子，我们来计算一下它的IoU


 
 
 
 
 
 I 
 
 
 o 
 
 
 U 
 
 
 = 
 
 
 
 
 交 
 
 
 集 
 
 
 = 
 
 
 3 
 
 
 
 
 并 
 
 
 集 
 
 
 = 
 
 
 5 
 
 
 
 
 = 
 
 
 
 
 T 
 
 
 P 
 
 
 = 
 
 
 3 
 
 
 
 
 T 
 
 
 P 
 
 
 + 
 
 
 F 
 
 
 P 
 
 
 + 
 
 
 F 
 
 
 N 
 
 
 = 
 
 
 5 
 
 
 
 
 = 
 
 
 60 
 
 
 % 
 
 
 
 IoU=\frac{交集=3}{并集=5} = \frac{TP=3}{TP+FP+FN=5} = 60\% 
 
 
 IoU=并集=5交集=3​=TP+FP+FN=5TP=3​=60%


### 2.2. 代码中如何表达

IOU evaluation

def binary_iou(s, g):
assert (len(s.shape) == len(g.shape))
# 两者相乘值为1的部分为交集
intersecion = np.multiply(s, g)
# 两者相加，值大于0的部分为交集
union = np.asarray(s + g > 0, np.float32)
iou = intersecion.sum() / (union.sum() + 1e-10)
return iou
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0