LeetCode 刷题基础 -- 模板原型Ⅱ_晴问算法训练营-优快云博客

模板原型 - 提高篇

学习网站

学习网站

一、二叉树

① 先序遍历

struct Node {
    int l, r;
} nodes[MAXN];

vector<int> pre;

void preOrder(int root) {
    if (root == -1) {
        return;
    }
    pre.push_back(root);
    preOrder(nodes[root].l);
    preOrder(nodes[root].r);
}

② 层序遍历

void layerOrder(int root) {
    queue<int> q;
    q.push(root);
    while (!q.empty()) {
        int front = q.front();
        q.pop();
        layer.push_back(front);
        if (nodes[front].l != -1) {
            q.push(nodes[front].l);
        }
        if (nodes[front].r != -1) {
            q.push(nodes[front].r);
        }
    }
}

③ 二叉树的高度

int getHeight(int root) {
    if (root == -1) {
        return 0;
    }
    int leftHeight = getHeight(nodes[root].l);
    int rightHeight = getHeight(nodes[root].r);
    return max(leftHeight, rightHeight) + 1;
}

④ 翻转二叉树

void revert(int root) {
    if (root == -1) {
        return;
    }
    revert(nodes[root].l);
    revert(nodes[root].r);
    swap(nodes[root].l, nodes[root].r);
}

⑤ 先序中序还原二叉树

vector<int> pre, in, post;

int buildTree(int preL, int preR, int inL, int inR) {
    if (preL > preR) {
        return -1;
    }
    int root = pre[preL];
    int inIndexOfRoot;
    for (int i = inL; i <= inR; i++) {
        if (in[i] == root) {
            inIndexOfRoot = i;
            break;
        }
    }
    int leftCount = inIndexOfRoot - inL;
    nodes[root].l = buildTree(preL + 1, preL + leftCount, inL, inIndexOfRoot - 1);
    nodes[root].r = buildTree(preL + leftCount + 1, preR, inIndexOfRoot + 1, inR);
    return root;
}

⑥ 二叉树的最近公共祖先

现有一棵n个结点的二叉树（结点编号为从0到n-1，根结点为0号结点），求两个指定编号结点的最近公共祖先。

注：二叉树上两个结点A、B的最近公共祖先是指：二叉树上存在的一个结点P，使得P既是A的祖先，又是B的祖先，并且P需要离根结点尽可能远（即层号尽可能大）。

int LCA(int root, int p, int q) {
    if (root == -1) {
        return -1;
    }
    if (root == p || root == q) {
        return root;
    }
    int leftResult = LCA(nodes[root].l, p, q);
    int rightResult = LCA(nodes[root].r, p, q);
    if (leftResult != -1 && rightResult != -1) {
        return root;
    } else if (leftResult != -1) {
        return leftResult;
    } else {
        return rightResult;
    }
}

⑦ 二叉树的路径和

int treePathSum = 0;

void getTreePathSum(int root, int nodePathSum) {
    if (root == -1) {
        return;
    }
    nodePathSum += nodes[root].data;
    if (nodes[root].l == -1 && nodes[root].r == -1) {
        treePathSum += nodePathSum;
    } else {
        getTreePathSum(nodes[root].l, nodePathSum);
        getTreePathSum(nodes[root].r, nodePathSum);
    }
}

二、树

① 先序遍历

struct Node {
    vector<int> children;
} nodes[MAXN];

vector<int> pre;

void preOrder(int root) {
    pre.push_back(root);
    for (int i = 0; i < nodes[root].children.size(); i++) {
        preOrder(nodes[root].children[i]);
    }
}

② 层序遍历

struct Node {
    vector<int> children;
} nodes[MAXN];

void layerOrder(int root) {
    queue<int> q;
    q.push(root);
    while (!q.empty()) {
        int front = q.front();
        q.pop();
        layer.push_back(front);
        for (int i = 0; i < nodes[front].children.size(); i++) {
            q.push(nodes[front].children[i]);
        }
    }
}

③ 树的高度

int getHeight(int root) {
    int maxHeight = 0;
    for (int i = 0; i < nodes[root].children.size(); i++) {
        maxHeight = max(maxHeight, getHeight(nodes[root].children[i]));
    }
    return maxHeight + 1;
}

④ 树的结点层号

int layers[MAXN];

void layerOrder(int root) {
    queue<int> q;
    q.push(root);
    int layer = 1;
    while (!q.empty()) {
        int cnt = q.size();
        for (int i = 0; i < cnt; i++) {
            int front = q.front();
            q.pop();
            layers[front] = layer;
            for (int i = 0; i < nodes[front].children.size(); i++) {
                q.push(nodes[front].children[i]);
            }
        }
        layer++;
    }
}

⑤ 树的路径之和

int treePathSum = 0;

void getTreePathSum(int root, int nodePathSum) {
    nodePathSum += nodes[root].data;
    if (nodes[root].children.empty()) {
        treePathSum += nodePathSum;
    }
    for (int i = 0; i < nodes[root].children.size(); i++) {
        getTreePathSum(nodes[root].children[i], nodePathSum);
    }
}

三、二叉查找树

① 二叉查找树的建立

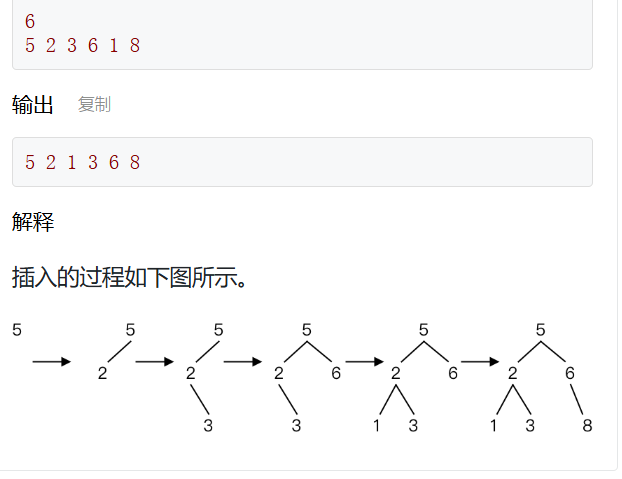
typedef struct node {
	int data;
	struct node *left;
	struct node *right;
}Node;

typedef struct tree {
	Node *root;
}Tree;

void create_tree(Tree *tree, int val)
{
	Node *node = (Node*)malloc(sizeof(Node));  //定于一个节点，将数放到节点中
	node->data = val;
	node->left = NULL;
	node->right = NULL;
	
	if (tree->root == NULL) {
		tree->root = node;   //如果根为空，就将这个节点放到根节点
	}
	else {
		Node *temp = tree->root;  //定义指针指向根节点
		while (temp != NULL) {
			if (val < temp->data) {  //如果要放入的值小于根节点
				if (temp->left == NULL) {  //根节点左孩为空，就直接放入
					temp->left = node;
					return;
				}
				else {
					temp = temp->left;  //根节点左孩不为空，就指向下一个左孩节点
				}
			}
			else {
				if (temp->right == NULL) { //右孩为空，直接放入
					temp->right = node;
					return;
				}
				else {
					temp = temp->right;  //右孩不为空，指向下一个右孩节点
				}
			}
		}
	}
}
int main(int argc, char **argv)
{
	int a[7] = {7,4,5,6,1,8,9};
	Tree tree;
	tree.root = NULL;
	int i;
	int len = sizeof(a) / sizeof(int);
	for (i=0; i<len; i++) {
		create_tree(&tree, a[i]);
	}
	return 0;
}

② 二叉排序树的判定

bool isBSTUtil(TreeNode* node, int min, int max) {
    if (node == NULL) return true;
    if (node->val < min || node->val > max) return false;
    return isBSTUtil(node->left, min, node->val - 1) && isBSTUtil(node->right, node->val + 1, max);
}

bool isBST(TreeNode* root) {
    return isBSTUtil(root, INT_MIN, INT_MAX);
}

四、并查集

① 学校的班级个数

现有一个学校，学校中有若干个班级，每个班级中有若干个学生，每个学生只会存在于一个班级中。如果学生A和学生B处于一个班级，学生B和学生C处于一个班级，那么我们称学生A和学生C也处于一个班级。

现已知学校中共n个学生（编号为从1到n），并给出m组学生关系（指定两个学生处于一个班级），问总共有多少个班级。

const int MAXN = 100;
int father[MAXN];

int findFather(int x) {
    if(x==father[x]){
        return x;
    }else{
        return findFather(father[x]);
    }
}

void unionSet(int a, int b) {
    int faA = findFather(a);
    int faB = findFather(b);
    if (faA != faB) {
        father[faA] = faB;
    }
}

void init(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
    }
}

int main() {
    int n, m, a, b;
    scanf("%d%d", &n, &m);
    init(n);
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &a, &b);
        unionSet(a - 1, b - 1);
    }
    int classCount = 0;
    for (int i = 0; i < n; i++) {
        if (father[i] == i) {
            classCount++;
        }
    }
    printf("%d", classCount);
    return 0;
}

② 学校的班级人数

现已知学校中共n个学生（编号为从1到n），并给出m组学生关系（指定两个学生处于一个班级），问总共有多少个班级，并按降序给出每个班级的人数。

int main() {
    int n, m, a, b;
    scanf("%d%d", &n, &m);
    init(n);
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &a, &b);
        unionSet(a - 1, b - 1);
    }
    for (int i = 0; i < n; i++) {
        studentCount[findFather(i)]++;
    }
    for (int i = 0; i < n; i++) {
        if (studentCount[i] > 0) {
            classes.push_back(studentCount[i]);
        }
    }
    sort(classes.rbegin(), classes.rend());
    printf("%d\n", (int)classes.size());
    return 0;
}

五、堆

① 数据流第 k 大元素

现有一个初始为空的序列S，对其执行n个操作，每个操作是以下两种操作之一：

往序列S中加入一个正整数x；
输出当前序列S中第k大的数。

其中，第k大是指将序列从大到小排序后的第k个数。

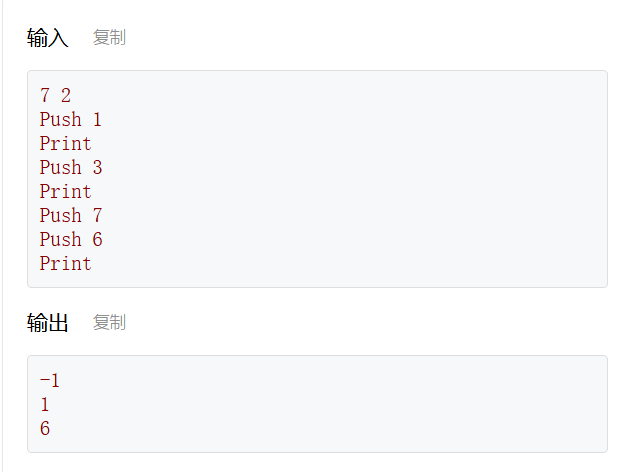
int main() {
    priority_queue<int, vector<int>, greater<int> > q;
    int n, k, x;
    cin >> n >> k;
    string action;
    for (int i = 0; i < n; i++) {
        cin >> action;
        if (action == "Print") {

            if (q.size() >= k) {
                cout << q.top() << endl;
            } else {
                cout << -1 << endl;
            }
        } else if (action == "Push") {
            cin >> x;
            q.push(x);
            if (q.size() > k) {
                q.pop();
            }
        }
    }
    return 0;
}

六、哈夫曼树

① 合并果子

有n堆果子，每堆果子的质量已知，现在需要把这些果子合并成一堆，但是每次只能把两堆果子合并到一起，同时会消耗与两堆果子质量之和等值的体力。显然，在进行n−1次合并之后，就只剩下一堆了。为了尽可能节省体力，需要使耗费的总体力最小。求需要耗费的最小总体力。

int minCostToMergeFruits(vector<int>& fruits) {
    // 使用优先队列（最小堆）来处理
    priority_queue<int, vector<int>, greater<int>> minHeap(fruits.begin(), fruits.end());
    
    int totalCost = 0;
    
    // 当堆中还有超过一个元素时，进行合并操作
    while (minHeap.size() > 1) {
        // 取出最小的两个果堆
        int first = minHeap.top();
        minHeap.pop();
        int second = minHeap.top();
        minHeap.pop();
        
        // 合并这两个果堆
        int mergedCost = first + second;
        totalCost += mergedCost;
        
        // 将新的合并后的果堆放回堆中
        minHeap.push(mergedCost);
    }
    
    return totalCost;
}

七、图的定义和相关术语

① 无向图的度

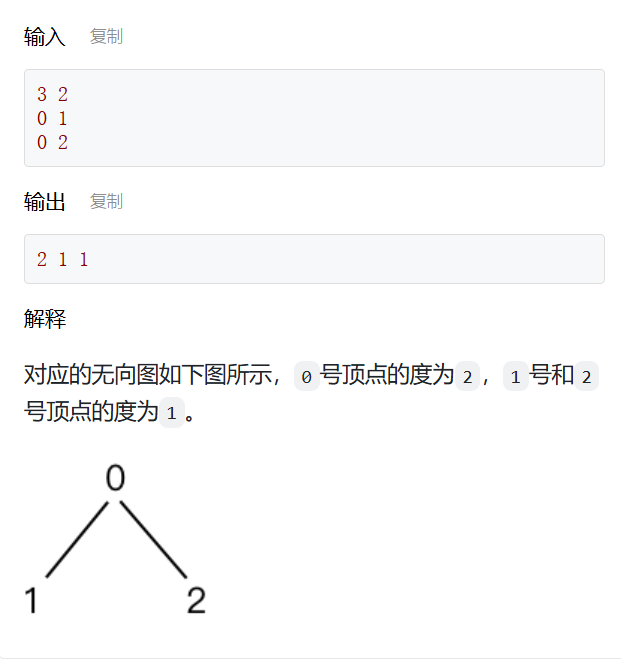
int main() {
    int n, m, u, v;
    scanf("%d%d", &n, &m);
    for (int j = 0; j < m; j++) {
        scanf("%d%d", &u, &v);
        degree[u]++;
        degree[v]++;
    }
    for (int i = 0; i < n; i++) {
        printf("%d", degree[i]);
        if (i < n - 1) {
            printf(" ");
        }
    }
    return 0;
}

② 有向图的度

int main() {
    int n, m, u, v;
    scanf("%d%d", &n, &m);
    for (int j = 0; j < m; j++) {
        scanf("%d%d", &u, &v);
        outDegree[u]++;
        inDegree[v]++;
    }
    for (int i = 0; i < n; i++) {
        printf("%d %d\n", inDegree[i], outDegree[i]);
    }
    return 0;
}

八、图的存储

① 无向图的邻接矩阵

int G[MAXN][MAXN];

int main() {
    memset(G, 0, sizeof(G));
    int n, m, u, v;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u][v] = G[v][u] = 1;
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            printf("%d", G[i][j]);
            printf(j < n - 1 ? " " : "\n");
        }
    }
    return 0;
}

② 无向图的邻接表

const int MAXN = 100;
vector<int> G[MAXN];

int main() {
    int n, m, u, v;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    for (int i = 0; i < n; i++) {
        printf("%d(%d)", i, (int)G[i].size());
        for (int j = 0; j < G[i].size(); j++) {
            printf(" %d", G[i][j]);
        }
        printf("\n");
    }
    return 0;
}

九、图的遍历

① 无向图的连通图

vector<int> G[MAXN];
bool vis[MAXN];

void DFS(int u) {
    vis[u] = true;
    for (int i = 0; i < G[u].size(); i++) {
        int v = G[u][i];
        if (!vis[v]) {
            DFS(v);
        }
    }
}

int main() {
    memset(vis, false, sizeof(vis));
    int n, m, u, v;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    int blockCount = 0;
    for (int i = 0; i < n; i++) {
        if (!vis[i]) {
            DFS(i);
            blockCount++;
        }
    }
    printf("%d", blockCount);
    return 0;
}

② 无向连通图

现有一个共n个顶点、m条边的无向图（假设顶点编号为从0到n-1），判断其是否是连通图。

// 代码是上述代码，若blockCount 为 1，说明为连通图
printf(blockCount == 1 ? "Yes" : "No");

③ 有向图判环

现有一个共n个顶点、m条边的有向图（假设顶点编号为从0到n-1），如果从图中一个顶点出发，沿着图中的有向边前进，最后能回到这个顶点，那么就称其为图中的一个环。判断图中是否有环。

vector<int> G[MAXN];
int vis[MAXN];

bool isCyclic(int u) {
    vis[u] = 0;
    for (int i = 0; i < G[u].size(); i++) {
        int v = G[u][i];
        if (vis[v] == -1 && isCyclic(v)) {
            return true;
        } else if (vis[v] == 0) {
            return true;
        }
    }
    vis[u] = 1;
    return false;
}

int main() {
    memset(vis, -1, sizeof(vis));
    int n, m, u, v;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
    }
    int isCyclicResult = false;
    for (int i = 0; i < n; i++) {
        if (vis[i] == -1 && isCyclic(i)) {
            isCyclicResult = true;
        }
        if (isCyclicResult) {
            break;
        }
    }
    printf(isCyclicResult ? "Yes" : "No");
    return 0;
}

④ 无向图的顶点层号

现有一个共n个顶点、m条边的无向连通图（假设顶点编号为从0到n-1）。我们称从s号顶点出发到达其他顶点经过的最小边数称为各顶点的层号。求图中所有顶点的层号。

#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

const int MAXN = 100;
vector<int> G[MAXN];
bool inQueue[MAXN] = {false};
int layers[MAXN];

void BFS(int s) {
    queue<int> q;
    q.push(s);
    inQueue[s] = true;
    int layer = 0;
    while (!q.empty()) {
        int cnt = q.size();
        for (int i = 0; i < cnt; i++) {
            int front = q.front();
            q.pop();
            layers[front] = layer;
            for (int j = 0; j < G[front].size(); j++) {
                int v = G[front][j];
                if (!inQueue[v]) {
                    q.push(v);
                    inQueue[v] = true;
                }
            }
        }
        layer++;
    }
}

int main() {
    int n, m, start, u, v;
    scanf("%d%d%d", &n, &m, &start);
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    BFS(start);
    for (int i = 0; i < n; i++) {
        printf("%d", layers[i]);
        if (i < n - 1) {
            printf(" ");
        }
    }
    return 0;
}

十、最短路径

① 最短距离

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离。求从s号城市出发到达t号城市的最短距离。

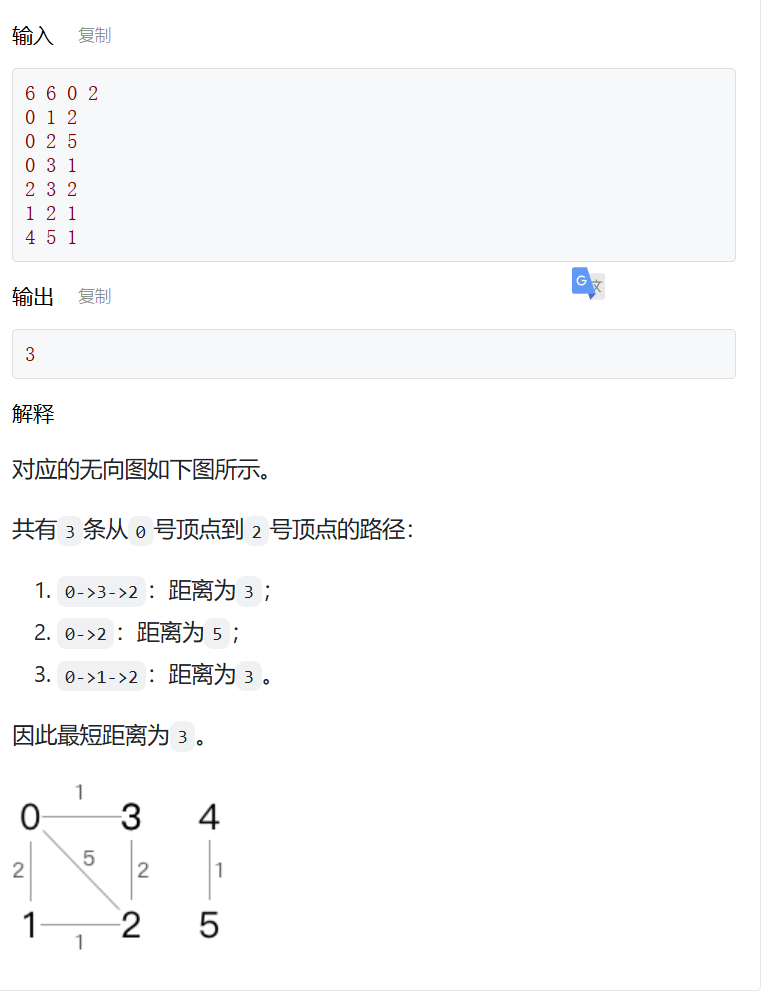
const int MAXN = 100;
const int INF = 1e9;

struct Edge {
    int v, dis;
    Edge(int _v, int _dis) {
        v = _v, dis = _dis;
    }
};

vector<Edge> G[MAXN];
int d[MAXN];
bool vis[MAXN];

void dijkstra(int n, int s) {
    fill(d, d + MAXN, INF);
    memset(vis, false, sizeof(vis));
    d[s] = 0;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return;
        }
        vis[u] = true;
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            if (!vis[v] && d[u] + dis < d[v]) {
                d[v] = d[u] + dis;
            }
        }
    }
}

int main() {
    int n, m, s, t;
    scanf("%d%d%d%d", &n, &m, &s, &t);
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back(Edge(v, w));
        G[v].push_back(Edge(u, w));
    }
    dijkstra(n, s);
    if (d[t] == INF) {
        printf("-1");
    } else {
        printf("%d", d[t]);
    }
    return 0;
}

② 最短距离 - 多终点

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离。求从s号城市出发到达其他每个城市的最短距离。

int main() {
    int n, m, s;
    scanf("%d%d%d", &n, &m, &s);
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back(Edge(v, w));
        G[v].push_back(Edge(u, w));
    }
    dijkstra(n, s);         // 与上题的 dijkstra 一样
    for (int i = 0; i < n; i++) {
        if (d[i] == INF) {
            printf("-1");
        } else {
            printf("%d", d[i]);
        }
        if (i < n - 1) {
            printf(" ");
        }
    }
    return 0;
}

③ 最短距离 - 多边权

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有两种边权，分别代表两个城市之间的距离和花费。求从s号城市出发到达t号城市的最短距离，并在达到最短距离的路径中计算最少花费。

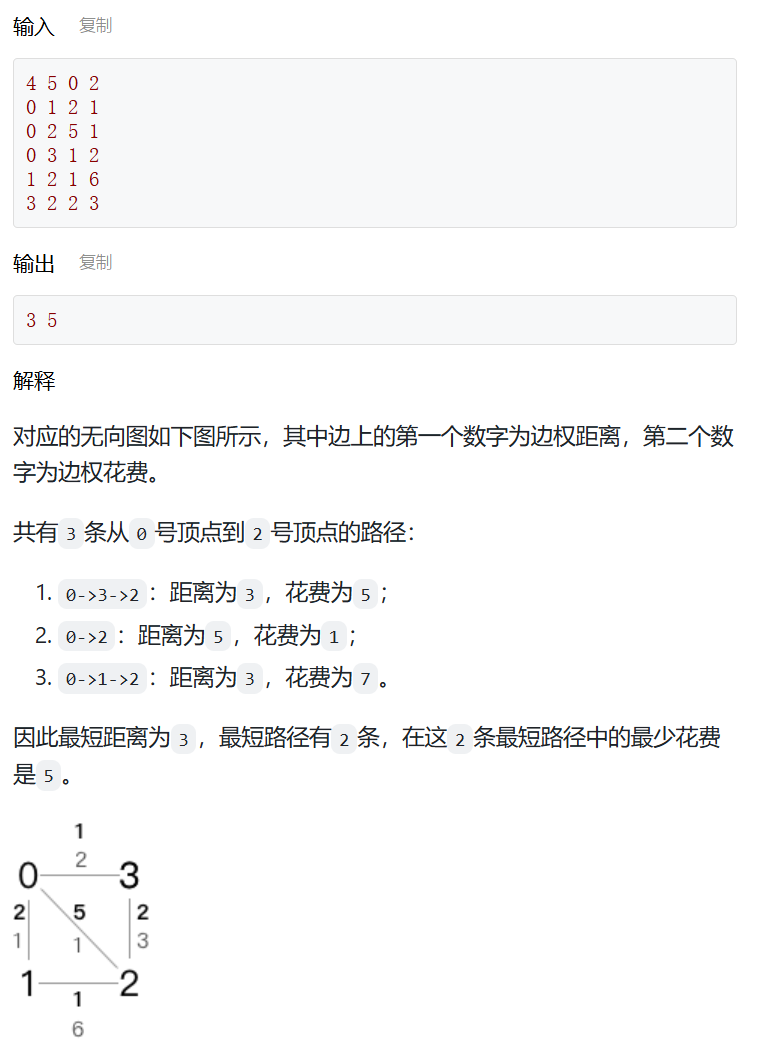
const int MAXN = 100;
const int INF = 1e9;

struct Edge {
    int v, dis, cost;
    Edge(int _v, int _dis, int _cost) {
        v = _v, dis = _dis, cost = _cost;
    }
};

vector<Edge> G[MAXN];
int d[MAXN], c[MAXN];
bool vis[MAXN];

void dijkstra(int n, int s) {
    fill(d, d + MAXN, INF);
    fill(c, c + MAXN, INF);
    memset(vis, false, sizeof(vis));
    d[s] = 0;
    c[s] = 0;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return;
        }
        vis[u] = true;
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            int cost = G[u][j].cost;
            if (!vis[v]) {
                if (d[u] + dis < d[v]) {
                    d[v] = d[u] + dis;
                    c[v] = c[u] + cost;
                } else if (d[u] + dis == d[v] && c[u] + cost < c[v]) {
                    c[v] = c[u] + cost;
                }
            }
        }
    }
}

int main() {
    int n, m, s, t;
    scanf("%d%d%d%d", &n, &m, &s, &t);
    int u, v, dis, cost;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d%d", &u, &v, &dis, &cost);
        G[u].push_back(Edge(v, dis, cost));
        G[v].push_back(Edge(u, dis, cost));
    }
    dijkstra(n, s);
    printf("%d %d", d[t], c[t]);
    return 0;
}

④ 最短路径条数

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离。求从s号城市出发到达t号城市的最短距离和最短路径条数。

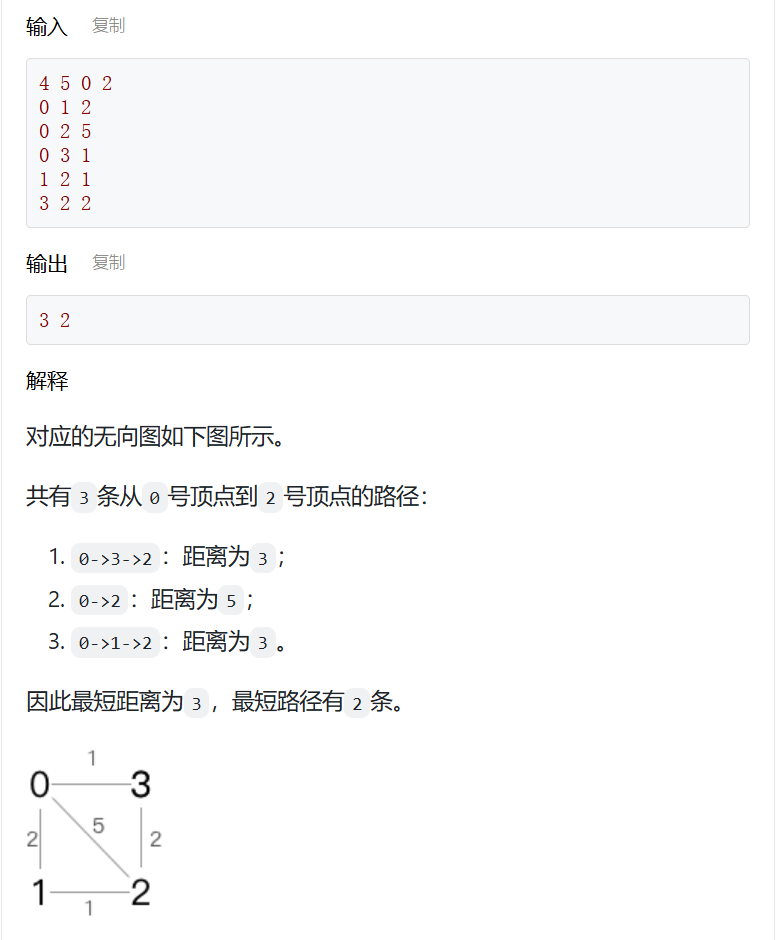
void dijkstra(int n, int s) {
    fill(d, d + MAXN, INF);
    memset(pathCount, 0, sizeof(pathCount));
    memset(vis, false, sizeof(vis));
    d[s] = 0;
    pathCount[s] = 1;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return;
        }
        vis[u] = true;
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            if (!vis[v]) {
                if (d[u] + dis < d[v]) {
                    d[v] = d[u] + dis;
                    pathCount[v] = pathCount[u];
                } else if (d[u] + dis == d[v]) {
                    pathCount[v] += pathCount[u];
                }
            }
        }
    }
}

int main() {
    int n, m, s, t;
    scanf("%d%d%d%d", &n, &m, &s, &t);
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back(Edge(v, w));
        G[v].push_back(Edge(u, w));
    }
    dijkstra(n, s);
    printf("%d %d", d[t], pathCount[t]);
    return 0;
}

⑤ 最短路径

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离。求从s号城市出发到达t号城市的最短距离和最短路径。

vector<Edge> G[MAXN];
int d[MAXN], pre[MAXN];
bool vis[MAXN];

void dijkstra(int n, int s) {
    fill(d, d + MAXN, INF);
    memset(pre, -1, sizeof(pre));
    memset(vis, false, sizeof(vis));
    d[s] = 0;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return;
        }
        vis[u] = true;
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            if (!vis[v] && d[u] + dis < d[v]) {
                d[v] = d[u] + dis;
                pre[v] = u;
            }
        }
    }
}

vector<int> path;

void DFS(int v, int s) {
    if (v == s) {
        path.push_back(v);
        return;
    }
    DFS(pre[v], s);
    path.push_back(v);
}

int main() {
    int n, m, s, t;
    scanf("%d%d%d%d", &n, &m, &s, &t);
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back(Edge(v, w));
        G[v].push_back(Edge(u, w));
    }
    dijkstra(n, s);
    DFS(t, s);
    printf("%d ", d[t]);
    for (int i = 0; i < path.size(); i++) {
        printf("%d", path[i]);
        if (i < (int)path.size() - 1) {
            printf("->");
        }
    }
    return 0;
}

⑥ 最短路径 - 多边权

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有两种边权，分别代表两个城市之间的距离和花费。求从s号城市出发到达t号城市的最短距离，并在达到最短距离的路径中计算最少花费，同时给出相应的最短路径。

// 仅修改 dijkstra
void dijkstra(int n, int s) {
    fill(d, d + MAXN, INF);
    fill(c, c + MAXN, INF);
    memset(pre, -1, sizeof(pre));
    memset(vis, false, sizeof(vis));
    d[s] = 0;
    c[s] = 0;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return;
        }
        vis[u] = true;
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            int cost = G[u][j].cost;
            if (!vis[v]) {
                if (d[u] + dis < d[v]) {
                    d[v] = d[u] + dis;
                    c[v] = c[u] + cost;
                    pre[v] = u;
                } else if (d[u] + dis == d[v] && c[u] + cost < c[v]) {
                    c[v] = c[u] + cost;
                    pre[v] = u;
                }
            }
        }
    }
}

⑦ 最短路径 - 多路径

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离。求从s号城市出发到达t号城市的最短路径条数和最短路径（可能有多条）。

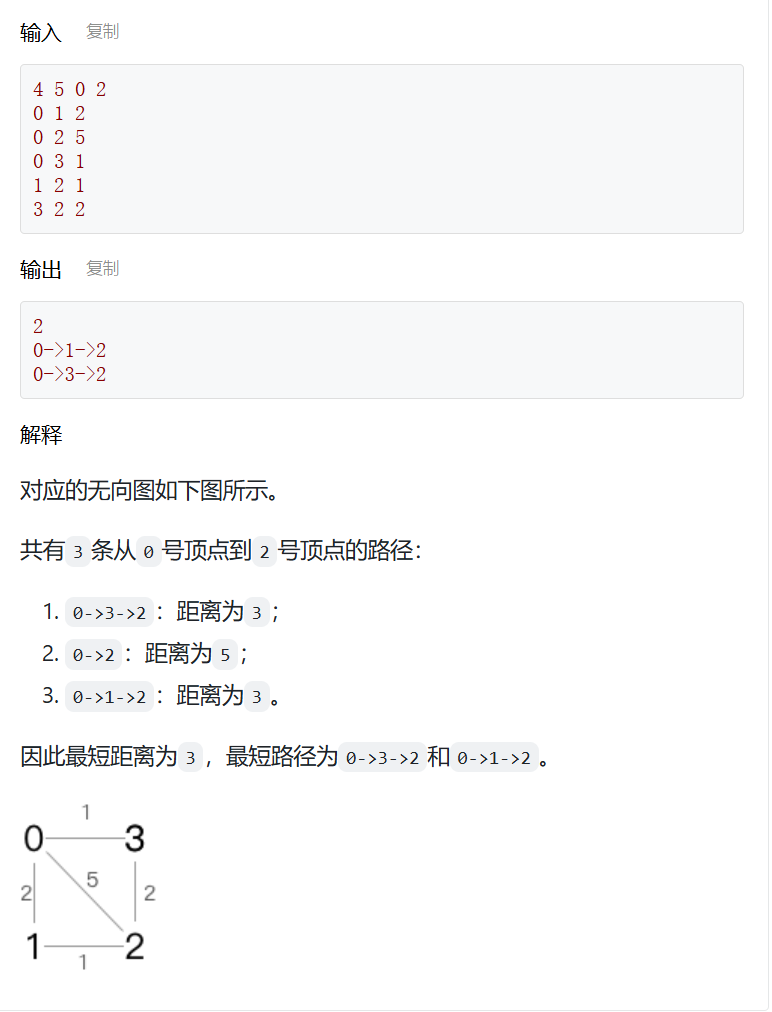
struct Edge {
    int v, dis;
    Edge(int _v, int _dis) {
        v = _v, dis = _dis;
    }
};

vector<Edge> G[MAXN];
int d[MAXN];
bool vis[MAXN];
vector<int> pre[MAXN];

void dijkstra(int n, int s) {
    fill(d, d + MAXN, INF);
    memset(vis, false, sizeof(vis));
    d[s] = 0;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return;
        }
        vis[u] = true;
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            if (!vis[v]) {
                if (d[u] + dis < d[v]) {
                    d[v] = d[u] + dis;
                    pre[v].clear();
                    pre[v].push_back(u);
                } else if (d[u] + dis == d[v]) {
                    pre[v].push_back(u);
                }
            }
        }
    }
}

vector<vector<int> > paths;
vector<int> tempPath;

void DFS(int v, int s) {
    if (v == s) {
        tempPath.push_back(v);
        paths.push_back(tempPath);
        tempPath.pop_back();
        return;
    }
    tempPath.push_back(v);
    for (int i = 0; i < pre[v].size(); i++) {
        DFS(pre[v][i], s);
    }
    tempPath.pop_back();
}

int main() {
    int n, m, s, t;
    scanf("%d%d%d%d", &n, &m, &s, &t);
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back(Edge(v, w));
        G[v].push_back(Edge(u, w));
    }
    dijkstra(n, s);
    DFS(t, s);
    for (int i = 0; i < paths.size(); i++) {
        reverse(paths[i].begin(), paths[i].end());
    }
    sort(paths.begin(), paths.end());
    printf("%d\n", (int)paths.size());
    for (int i = 0; i < paths.size(); i++) {
        for (int j = 0; j < paths[i].size(); j++) {
            printf("%d", paths[i][j]);
            if (j < (int)paths[i].size() - 1) {
                printf("->");
            }
        }
        printf("\n");
    }
    return 0;
}

⑧ 最短距离 - 多起点多终点

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离。求从所有城市出发到达所有城市的所有最短距离。

const int MAXN = 50;
const int INF = 1e9;

int d[MAXN][MAXN];

void floyd(int n) {
    for (int k = 0; k < n; k++) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (d[i][k] != INF && d[k][j] != INF && d[i][k] + d[k][j] < d[i][j]) {
                    d[i][j] = d[i][k] + d[k][j];
                }
            }
        }
    }
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    fill(d[0], d[0] + MAXN * MAXN, INF);
    for (int i = 0; i < n; i++) {
        d[i][i] = 0;
    }
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        d[u][v] = d[v][u] = w;
    }
    floyd(n);
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (d[i][j] == INF) {
                printf("-1");
            } else {
                printf("%d", d[i][j]);
            }
            if (j < n - 1) {
                printf(" ");
            }
        }
        printf("\n");
    }
    return 0;
}

⑨ 最短路径 - 多边权Ⅱ

现有一个共n个顶点（代表城市）、m条边（代表道路）的无向图（假设顶点编号为从0到n-1），每条边有各自的边权，代表两个城市之间的距离；每个顶点有各自的点权，代表城市的堵车指数。求从s号城市出发到达t号城市的最短距离与最短路径。

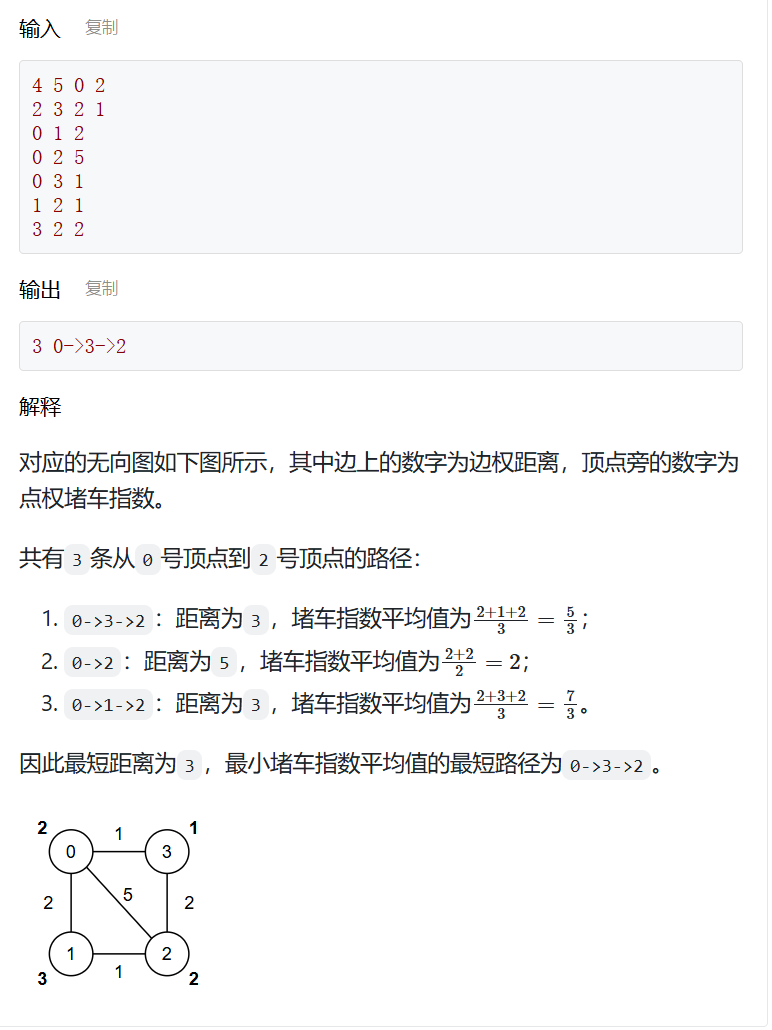
vector<Edge> G[MAXN];
int weight[MAXN], d[MAXN];
bool vis[MAXN];
vector<int> pre[MAXN];

void dijkstra(int n, int s) {
    fill(d, d + MAXN, INF);
    memset(vis, false, sizeof(vis));
    d[s] = 0;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return;
        }
        vis[u] = true;
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            if (!vis[v]) {
                if (d[u] + dis < d[v]) {
                    d[v] = d[u] + dis;
                    pre[v].clear();
                    pre[v].push_back(u);
                } else if (d[u] + dis == d[v]) {
                    pre[v].push_back(u);
                }
            }
        }
    }
}

vector<int> tempPath, optPath;
double optValue = INF;

void DFS(int v, int s) {
    if (v == s) {
        tempPath.push_back(v);
        int weightSum = 0;
        for (int i = 0; i < tempPath.size(); i++) {
            weightSum += weight[tempPath[i]];
        }
        double weightAvg = (double)weightSum / tempPath.size();
        if (weightAvg < optValue) {
            optValue = weightAvg;
            optPath = tempPath;
        }
        tempPath.pop_back();
        return;
    }
    tempPath.push_back(v);
    for (int i = 0; i < pre[v].size(); i++) {
        DFS(pre[v][i], s);
    }
    tempPath.pop_back();
}

int main() {
    int n, m, s, t;
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for (int i = 0; i < n; i++) {
        scanf("%d", &weight[i]);
    }
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back(Edge(v, w));
        G[v].push_back(Edge(u, w));
    }
    dijkstra(n, s);
    DFS(t, s);
    printf("%d ", d[t]);
    reverse(optPath.begin(), optPath.end());
    for (int i = 0; i < optPath.size(); i++) {
        printf("%d", optPath[i]);
        if (i < (int)optPath.size() - 1) {
            printf("->");
        }
    }
    return 0;
}

十一、最小生成树

① 最小生成树-Prim算法

现有一个共n个顶点、m条边的无向图（假设顶点编号为从0到n-1），每条边有各自的边权。在图中寻找一棵树，使得这棵树包含图上所有顶点、所有边都是图上的边，且树上所有边的边权之和最小。使用Prim算法求出这个边权之和的最小值。

struct Edge {
    int v, dis;
    Edge(int _v, int _dis) {
        v = _v, dis = _dis;
    }
};

vector<Edge> G[MAXN];
int d[MAXN];
bool vis[MAXN];

int prim(int n) {
    fill(d, d + MAXN, INF);
    memset(vis, false, sizeof(vis));
    d[0] = 0;
    int weightSum = 0;
    for (int i = 0; i < n; i++) {
        int u = -1, minDis = INF;
        for (int j = 0; j < n; j++) {
            if (!vis[j] && d[j] < minDis) {
                u = j;
                minDis = d[j];
            }
        }
        if (u == -1) {
            return -1;
        }
        vis[u] = true;
        weightSum += d[u];
        for (int j = 0; j < G[u].size(); j++) {
            int v = G[u][j].v;
            int dis = G[u][j].dis;
            if (!vis[v] && dis < d[v]) {
                d[v] = dis;
            }
        }
    }
    return weightSum;
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        G[u].push_back(Edge(v, w));
        G[v].push_back(Edge(u, w));
    }
    int weightSum = prim(n);
    printf("%d", weightSum);
    return 0;
}

② 最小生成树-Kruskal算法

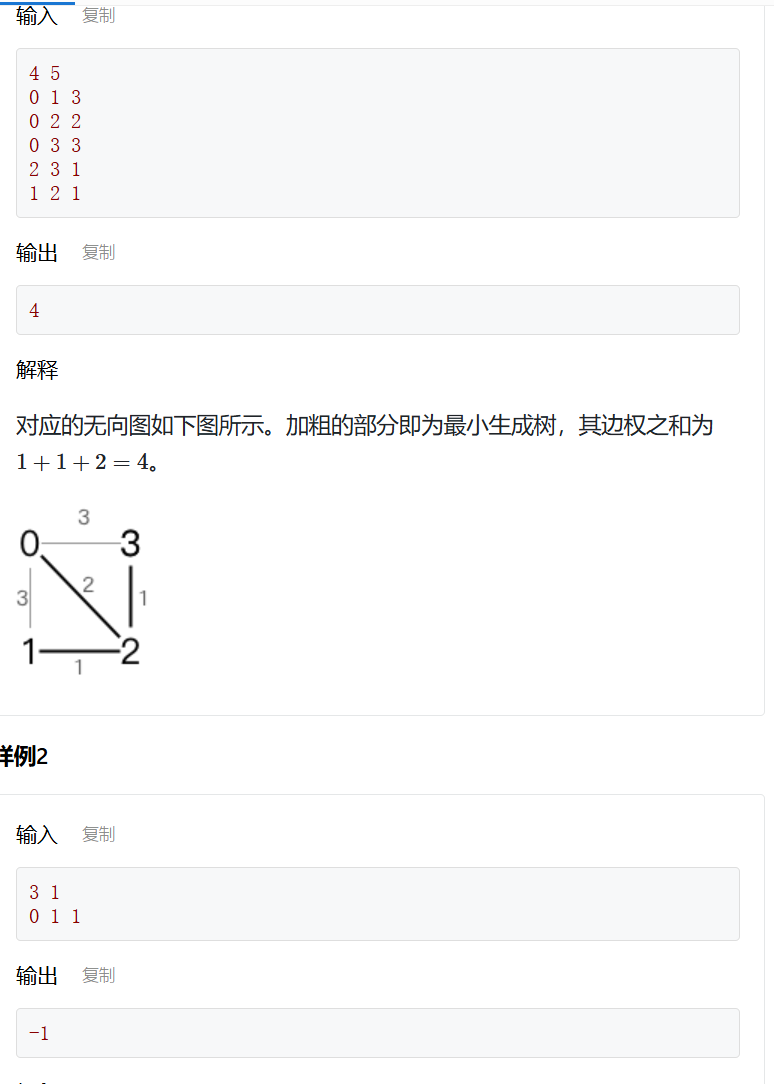
struct Edge {
    int u, v, w;
    Edge(int _u, int _v, int _w) {
        u = _u, v = _v, w = _w;
    }
};

vector<Edge> edges;

bool cmp(Edge a, Edge b) {
    return a.w < b.w;
}

int father[MAXN];

int findFather(int x) {
    int xCopy = x;
    while (father[x] != x) {
        x = father[x];
    }
    int root = x;
    x = xCopy;
    while (father[x] != x) {
        int fatherX = father[x];
        father[x] = root;
        x = fatherX;
    }
    return root;
}

int kruskal(int n, int m) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
    }
    int weightSum = 0, edgeCount = 0;
    sort(edges.begin(), edges.end(), cmp);
    for (int i = 0; i < m; i++) {
        int faU = findFather(edges[i].u);
        int faV = findFather(edges[i].v);
        if (faU != faV) {
            father[faU] = faV;
            weightSum += edges[i].w;
            edgeCount++;
        }
        if (edgeCount == n - 1) {
            break;
        }
    }
    if (edgeCount != n - 1) {
        return -1;
    } else {
        return weightSum;
    }
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    int u, v, w;
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &w);
        edges.push_back(Edge(u, v, w));
    }
    int weightSum = kruskal(n, m);
    printf("%d", weightSum);
    return 0;
}

十二、拓扑排序

① 拓扑排序

现有一个共n个顶点、m条边的有向无环图（假设顶点编号为从0到n-1）。输出该图的拓扑排序序列。

注：每次有多个顶点可以选择时，总是选择编号最小的那个。

const int MAXN = 100;

vector<int> G[MAXN];
int inDegree[MAXN];
vector<int> topoOrder;

void topoSort(int n) {
    priority_queue<int, vector<int>, greater<int> > q;
    for (int i = 0; i < n; i++) {
        if (inDegree[i] == 0) {
            q.push(i);
        }
    }
    while (!q.empty()) {
        int u = q.top();
        q.pop();
        topoOrder.push_back(u);
        for (int i = 0; i < G[u].size(); i++) {
            int v = G[u][i];
            inDegree[v]--;
            if (inDegree[v] == 0) {
                q.push(v);
            }
        }
        G[u].clear();
    }
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    int u, v;
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        inDegree[v]++;
    }
    topoSort(n);
    for (int i = 0; i < topoOrder.size(); i++) {
        printf("%d", topoOrder[i]);
        if (i < (int)topoOrder.size() - 1) {
            printf(" ");
        }
    }
    return 0;
}

② 有向无环图的判定-拓扑排序

现有一个共n个顶点、m条边的有向图（假设顶点编号为从0到n-1）。使用拓扑排序判断其是否是有向无环图，即该有向图中是否有环。

const int MAXN = 100;

vector<int> G[MAXN];
int inDegree[MAXN];

bool topoSort(int n) {
    int vertexCount = 0;
    priority_queue<int, vector<int>, greater<int> > q;
    for (int i = 0; i < n; i++) {
        if (inDegree[i] == 0) {
            q.push(i);
        }
    }
    while (!q.empty()) {
        int u = q.top();
        q.pop();
        for (int i = 0; i < G[u].size(); i++) {
            int v = G[u][i];
            inDegree[v]--;
            if (inDegree[v] == 0) {
                q.push(v);
            }
        }
        G[u].clear();
        vertexCount++;
    }
    return vertexCount == n;
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    int u, v;
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        inDegree[v]++;
    }
    printf(topoSort(n) ? "Yes" : "No");
    return 0;
}

③ 先导课程

现有n门课程（假设课程编号为从0到n-1），课程之间有依赖关系，即可能存在两门课程，必须学完其中一门才能学另一门。现在给出m个依赖关系，问能否把所有课程都学完。

注：能同时学习多门课程时总是先学习编号最小的课程。

const int MAXN = 100;

vector<int> G[MAXN];
int inDegree[MAXN];
vector<int> topoOrder;

int topoSort(int n) {
    int vertexCount = 0;
    priority_queue<int, vector<int>, greater<int> > q;
    for (int i = 0; i < n; i++) {
        if (inDegree[i] == 0) {
            q.push(i);
        }
    }
    while (!q.empty()) {
        int u = q.top();
        q.pop();
        topoOrder.push_back(u);
        for (int i = 0; i < G[u].size(); i++) {
            int v = G[u][i];
            inDegree[v]--;
            if (inDegree[v] == 0) {
                q.push(v);
            }
        }
        G[u].clear();
        vertexCount++;
    }
    return vertexCount;
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    int u, v;
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        inDegree[v]++;
    }
    int learnCount = topoSort(n);
    if (learnCount == n) {
        printf("Yes\n");
        for (int i = 0; i < topoOrder.size(); i++) {
            printf("%d", topoOrder[i]);
            if (i < (int)topoOrder.size() - 1) {
                printf(" ");
            }
        }
    } else {
        printf("No\n%d\n", n - learnCount);
    }
    return 0;
}