LeetCode 100题 （10题）

1:22. 括号生成

题意：数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

思路：暴搜就好，唯一需要想的是怎么判断括号是否合法，用一个变量var记录就好，如果是 '(' 就让var 加1，如果是')' 就让var减1，如果 var 小于 0 就说明不合法

class Solution {

    public List<String> ans = new ArrayList<>();

    public List<String> generateParenthesis(int n) {
        dfs(0, 0, "", n);
        return ans;
    }

    public void dfs(int cnt1, int cnt2, String s, int sum){
        if(cnt1 > sum || cnt2 > sum) return;
        if(cnt1 == sum && cnt2 == sum){
            int val = 0;
            for(int i = 0; i < s.length(); i ++){
                if(s.charAt(i) == '(') val ++;
                else val --;
                if(val < 0) return;
            }
            if(val == 0) ans.add(s); 
        }
        dfs(cnt1 + 1, cnt2, s + "(", sum);
        dfs(cnt1, cnt2 + 1, s + ")", sum);
    }
}

2：49. 字母异位词分组

题意：给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

思路：如果两个字符串是异位词的话，那么这两个字符串排序后一定是一样的，那就让每个字符串排序后的值作为 key，其本身作为 value，存入一个map中即可

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> map = new HashMap<>();
        for(String str : strs){
            char[] c = str.toCharArray();
            Arrays.sort(c);
            String key = new String(c) ;
            List<String> list = map.getOrDefault(key, new ArrayList<>());
            list.add(str);
            map.put(key, list);
        }
        return new ArrayList<List<String>>(map.values());
    }
}

3：48. 旋转图像

题意：给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

思路：推公式，我们首先观察图像可以发现 matrix[row][col] 经过顺时针90度旋转后会到 martix[col][n - row - 1]这个位置，

也就是得到一个等式：matrix[col][n − row − 1] = matrix[row][col]，

那么这个matrix[col][n − row − 1]会转移到哪呢？

我们此时可以令 row = col, col = n - row - 1, 代入标红的那个等式可以得到：

matrix[n - row - 1][n - col - 1] = matrix[col][n - row - 1]；

那么这个matrix[n - row - 1][n - col - 1]会转移到哪呢？

我们就和上面一样，令 row = n - row - 1, col = n - col - 1，可以得到

matrix[n − col − 1][row] = matrix[n − row − 1][n − col − 1]；

那么这个matrix[n − col − 1][row]会转移到哪呢？

继续令row = n - col - 1, col  = row,即可得到：

matrix[row][col] = matrix[n − col − 1][row]；

可以发现回到了原点，此时我们就发现了规律：

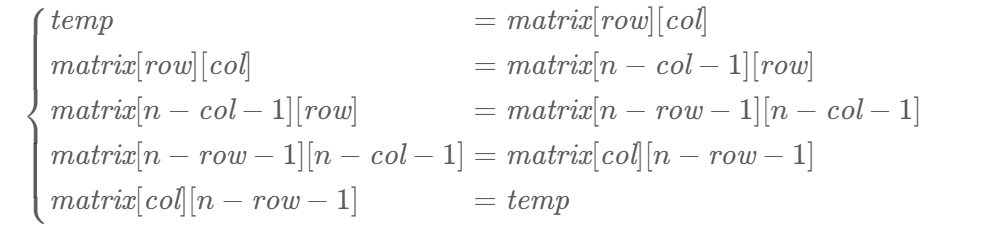
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for(int i = 0; i < (n + 1) / 2; i ++){
            for(int j = 0; j < n / 2; j ++){
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = tmp;
            }
        }
    }
}

4：46. 全排列

题意：给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

思路：dfs的板子题

class Solution {

    List<List<Integer>> ans = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        int n = nums.length;
        boolean[] p = new boolean[n];
        int[] tmp = new int[n];
        dfs(0, nums, p, tmp, n);
        return ans;
    }

    public void dfs(int pos, int[] nums, boolean[] p, int[] tmp, int n){
        if(pos == n){
            List<Integer> tmp1 = new ArrayList<>();
            for(int num : tmp){
                tmp1.add(num);
            }
            ans.add(tmp1);
            return;
        }

        for(int i = 0; i < n; i ++){
            if(p[i]) continue;
            p[i] = true;
            tmp[pos] = nums[i];
            dfs(pos + 1, nums, p, tmp, n);
            p[i] = false;
        }
    }
}

5：42. 接雨水

题意：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

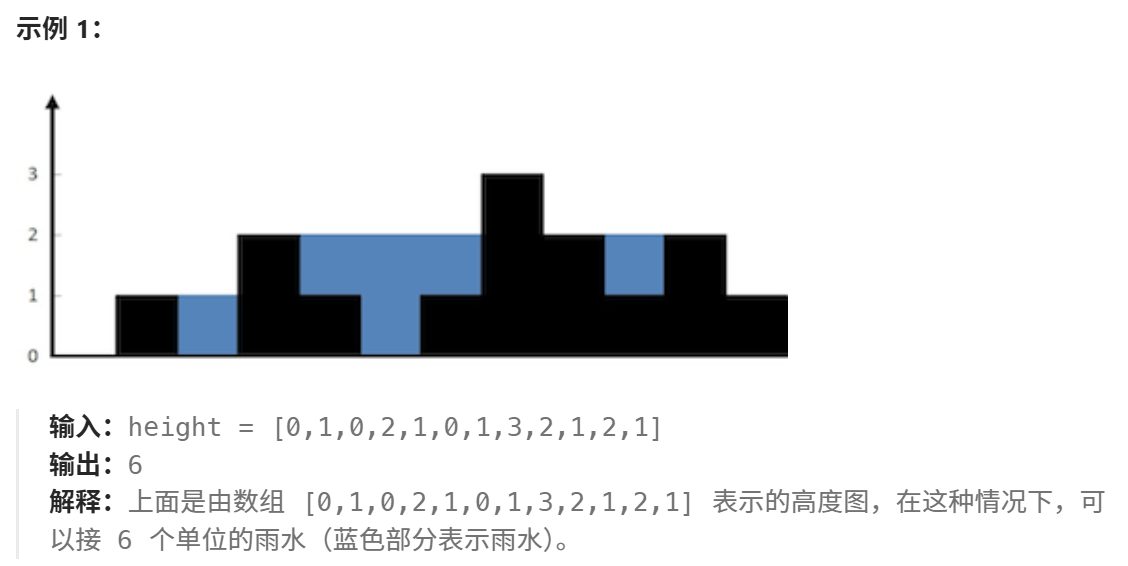
思路：个人感觉是前几十道题里面思维含量最高的一题，这题的难点就是思考什么时候会积累雨水，也就是对答案做出贡献，我们来看这张图，圈出来的地方

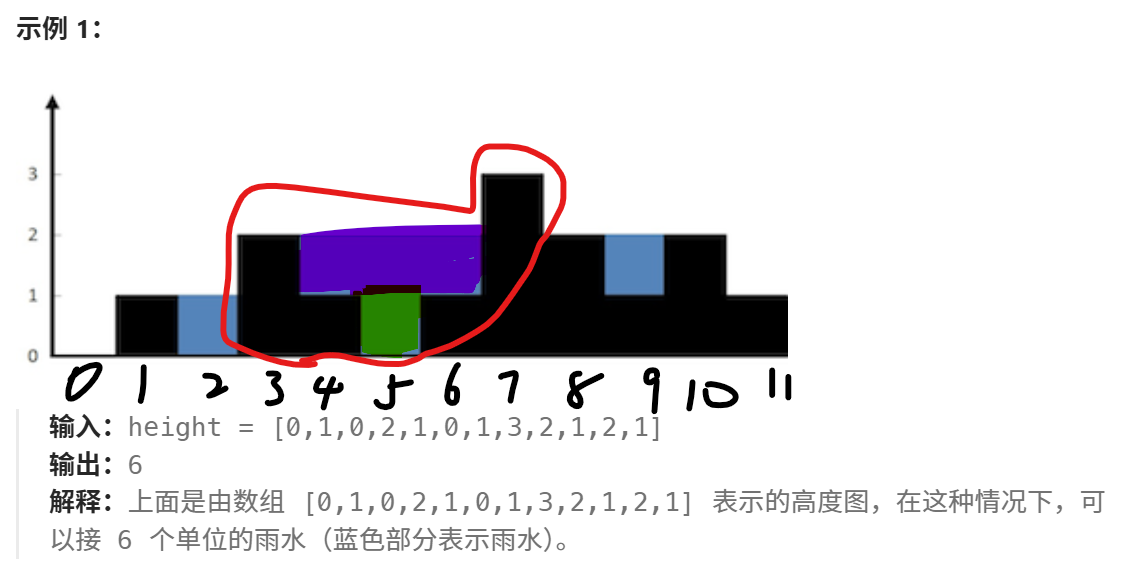
很明显那个绿色的方块是[4，6] 这个区间的三个方块一起贡献的，也就是说当方块h[i]碰到比它大的h[i + 1]，即h[i + 1] > h[i]时，并且还要保证h[i]的左边有比它高的方块，才有可能对答案产生贡献，而紫色的那三个方块是[3，7]这个区间贡献的，因为h[6] < h[7]，并且h[3] > h[6]，这个时侯我就需要知道h[3]的索引用于计算这个紫色方块的宽，而这个紫色方块的高就是h[3] - h[6]了，当然仅限于这张图，因为在别的数据中我们不知道h[3]和h[7]到底哪个大，所以取二者的min用来和宽相乘，即得其对答案做的的贡献。

我们可以用栈来存储每个方块的索引，保证从栈顶到栈尾其索引所对应的方块是降序排列的，这样当我们的栈头方块小于我当前遍历到的 h[i] 时，直接弹出栈头，这时候的栈头一定比刚才弹出去的栈头大，但不确定它和h[i]谁大，所以我们就取二者中的最小值，然后乘以宽即可；

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int ans = 0;
        Stack<Integer> stack = new Stack<>();
        for(int i = 0; i < n; i ++){
            while(!stack.isEmpty() && height[stack.peek()] < height[i]){
                int top = stack.pop();
                if(stack.isEmpty()) break;
                int left = stack.peek();
                int wide = i - left - 1;
                int h = Math.min(height[left], height[i]) - height[top];
                ans += h * wide;
            }
            stack.push(i);
        }
        return ans;
    }
}

6:39. 组合总和

题意：给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的

思路：暴力搜索即可，找出所有的可能性

class Solution {

    List<List<Integer>> ans = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<Integer> tmp = new ArrayList<>();
        dfs(candidates, target, tmp, 0);
        return ans;
    }

    public void dfs(int[] candidates, int target, List<Integer> tmp, int idx){
        if(idx == candidates.length) return;
        if(target == 0){
            ans.add(new ArrayList<>(tmp));
            return;
        }
        // 不选下标为 idx 的数
        dfs(candidates, target, tmp, idx + 1);

        // 选下标为 idx 的数
        if(target - candidates[idx] >= 0){
            tmp.add(candidates[idx]);
            dfs(candidates, target - candidates[idx], tmp, idx);
            tmp.remove(tmp.size() - 1);
        }
    }
}

7：543. 二叉树的直径

题意：给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

思路：每一个节点都可以看成是某个路径的节点，所以直接遍历整个二叉树，以每个节点作为起点时，计算它所能构成的路径的最大长度，也就是以它左子节点为根的子树的最大深度加上以它右子节点为根的子树的最大深度。

不过这个写法的时间复杂度是N^2级别的，我们可以用记忆化将其优化到 0(n)级别

// class Solution {

//     int ans = 0;

//     public int diameterOfBinaryTree(TreeNode root) {
//         dfs2(root);
//         return ans;
//     }

//     public void dfs2(TreeNode node){
//         if(node == null) return;
//         int l_len = 0;
//         int r_len = 0;
//         if(node.left != null) l_len = dfs1(node.left, 1);
//         if(node.right != null) r_len = dfs1(node.right, 1);
//         ans = Math.max(ans, l_len + r_len);
//         dfs2(node.left);
//         dfs2(node.right);
//     }

//     public int dfs1(TreeNode node, int deep){
//         int tmp = deep;
//         if(node.left != null) deep = Math.max(deep, dfs1(node.left, deep + 1));
//         if(node.right != null) deep = Math.max(deep, dfs1(node.right, tmp + 1));
//         return deep;
//     }
// }

class Solution {
    int ans = 0;
    Map<TreeNode, Integer> depthMap = new HashMap<>(); 

    public int diameterOfBinaryTree(TreeNode root) {
        dfs2(root);
        return ans;
    }

    public void dfs2(TreeNode node){
        if(node == null) return;
        
        // 先计算左右子树的深度
        int l_len = dfs1(node.left);
        int r_len = dfs1(node.right);
        
        ans = Math.max(ans, l_len + r_len);
        
        dfs2(node.left);
        dfs2(node.right);
    }

    public int dfs1(TreeNode node) {
        if (node == null) return 0;
        
        // 如果已经计算过，直接返回
        if (depthMap.containsKey(node)) {
            return depthMap.get(node);
        }
        
        // 递归计算深度
        int leftDepth = dfs1(node.left);
        int rightDepth = dfs1(node.right);
        
        // 当前节点的深度 = 左右子树深度的最大值 + 1
        int depth = Math.max(leftDepth, rightDepth) + 1;
        depthMap.put(node, depth);
        
        return depth;
    }
}

8：34. 在排序数组中查找元素的第一个和最后一个位置

题意：给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

思路：二分的模板题，两种写法，分别代表了求出给定目标的开始位置和结束位置

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] ans = new int[2];
        int n = nums.length;

        if(n == 0){
            ans[0] = -1;
            ans[1] = -1;
            return ans;
        }

        int l = 0, r = n - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }

        if(nums[l] != target){
            ans[0] = -1; ans[1] = -1;
            return ans;
        }

        ans[0] = l;

        l = 0; r = n - 1;
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(nums[mid] <= target) l = mid;
            else r = mid - 1;
        }

        ans[1] = l;

        return ans;
    }
}

9：33. 搜索旋转排序数组

题意：整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 向左旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 下标 3 上向左旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

思路：也是一道二分，先用二分判断这个当前区间内的元素是否升序，进一步锁定这个tar的范围，然后再在这个区间内二分找出tar，不过因为二分的边界性，之前我的模板的写法很难调，就直接照着题解写了

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if(n == 0) return -1;
        if(n == 1) return nums[0] == target ? 0 : -1;

        int l = 0; int r = n - 1;
        while(l <= r){
            int mid = l + r >> 1;
            if(nums[mid] == target) return mid;
            if(nums[0] <= nums[mid]){ //[0, mid]是升序
                if(nums[0] <= target && target < nums[mid]){
                    r = mid - 1;
                }else{
                    l = mid + 1;
                }
            }else{  //[mid, n]是升序
                if(nums[mid] < target && target <= nums[n - 1]){
                    l = mid + 1;
                }else{
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
}

10：32. 最长有效括号

题意：给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号 子串 的长度。

左右括号匹配，即每个左括号都有对应的右括号将其闭合的字符串是格式正确的，比如                 "((()))"。

思路：之前碰到过这一类括号匹配的问题，基本上考点都绕不开“栈”这个数据结构，这题也可以用“栈”来解决，栈头只存最新的一个未匹配的右括号的下标，之后存的是左括号的下标，当我们碰见右括号时，就与栈中的左括号进行匹配，也就是弹出栈尾；

那我们的这个栈顶存的东西有什么用呢？这个栈顶存的是最新的未被匹配的 “)” 的索引，我们答案的每次更新一定是在碰到 “)” 的时候， 那么如果之前栈里的“(”已经匹配完了，那么这个时候的答案就是 新遇见的 ")" 的索引减去这个栈顶存的索引，也就是说我们维护了这一段括号的有效长度;

那么当栈为空时，说明此时这个“)”不匹配了，也就是相当于一个断点，把前面匹配的一段给分开了，此时我们把这个“)”的索引存入栈头即可。

class Solution {
    public int longestValidParentheses(String s) {
        Stack<Integer> stack = new Stack<>();
        int n = s.length();
        int ans = 0;

        stack.push(-1);

        for(int i = 0; i < n; i ++){
            if(s.charAt(i) == '('){
                stack.push(i);
            }else{
                stack.pop();
                if(stack.isEmpty()) stack.push(i);
                else ans = Math.max(ans, i - stack.peek());
            }
        }
        return ans;
    }
}