目录
1 快速排序的基本原理
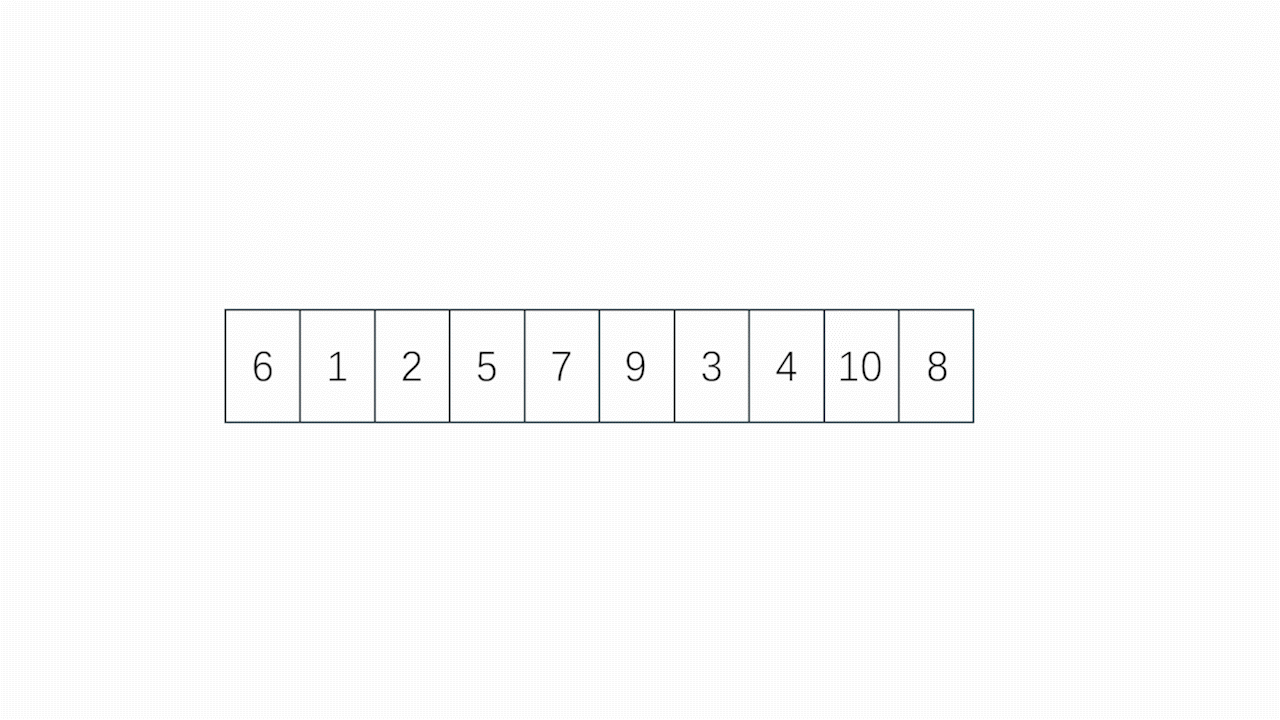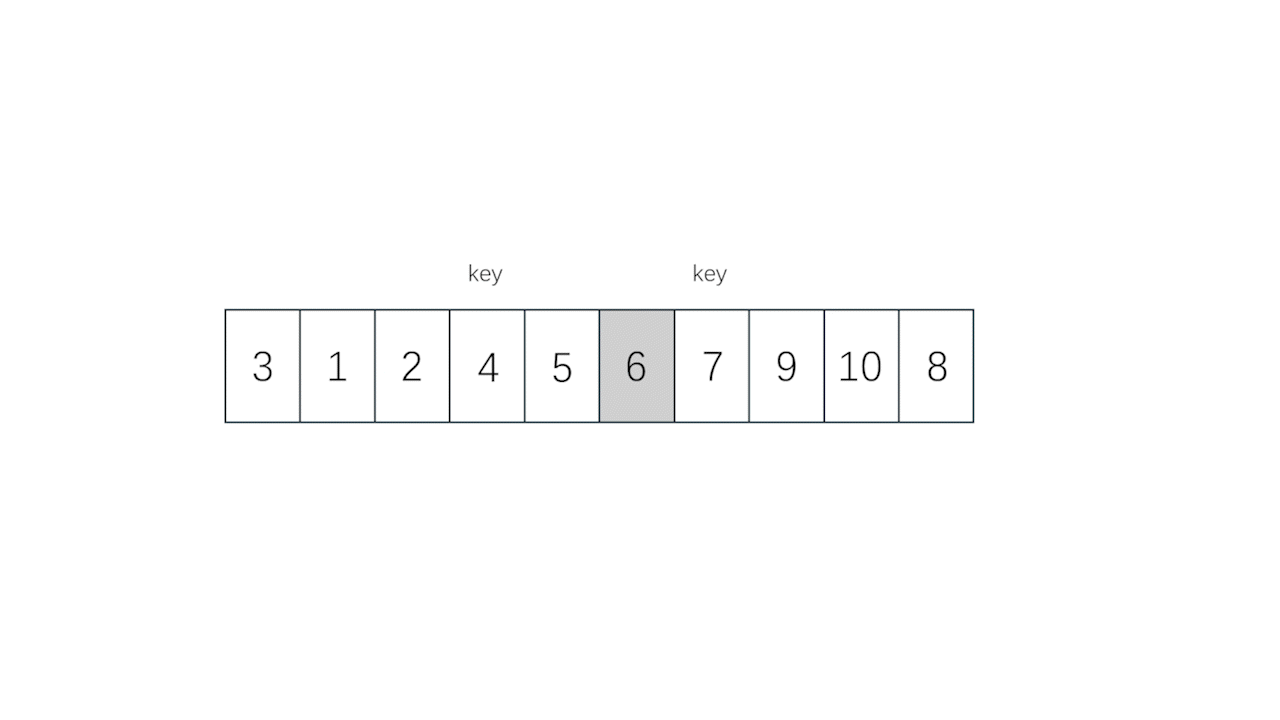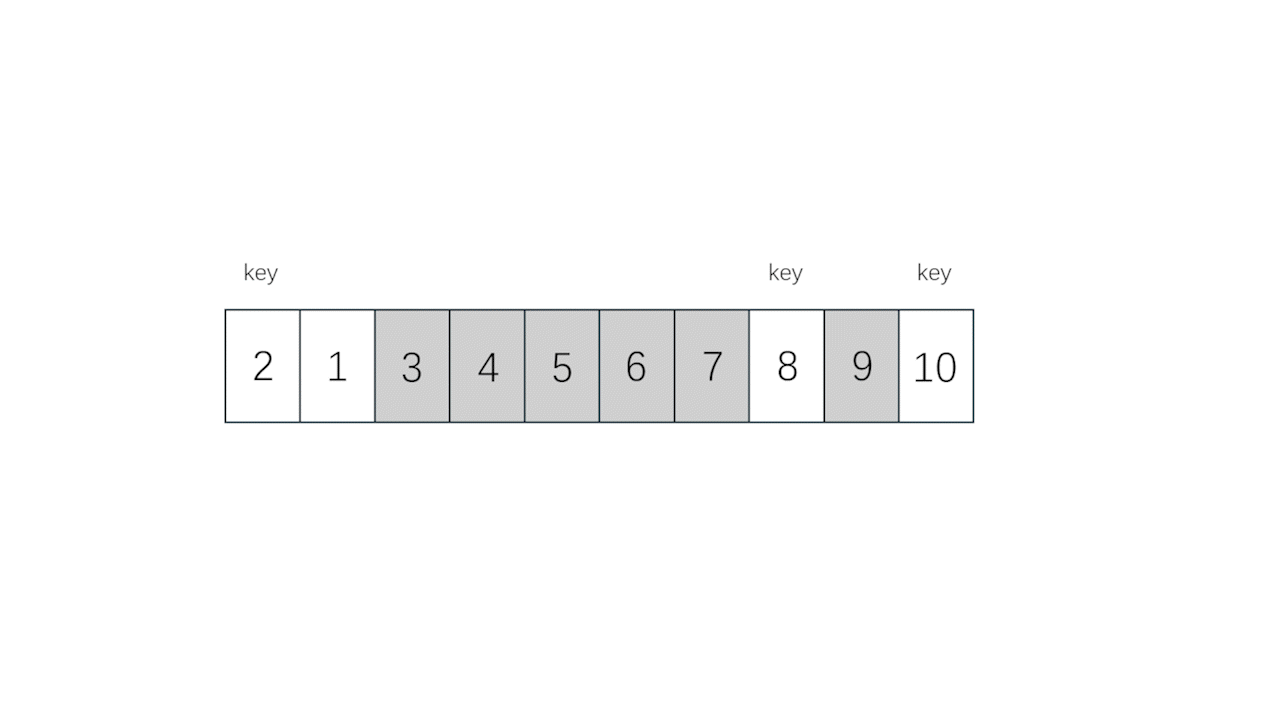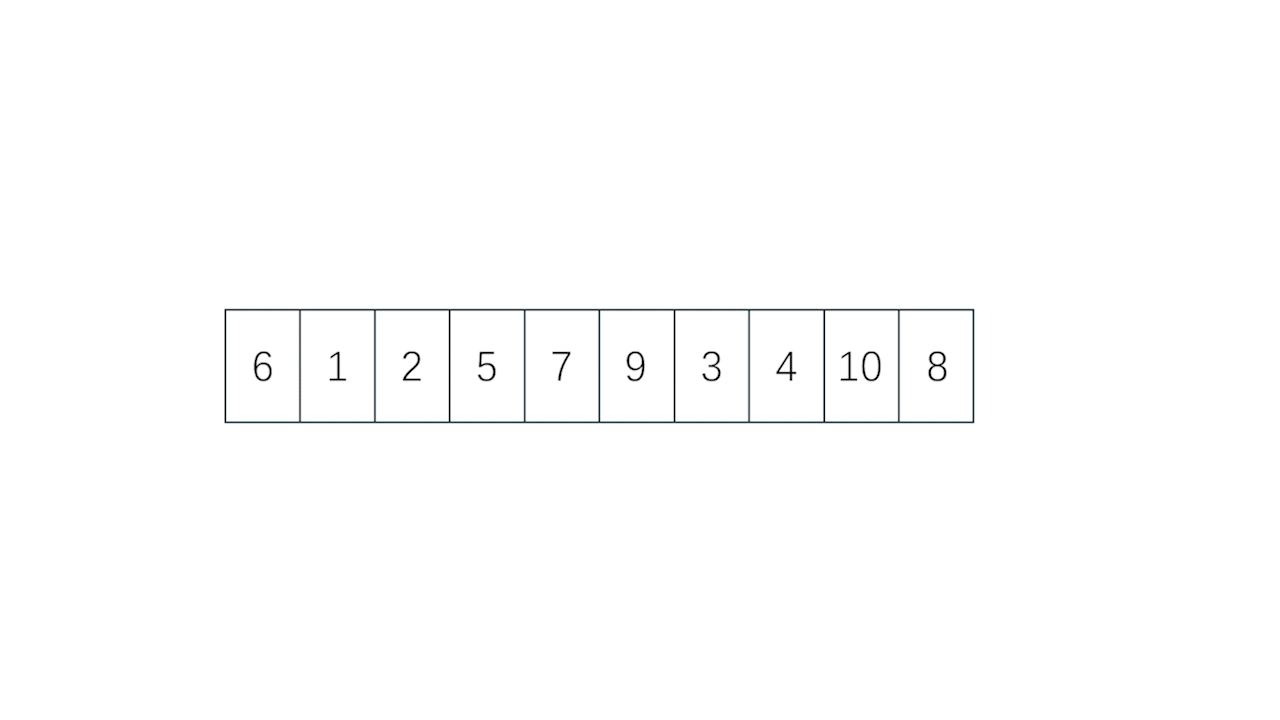
- 快速排序的基本思想为分治,即将一个大数组分为左右2个小数组,不断下分直到无法再进行下分为止
- 再具体一点,即取一个下标为 key 处,调整除了 key 处以外的剩下的值,直到 key 处的值到了它应该到的位置, key 左边的数应该全部小于等于 key , key 右边的数应该全部大于 key ,此时 key 左边的部分看作一个新的数组, key 右边的部分也看做一个新的数组,不断让新数组重复此操作,直到所有的数字全部到了它们所应该在的位置上,即排序完毕,详细可见动图
- 快速排序有很多种写法,但都离不开分治的思想,具体写法详见下文
2 霍尔版快速排序的实现
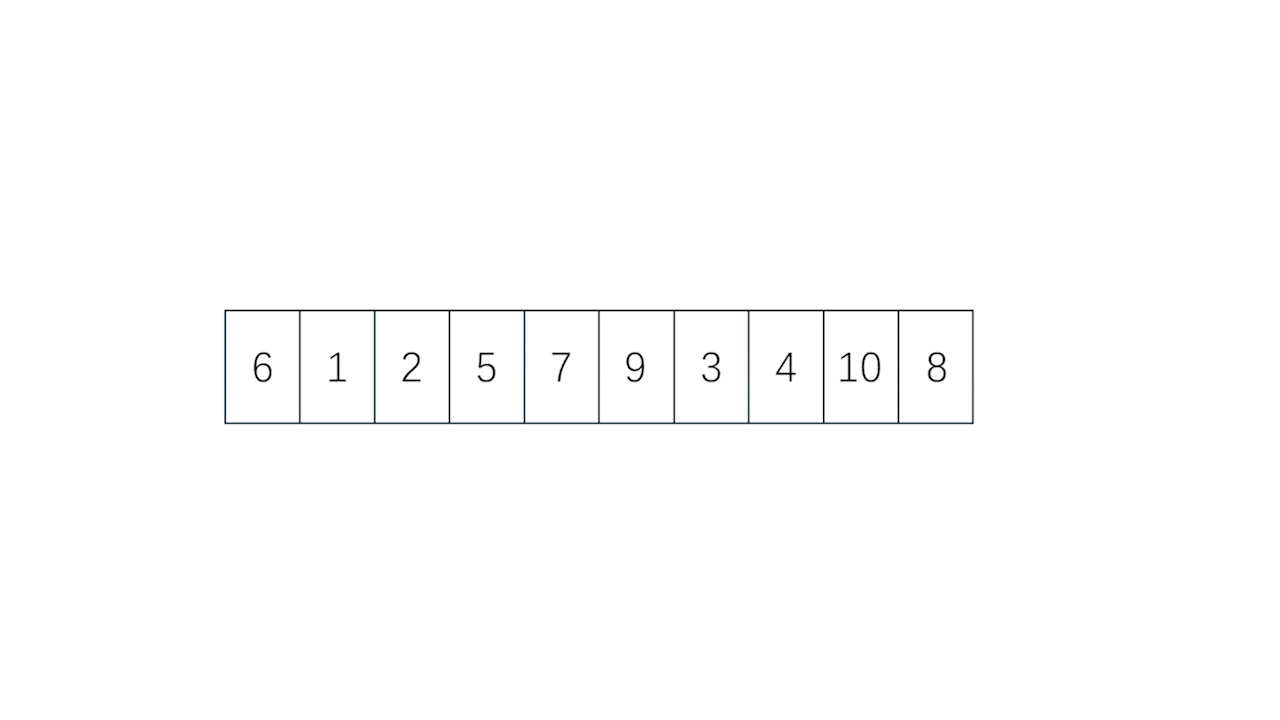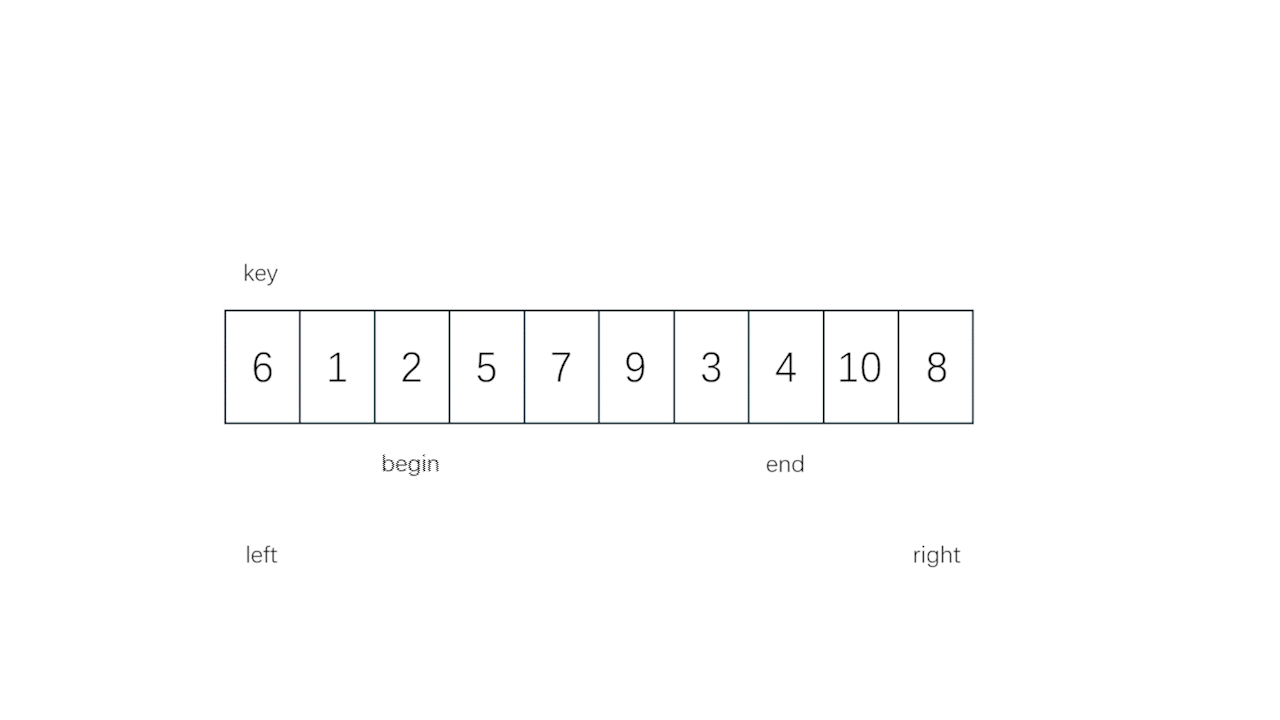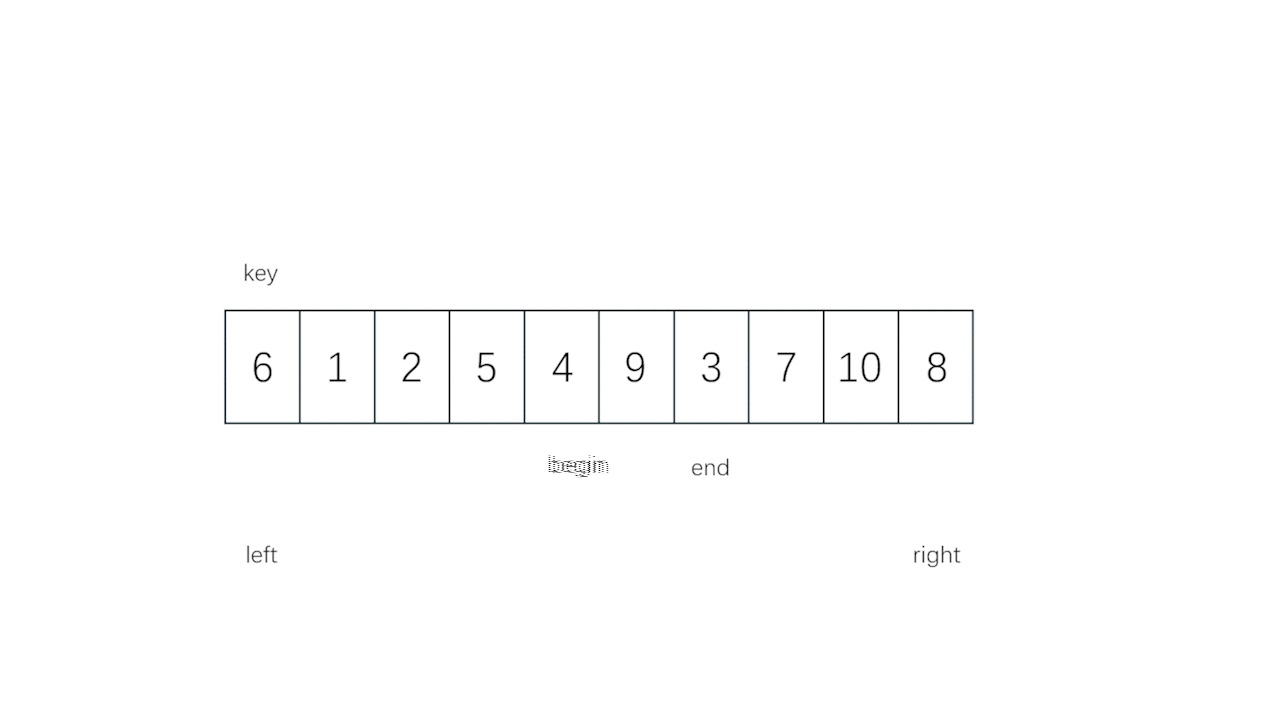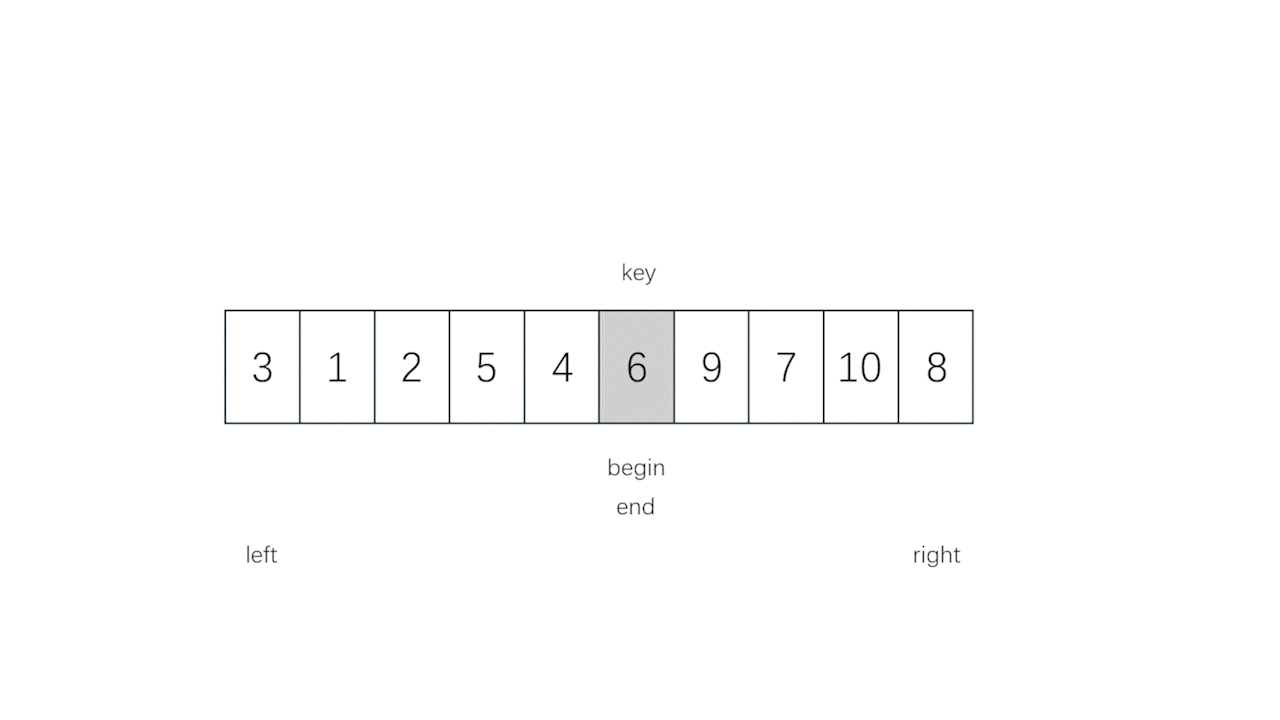
//快速排序
void QuickSort(SortType* a, int left, int right)
{
//1.key(标记数)
//2.begin(向左找比 key 大的数)
//3.end(向右找比 key 小的数)
//4.left(标记当前需要处理的数组的范围)
//5.right(标记当前需要处理的数组的范围)
assert(a); //检测指针是否为空
if (right <= left) //范围如果小于等于1,那就不需要排序,直接return
{
return;
}
int key = left; //key默认设置为最左边的数
int begin = left; //begin从最左边往右走
int end = right; //end从最右边往左走
while (begin < end)
{
//向右找小
while (begin != end && a[key] <= a[end]) //找不到就让end左走,直到找到或者相遇为止
{
end--;
}
//向左找小
while (begin != end && a[key] >= a[begin]) //找不到就让begin往右走,直到找到或者相遇为止
{
begin++;
}
Swap(&a[begin], &a[end]); //交换begin处的大数和end处的小数,如果两者相遇则自己和自己交换
}
Swap(&a[key], &a[begin]); //交换begin和key的值(此时begin一定和end相遇了)
key = begin; //交换之后key的下标要改过来
QuickSort(a, left, key - 1); //左边未排序的部分开始进行排序
QuickSort(a, key + 1, right); //左边未排序的部分开始进行排序
}
3 快速排序的基本优化方式
3.1 关于小数组的优化
- 当数组足够小的时候,快排函数此时的效率相对低了,我们就可以用插入法
//小区间优化
if (right - left + 1 <= 10)
{
InsertSort(a + left, right - left + 1);
return;
}
3.2 关于key处数字过小或者过大导致遍历整个数组的优化
- 我们假设传进函数的是一个已经排好序的数组,那么此时 end 会将整个数组全部遍历一遍, begin 将保持不动,数组并未分为两个较小的数组,分治思想在此时就不管用了,所以我们需要用一种方式防止 key 取到小数或者大数,而只取到处于中间的数,即"三数取中"
//三数取中
int GetMidi(sorttype* arr, int left, int right)
{
int midi = (left + right) / 2; //定义中间数的下标
if (arr[left] > arr[midi])
{
if (arr[right] > arr[left]) //arr[right] > arr[left] > arr[midi]
{
return left;
}
else if (arr[midi] > arr[right]) //arr[left] > arr[midi] > arr[right]
{
return midi;
}
else //其他两个都不是,只能返回right了
{
return right;
}
}
else // arr[left] < arr[midi]
{
if (arr[right] < arr[left]) //arr[right] < arr[left] < arr[midi]
{
return left;
}
else if (arr[midi] < arr[right]) //arr[left] < arr[midi] < arr[right]
{
return midi;
}
else //其他两个都不是,返回right
{
return right;
}
}
}
3.3 优化之后的快排
//快速排序
void QuickSort(SortType* a, int left, int right)
{
assert(a);
if (right <= left)
{
return;
}
//小区间优化
if (right - left + 1 <= 10)
{
InsertSort(a + left, right - left + 1);
return;
}
//三者取中
int key = GetMid(a, left, right);
int begin = left;
int end = right;
while (begin < end)
{
//向右找小
while (begin != end && a[key] <= a[end])
{
end--;
}
//向左找小
while (begin != end && a[key] >= a[begin])
{
begin++;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[key], &a[begin]);
key = begin;
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
4 快速排序为什么一定要先向右取小的讨论(重要)
4.1 霍尔版快速排序的深度解构
- 通过前面的学习我们知道了霍尔版快速排序就是用一个 key 值将一个数组向下分为两个数组,不断细分直至完成排序,接下来我们来详细解读一下 begin 和 end 在快速排序中的意义
- end 在运动的过程中伴随着几个性质
- 其一: end 在遇到begin前停下的位置一定是一个"小数"
- 其二: end 走过的地方一定是"大数"
- 同样的, begin 在运动的过程中也伴随着以下性质
- 其一: begin 在遇到 end 前停下的位置一定是一个"大数"
- 其二: begin走过的地方一定是"小数"
- 当 end 向左走的时候,遇见了"小数"便停下,他需要一个空间能存放这个原本不属于这里的"小数",于是便让 begin 出发寻找一个大数,目的是能让它俩刚好能够交换,这样就能够保证 end 走过的地方一定是"大数", begin 走过的地方一定是"小数"
- 当它们两个相遇的时候,左边是"小数区",右边是"大数区",剩下的唯一一个中间值就只能放不大且不小的 key 了
4.2 霍尔版快速排序的 key 值交换规律
- 再排完一轮之后, 放在最左边的 key 值应该挪到中间 begin 和 end 相交的位置去,于是被挪到最左边的值(相交位置的值)一定得是个"小数",否则不符合左小右大的规律,排序会失败
- begin 和 end 在挪动的最后一步中会有以下规律:
- begin 遇上 end
- end 遇上 begin
- 当 begin 遇上 end 时
- 此时因为 end 比 begin 先出发,它应该已经找到了一个"小数",而 begin 走过的地方一定是"小数区",此时 begin 遇上 end ,跟 key 交换的一定是"小数"
- 当 end 遇上 begin时
- end 先走, begin 此时还没有动,此时 begin 处的一定是上一轮交换过的数(“上一轮交换到 begin 处的一定是个’小数’ “),于是当 end 遇上 begin 的时候, 相交处一定是个"小数”(如果 begin 从来没动过, end 遇上 begin 的位置将正好是 key 的位置,相当于除了 key 以外,全场剩下的数全是"大数”, 此时 key 会和自己交换)
- 相反,如果让 begin 先走,那么相交位置一定是"大数",那么此时如果 key 初始位置在左边,就会把相交位置的这个"大数"交换到小数区的最左边位置,会直接导致排序失败,但如果 key 的初始位置在最右边,那么就没有问题
5 快速排序的其他实现方法 - 前后指针法
博主研究快排的时候,花了一个下午调试bug,死活搞不明白为啥逻辑没错也会排序失败,直到对比其他人的代码之后才明白,一定一定要先向右取小,于是有些前人认为,霍尔版的快排似乎很容易犯这样的错误,于是就有了下面的前后指针法
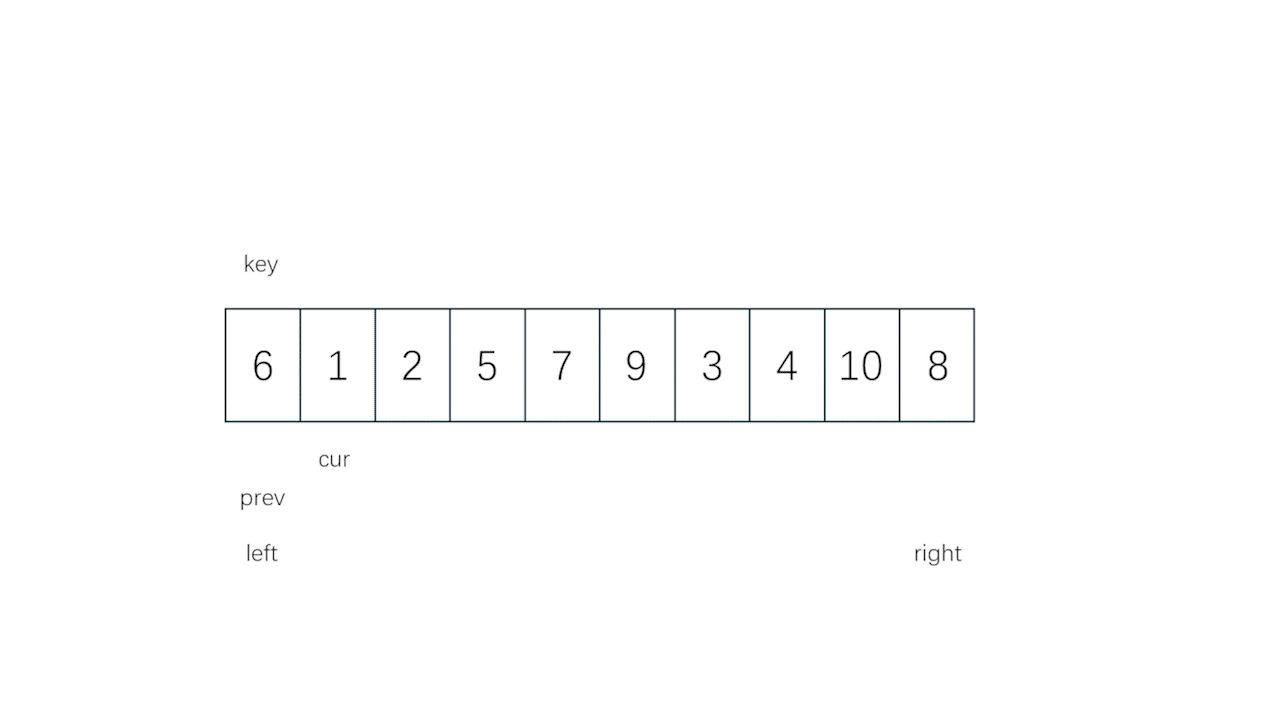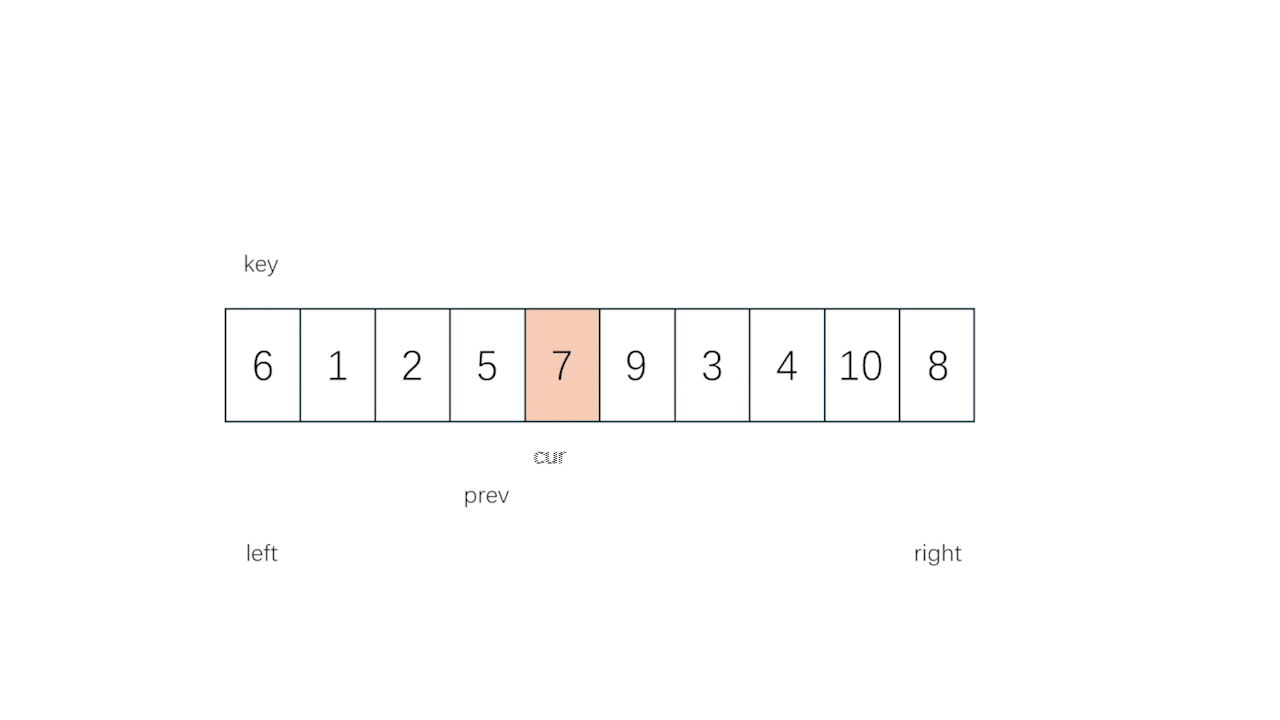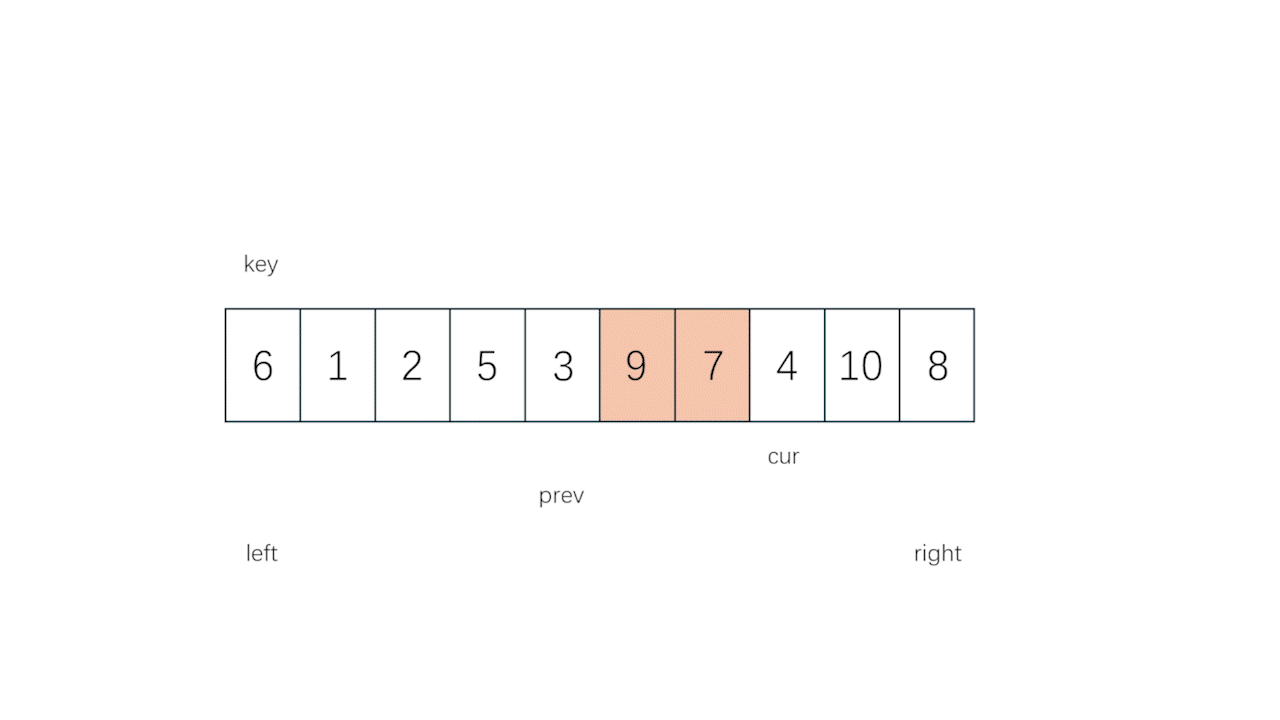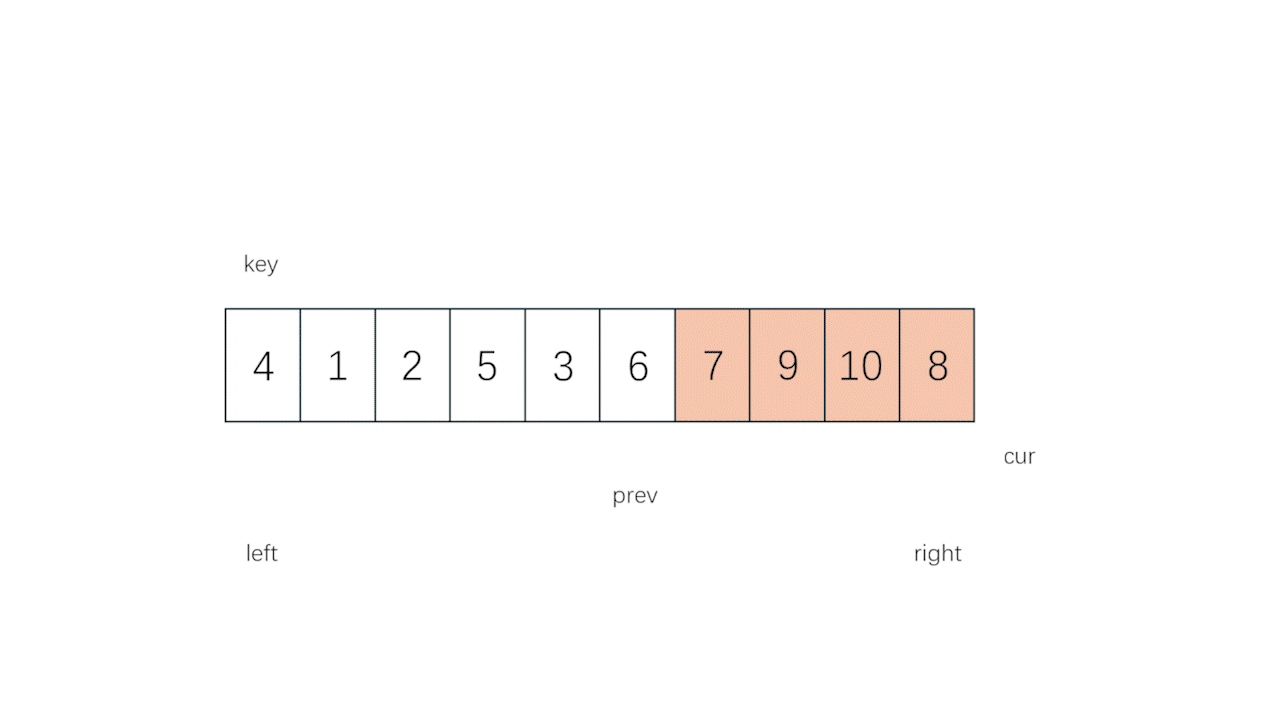
- 如果细看的话,不难发现,这个方法甚至有点像冒泡法,而区别在于冒泡法得不断遍历,每次都只冒上去一个数,而这里是一次冒很多个数,只要遇到"大数"就让它加入"大数"泡泡的队伍,遇到"小数"就让它下去,把上面的空间留给"大数"大队
- 想办法让"大数"遍历上去就完事儿了,完全不需要考虑左右相遇啥的(反正最后留给 prev 的一定是右边换过来的"小数"就是了)
//快速排序--前后指针法
void QuickSort(sorttype* arr, int left, int right)
{
assert(arr);
if (right <= left)
{
return;
}
//小区间优化
if ((right - left + 1) < 10)
{
InsertSort(arr + left, right - left + 1);
}
else
{
int midi = GetMidi(arr, left, right); //三数取中
Swap_s(&arr[midi], &arr[left]);
int key = left;
int prev = left; //慢指针
int cur = left + 1; //快指针
while (cur <= right) //快指针不能超过right的范围
{
if (arr[cur] < arr[key]) //遇到小数的时候让prev走一步(1.prev和cur重合,不交换 2.prev遇到大数,小数和大数交换)
{
prev++;
if (prev != cur) //这里加上判断重合可能可以提高一点点效率,加不加无所谓
{
Swap_s(&arr[prev], &arr[cur]);
}
}
cur++; //cur向后走一步
}
Swap_s(&arr[key], &arr[prev]); //把key放进它应该在的位置
int key = prev;
PartQSort(arr, left, key - 1);
PartQSort(arr, key + 1, right);
}
}
- 完整代码在最下面哦
佬!都看到这了,如果觉得有帮助的话一定要点赞啊佬 >v< !!!
放个卡密在这,感谢各位能看到这儿啦!
6 本篇文章代码汇总
1.霍尔版快速排序(未优化)
void QuickSort(SortType* a, int left, int right)
{
//1.key(标记数)
//2.begin(向左找比 key 大的数)
//3.end(向右找比 key 小的数)
//4.left(标记当前需要处理的数组的范围)
//5.right(标记当前需要处理的数组的范围)
assert(a); //检测指针是否为空
if (right <= left) //范围如果小于等于1,那就不需要排序,直接return
{
return;
}
int key = left; //key默认设置为最左边的数
int begin = left; //begin从最左边往右走
int end = right; //end从最右边往左走
while (begin < end)
{
//向右找小
while (begin != end && a[key] <= a[end]) //找不到就让end左走,直到找到或者相遇为止
{
end--;
}
//向左找小
while (begin != end && a[key] >= a[begin]) //找不到就让begin往右走,直到找到或者相遇为止
{
begin++;
}
Swap(&a[begin], &a[end]); //交换begin处的大数和end处的小数,如果两者相遇则自己和自己交换
}
Swap(&a[key], &a[begin]); //交换begin和key的值(此时begin一定和end相遇了)
key = begin; //交换之后key的下标要改过来
QuickSort(a, left, key - 1); //左边未排序的部分开始进行排序
QuickSort(a, key + 1, right); //左边未排序的部分开始进行排序
}
2.霍尔版快速排序(优化版)
void QuickSort(SortType* a, int left, int right)
{
assert(a);
if (right <= left)
{
return;
}
//小区间优化
if (right - left + 1 <= 10)
{
InsertSort(a + left, right - left + 1);
return;
}
//三者取中
int key = GetMid(a, left, right);
int begin = left;
int end = right;
while (begin < end)
{
//向右找小
while (begin != end && a[key] <= a[end])
{
end--;
}
//向左找小
while (begin != end && a[key] >= a[begin])
{
begin++;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[key], &a[begin]);
key = begin;
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
3.前后指针法快速排序
void QuickSort(sorttype* arr, int left, int right)
{
assert(arr);
if (right <= left)
{
return;
}
//小区间优化
if ((right - left + 1) < 10)
{
InsertSort(arr + left, right - left + 1);
}
else
{
int midi = GetMidi(arr, left, right); //三数取中
Swap_s(&arr[midi], &arr[left]);
int key = left;
int prev = left; //慢指针
int cur = left + 1; //快指针
while (cur <= right) //快指针不能超过right的范围
{
if (arr[cur] < arr[key]) //遇到小数的时候让prev走一步(1.prev和cur重合,不交换 2.prev遇到大数,小数和大数交换)
{
prev++;
if (prev != cur) //这里加上判断重合可能可以提高一点点效率,加不加无所谓
{
Swap_s(&arr[prev], &arr[cur]);
}
}
cur++; //cur向后走一步
}
Swap_s(&arr[key], &arr[prev]); //把key放进它应该在的位置
int key = prev;
PartQSort(arr, left, key - 1);
PartQSort(arr, key + 1, right);
}
}





















 5292
5292

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








