记忆化搜索题目（一）

原创已于 2025-12-01 20:28:15 修改 · 228 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #深度优先 #leetcode #c语言 #c++

于 2025-12-01 20:27:22 首次发布

算法题目专栏收录该内容

57 篇文章

订阅专栏

一：斐波那契数列

1.1题目

题目链接：https://leetcode.cn/problems/fibonacci-number/description/

1.2算法原理

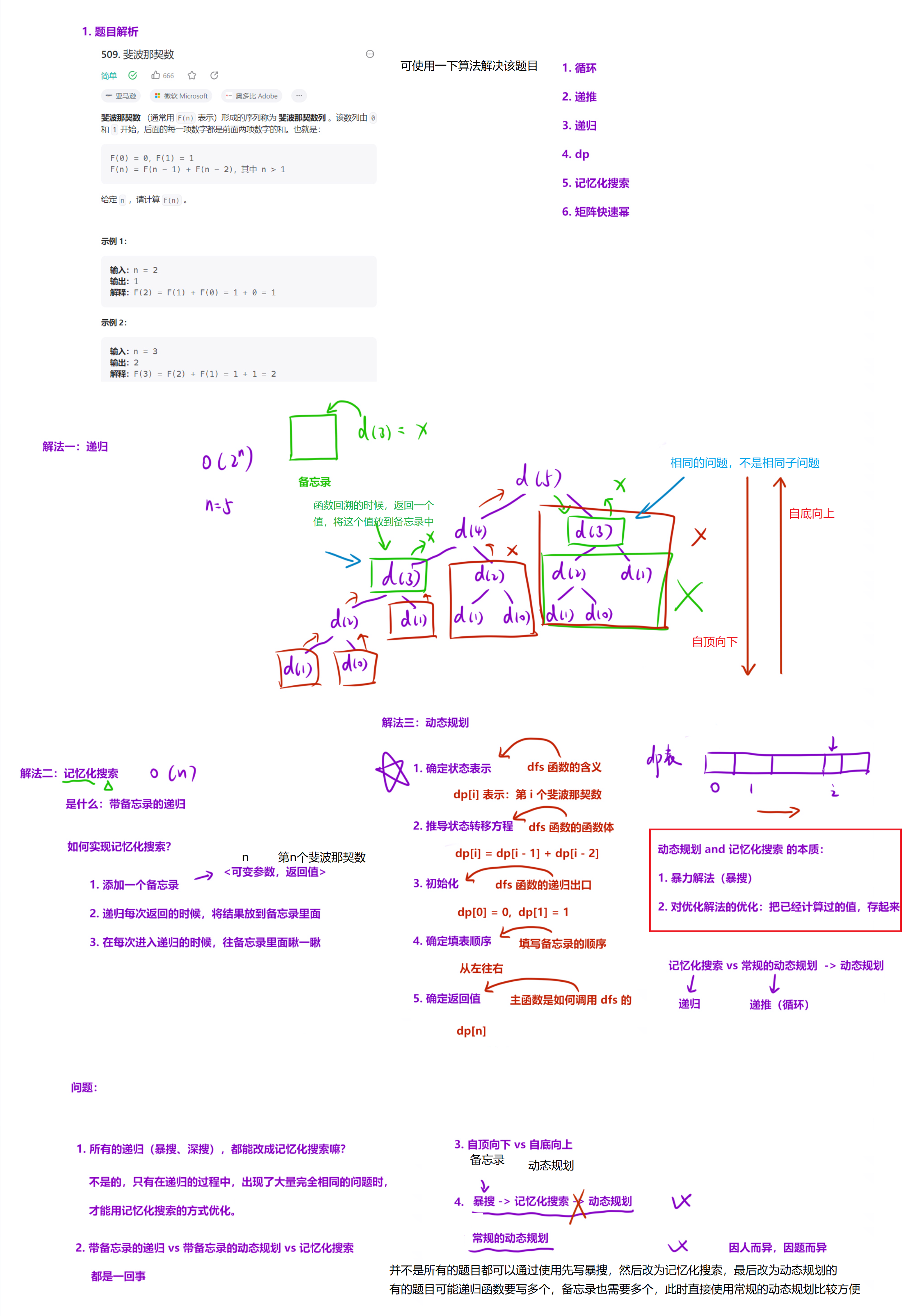
1.3代码

递归版本：

class Solution {
public:
    int fib(int n) 
    {
        return dfs(n);
    }

    int dfs(int n)
    {
       if(n == 0 || n == 1)    return n;

        return dfs(n-1)+dfs(n-2);  
    }
};

记忆化搜索版本：

class Solution {
public:
    int memory[31];
    int fib(int n) 
    {
        //初始化，保证memory和数列里面的值不会相等
        memset(memory,-1, sizeof(memory));
        return dfs(n);
    }

    int dfs(int n)
    {
        if(memory[n] != -1) return memory[n];
        if(n == 0 || n == 1)
        {
            memory[n] = n;
            return n;
        }

        memory[n] = dfs(n-1)+dfs(n-2);
        return memory[n];  
    }
};

动态规划：

class Solution {
public:
    int dp[31];
    int fib(int n) 
    {
        dp[0] = 0, dp[1] = 1;
        for(int i = 2; i<= n;i++)
            dp[i] = dp[i-1]+dp[i-2];
        return dp[n];    
    }
};

二：不同的路径

2.1题目

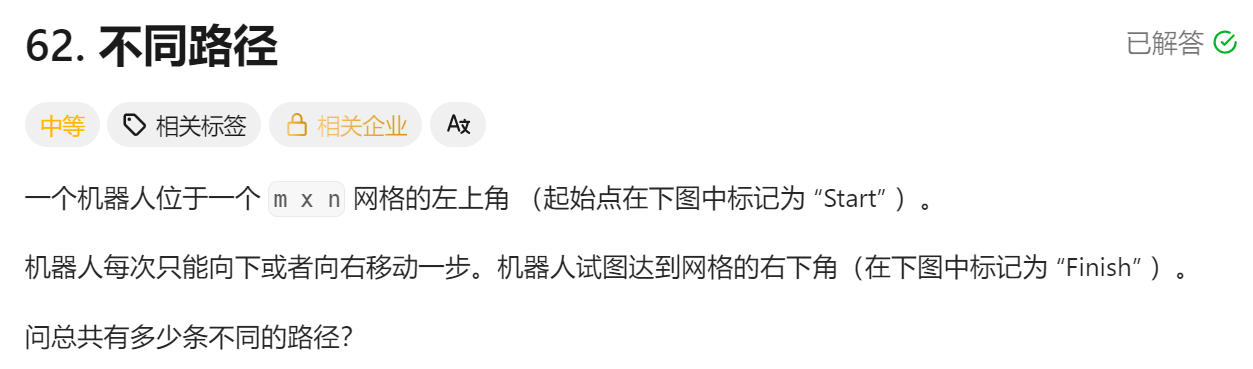
题目链接： https://leetcode.cn/problems/unique-paths/description/

2.2算法原理

2.3代码

递归版本：超时

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        return dfs(m,n);    
    }

    int dfs(int i, int j)
    {
        if(i == 0 || j == 0) return 0;
        if(i == 1 && j == 1) return 1;

        return dfs(i-1,j)+dfs(i,j-1);
    }
};

记忆化搜索：

class Solution {
public:
    vector<vector<int>> memory;
    int uniquePaths(int m, int n) 
    {
        memory = vector<vector<int>>(m+1,vector<int>(n+1));
        return dfs(m,n);    
    }

    int dfs(int i, int j)
    {
        if(memory[i][j])
            return memory[i][j];

        if(i == 0 || j == 0) return 0;
        if(i == 1 && j == 1)
        {
            memory[i][j] = 1;
            return memory[i][j];
        }

        memory[i][j] = dfs(i-1,j)+dfs(i,j-1);

        return memory[i][j];
    }
};

动态规划：

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
       vector<vector<int>> dp(m+1,vector<int>(n+1));
       dp[1][1] = 1;
       for(int i = 1; i <= m; i++)
            for(int j = 1; j <= n;j++)
            {
                if(i == 1 && j == 1) continue;
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }    

        return dp[m][n];
    }

};