1.学习大纲与考点

2.查找的优劣性评估

定义:
查找的过程是将给定的 关键字值 与文件中各记录的关键字项进行比较的过程。因此,用比较次数的平均值来评价算法的优劣,称为平均查找长度(ASL, Average Search Length)。
ASL公式:
ASL=∑i=1npi⋅Ci ASL = \sum_{i=1}^n p_i \cdot C_i ASL=i=1∑npi⋅Ci
其中:
- n:文件记录的个数。
- p_i:查找到第 (i) 个记录的查找概率(通常取等概率,(p_i = 1/n))。
- C_i:查找到第 (i) 个记录时所经历的比较次数。
物理意义:
假设每个元素被查找的概率相同,则查找每一元素所需的比较次数总和再取平均,即为 ASL。
总结:
- ASL 表示统计意义上的数学期望值。
- ASL值越小,时间效率越高。
-典型例题
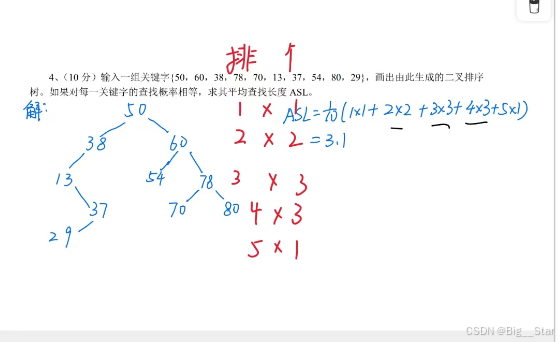
3.顺序查找表
顺序查找的算法实现如下:
int search (int* a,int n,int key)
{
int i;
for(int i = 0; i <= n; i++)
{
if(a[i] == key)
return i;
}
return 0;
}
不过这个算法存在了一些缺点,因为每次循环都要检测i是否越界,即代码段 i<=n.
鉴于此,我们设定带哨兵位置的优化。
int search_optimization ( int* a,int n; int key)
{
int i;
a[0] = key //此处为设置哨兵位置
i = n;//放到队尾
while (a[n] == key)
{
i--;
}
return i;
}
4.静态查找-折半查找
折半查找又称为二分查找,他的前提是线性表有顺序。
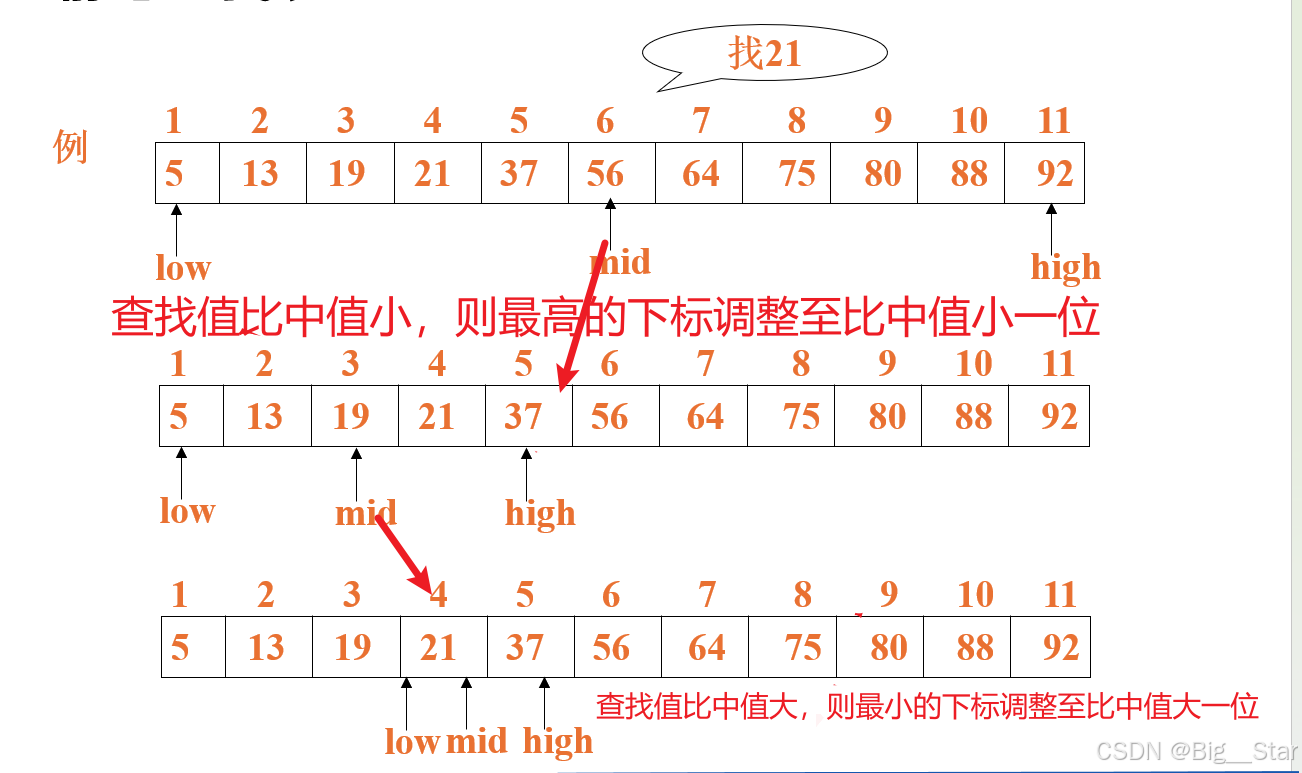
int binary search( int* a, int i ,int key)
{
int low,mid,high;
low = 1 ;
high = n;
while (low <= high)
{
mid = (low+high) / 2;
if(key < a[mid])
high = mid - 1;
else if (key >= a[mid])
low = mid + 1;
else
return mid;
}
return 0;
5.动态查找-二叉排序树

首先我们提供一个二叉树的结构
typedef struct BiTNode
{
int data;
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree
下面我们来写一个二叉排序树的查找算法
Status SearchBST (BiTree T, int key, BiTree f,BiTree *p)
//初次调用时,T 通常是整棵树的根节点。
// f为存储的父节点信息。
//p 用于返回结果指针。
{
if(!T)//空树或递归到空节点
{
*p = f;
return FALSE;
}
else if (key == T->data)
{
*p = T;
return True;
}
else if (key < T->data)
return SearchBST(T->lchild,key,T,p);
else
return SearchBST(T->rchild,key,T,p);
}
有了二叉排序树的查找,插入算法就是把关键字放到合适的位置。
问:如果存在相同值怎么办?
答:抽象为集合,利用集合的性质没有重复元素。
Status InsertBST(BiTree *T,int key)
{
BiTree p,s;
if( !SearchBST(*T,key,NULL,&p)
{//调用 SearchBST 查找关键字 key,如果不存在先开辟空间。
s = (BiTree)malloc(sizeof(BiTNode));
s->data = key;
s->lchild = s->rchild =NULL;
if (!p)
*T = s;
else if (key < p->data)
p->lchild = s;
else
p->rchild = s;
return TRUE;
}
else
return FALSE;
}
数据结构删除在LNTU不做要求…
详见其他博客推送。
6.平衡二叉树

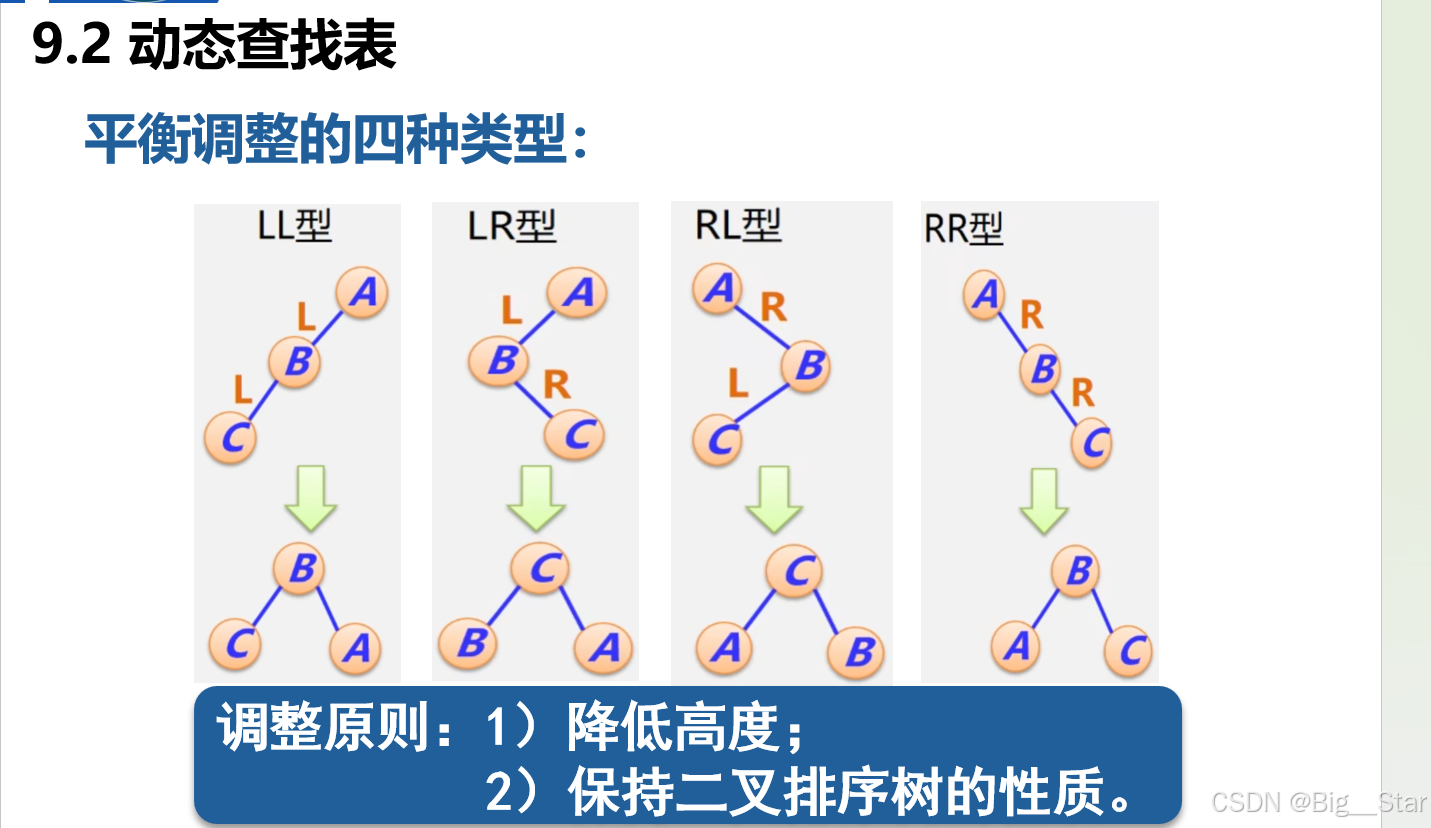
LNTU的平衡树考点详见例题(貌似不考察代码)
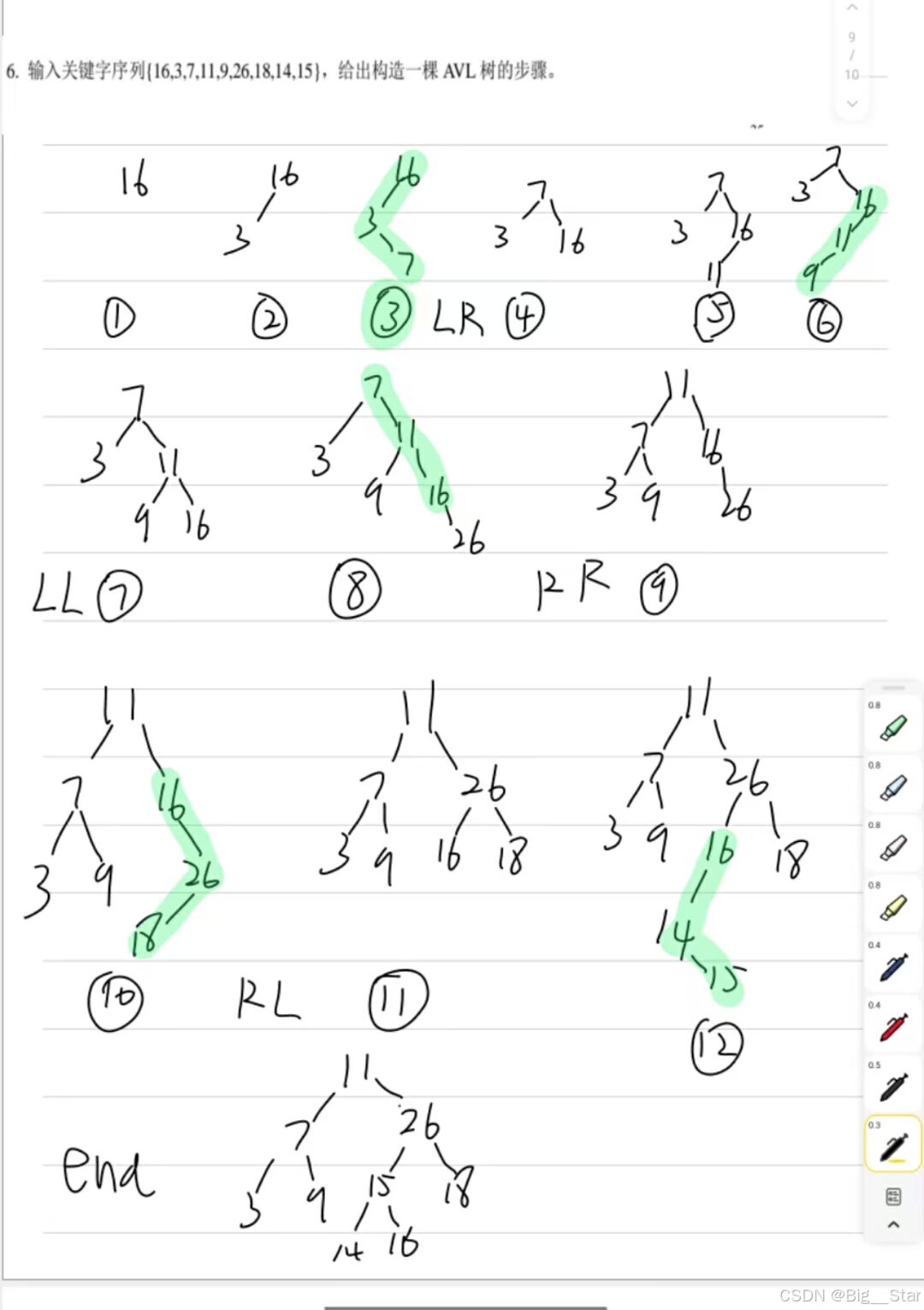
ps:询问过老师,考试可以不写平衡因子。
7.哈希表
LNTU不对哈希表的代码进行考察…
在此本文通过开放定址线性探测、二次探测在散列、链地址法详细介绍考点。
7.1 考点一 哈希表探测法构造
注意:表长取素数。

7.2考点2 哈希表二次探测及其链表法





















 71
71

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








