数据变换与偏度校正：从 Ames 房价数据集看数据正态化实践

原创 于 2025-10-27 10:15:55 发布 · 812 阅读 · 17 ·
CC 4.0 BY-SA版权
原创文章，禁止转载，否则保留追究法律责任的权利。
文章标签：

#数据变换 #偏度校正 #数据正态化 #Box-Cox #Yeo-Johnson #KS检验 #特征工程

【精选优质专栏推荐】


每个专栏均配有案例与图文讲解，循序渐进，适合新手与进阶学习者，欢迎订阅。

文章目录

在这里插入图片描述

前言

数据转换使数据科学家能够将原始数据精炼、规范化并标准化为适合分析的格式。这些转换不仅是过程步骤，更是减轻偏差、处理偏态分布、增强统计模型稳健性的重要环节。

本章主要讨论如何处理偏态数据。通过关注 Ames 房价数据集中的 “SalePrice” 与 “YearBuilt” 属性，你将看到正偏与负偏数据的示例，以及如何通过不同转换方法将其分布正态化。

理解偏度与转换的必要性

偏度（Skewness）是一个描述数据分布相对于均值是否对称的统计指标。简单来说，它表示数据是否集中在分布的一侧，而另一侧拖出较长的尾巴。

在数据分析中通常会遇到两种偏度类型：

1.正偏（Positive Skewness）：
当分布的尾部向较高数值（峰值右侧）延伸时出现。数据主要集中在较低端，表示大多数值较小，但存在少量极高值。

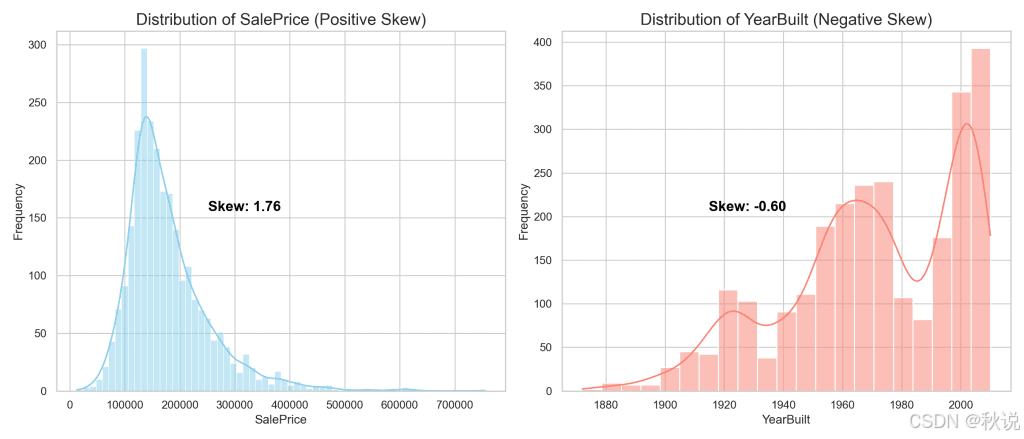
在 Ames 数据集中，“SalePrice” 属性表现出明显的正偏——多数房屋售价较低，但少数房屋价格显著偏高。

2.负偏（Negative Skewness）：
当分布的尾部向较低数值（峰值左侧）延伸时出现。此时数据集中在较高端，较少的值拖向低端。

在 Ames 数据集中，“YearBuilt” 属性体现出负偏——大多数房屋建于较近年份，少部分为较早期建筑。

为更好地理解这些概念，下面进行可视化示例：

# 导入必要库
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import boxcox, yeojohnson
from sklearn.preprocessing import QuantileTransformer

# 载入数据集
Ames = pd.read_csv('Ames.csv')

# 计算偏度
sale_price_skew = Ames['SalePrice'].skew()
year_built_skew = Ames['YearBuilt'].skew()

# 设置Seaborn样式
sns.set(style='whitegrid')

# 创建包含两个子图的画布
fig, ax = plt.subplots(1, 2, figsize=(14, 6))

# SalePrice（正偏）分布图
sns.histplot(Ames['SalePrice'], kde=True, ax=ax[0], color='skyblue')
ax[0].set_title('SalePrice 分布（正偏）', fontsize=16)
ax[0].set_xlabel('SalePrice')
ax[0].set_ylabel('Frequency')
ax[0].text(0.5, 0.5, f'Skew: {sale_price_skew:.2f}', transform=ax[0].transAxes,
           horizontalalignment='right', color='black', weight='bold', fontsize=14)

# YearBuilt（负偏）分布图
sns.histplot(Ames['YearBuilt'], kde=True, ax=ax[1], color='salmon')
ax[1].set_title('YearBuilt 分布（负偏）', fontsize=16)
ax[1].set_xlabel('YearBuilt')
ax[1].set_ylabel('Frequency')
ax[1].text(0.5, 0.5, f'Skew: {year_built_skew:.2f}', transform=ax[1].transAxes,
           horizontalalignment='right', color='black', weight='bold', fontsize=14)

plt.tight_layout()
plt.show()

在 “SalePrice” 图中，可以看到明显的右偏分布，这种偏态给建模带来挑战，可能掩盖真实规律，导致预测误差。

相对地，“YearBuilt” 呈现左偏分布，表明新建房屋数量占多数，而老旧房屋形成了左侧的长尾。

在这里插入图片描述

通过数据转换来处理偏态不仅是统计层面的调整，更是获得精确且可操作性洞察的重要步骤。

应用这些转换的目标在于减弱偏度的影响，从而提升分析结果的可靠性与可解释性。

这种正态化过程让数据科学分析更具意义，不仅满足统计要求，也体现出对数据质量与可用性的改进追求，为后续的数据转换探索奠定基础。

处理正偏数据的策略

为应对正偏分布（Positive Skewness），常用的五种转换方法如下：

  1. 对数转换（Log Transformation）
  2. 平方根转换（Square Root Transformation）
  3. Box-Cox 转换
  4. Yeo-Johnson 转换
  5. 分位数转换（Quantile Transformation）

每种方法都旨在降低偏度，使数据更适合进一步分析。

1. 对数转换（Log Transformation）

该方法特别适用于右偏数据。

通过对数据取自然对数，压缩数值范围，减少大数值间的差距，使分布更平滑。

# 对数转换
Ames['Log_SalePrice'] = np.log(Ames['SalePrice'])
print(f"Skewness after Log Transformation: {Ames['Log_SalePrice'].skew():.5f}")

输出结果：

Skewness after Log Transformation: 0.04172

说明偏度大幅降低。

2. 平方根转换（Square Root Transformation）

此方法较对数转换温和，适合中度偏态数据。

通过对每个数据取平方根，可降低偏度并减少异常值影响，使分布更对称。

# 平方根转换
Ames['Sqrt_SalePrice'] = np.sqrt(Ames['SalePrice'])
print(f"Skewness after Square Root Transformation: {Ames['Sqrt_SalePrice'].skew():.5f}")

输出：

Skewness after Square Root Transformation: 0.90148

3. Box-Cox 转换

Box-Cox 通过优化参数 λ（lambda）来确定最佳幂次转换，仅适用于正值数据。

此方法能系统性地减少偏度并稳定方差，使数据更接近正态分布。

# 在确保数据全为正值后应用 Box-Cox 转换
if (Ames['SalePrice'] > 0).all():
    Ames['BoxCox_SalePrice'], _ = boxcox(Ames['SalePrice'])
else:
    print("存在非正数值，请使用 Yeo-Johnson 或其他方法。")

print(f"Skewness after Box-Cox Transformation: {Ames['BoxCox_SalePrice'].skew():.5f}")

输出：

Skewness after Box-Cox Transformation: -0.00436

偏度几乎为零，是目前最优的转换结果。

4. Yeo-Johnson 转换

前述几种转换仅适用于正值数据。

Yeo-Johnson 是 Box-Cox 的扩展版本，能同时处理正值与非正值。

它通过优化参数 λ 调整数据形态，更适应各种范围的数据分布。

# Yeo-Johnson 转换
Ames['YeoJohnson_SalePrice'], _ = yeojohnson(Ames['SalePrice'])
print(f"Skewness after Yeo-Johnson Transformation: {Ames['YeoJohnson_SalePrice'].skew():.5f}")

输出：

Skewness after Yeo-Johnson Transformation: -0.00437

结果与 Box-Cox 接近，同样实现了高度对称分布。

5. 分位数转换（Quantile Transformation）

分位数转换通过将数据映射到指定分布（如正态分布），强制性地调整数据分布，使其形状接近高斯分布。

该方法非线性且不可逆，但能显著消除偏度。

# 应用分位数转换，使数据服从正态分布
quantile_transformer = QuantileTransformer(output_distribution='normal', random_state=0)
Ames['Quantile_SalePrice'] = quantile_transformer.fit_transform(Ames['SalePrice'].values.reshape(-1, 1)).flatten()
print(f"Skewness after Quantile Transformation: {Ames['Quantile_SalePrice'].skew():.5f}")

输出：

Skewness after Quantile Transformation: 0.00286

由于该方法直接强制数据符合正态分布，偏度最接近零。

可视化比较各方法的效果

# 绘制转换前后 SalePrice 分布图
fig, axes = plt.subplots(2, 3, figsize=(18, 15))
axes = axes.flatten()

for ax in axes[6:]:
    ax.axis('off')

# 原始分布
sns.histplot(Ames['SalePrice'], kde=True, bins=30, color='skyblue', ax=axes[0])
axes[0].set_title('原始 SalePrice 分布 (Skew: 1.76)')
axes[0].set_xlabel('SalePrice')
axes[0].set_ylabel('Frequency')

# 对数转换
sns.histplot(Ames['Log_SalePrice'], kde=True, bins=30, color='blue', ax=axes[1])
axes[1].set_title('对数转换后 (Skew: 0.04172)')

# 平方根转换
sns.histplot(Ames['Sqrt_SalePrice'], kde=True, bins=30, color='orange', ax=axes[2])
axes[2].set_title('平方根转换后 (Skew: 0.90148)')

# Box-Cox 转换
sns.histplot(Ames['BoxCox_SalePrice'], kde=True, bins=30, color='red', ax=axes[3])
axes[3].set_title('Box-Cox 转换后 (Skew: -0.00436)')

# Yeo-Johnson 转换
sns.histplot(Ames['YeoJohnson_SalePrice'], kde=True, bins=30, color='purple', ax=axes[4])
axes[4].set_title('Yeo-Johnson 转换后 (Skew: -0.00437)')

# 分位数转换
sns.histplot(Ames['Quantile_SalePrice'], kde=True, bins=30, color='green', ax=axes[5])
axes[5].set_title('分位数转换后 (Skew: 0.00286)')

plt.tight_layout(pad=4.0)
plt.show()

该可视化展示了 “SalePrice” 在应用不同转换前后的分布差异。

通过对比，我们可以直观看出各方法在缓解偏度、改善数据对称性方面的效果。

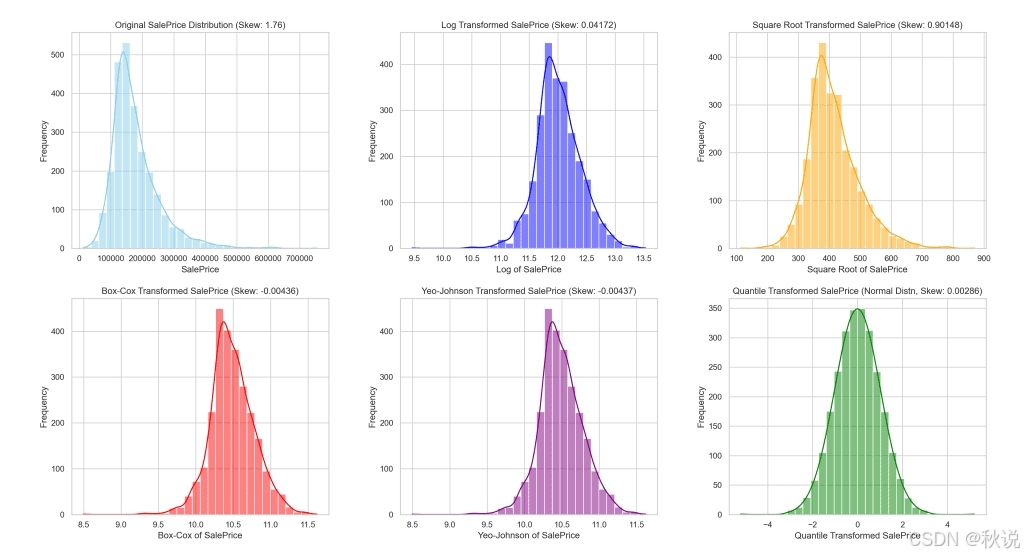
在这里插入图片描述

该可视化清楚展示了每种转换方法如何改变 “SalePrice” 的分布形态，以及它们在实现更接近正态分布方面的效果。

处理负偏数据的策略

为应对负偏分布（Negative Skewness），可采用以下五种主要转换方法：

  1. 平方转换（Squared Transformation）
  2. 立方转换（Cubed Transformation）
  3. Box-Cox 转换
  4. Yeo-Johnson 转换
  5. 分位数转换（Quantile Transformation）

这些方法的目标均是减轻偏度，使数据更适合后续统计建模与分析。

1. 平方转换（Squared Transformation）

平方转换通过将数据集中的每个值平方（即提升至 2 次幂）来实现。

该方法适用于所有数据为正、负偏程度不严重的情况，因为它会扩展较低数值的差异，从而减少左偏。

# 平方转换
Ames['Squared_YearBuilt'] = Ames['YearBuilt'] ** 2
print(f"Skewness after Squared Transformation: {Ames['Squared_YearBuilt'].skew():.5f}")

输出：

Skewness after Squared Transformation: -0.57207

偏度得到改善，但仍未完全消除。

2. 立方转换（Cubed Transformation）

立方转换将每个数据点取三次幂。

与平方转换相比，它更激进地扩展低值部分，因此对偏度更大的分布更有效。

# 立方转换
Ames['Cubed_YearBuilt'] = Ames['YearBuilt'] ** 3
print(f"Skewness after Cubed Transformation: {Ames['Cubed_YearBuilt'].skew():.5f}")

输出：

Skewness after Cubed Transformation: -0.54539

偏度略有进一步改善。

3. Box-Cox 转换

Box-Cox 是一种灵活的幂次转换方法，仅适用于正值数据。

通过优化参数 λ（lambda），Box-Cox 能有效减少负偏，使数据趋于对称。

# 应用 Box-Cox 转换（需确认所有值为正）
if (Ames['YearBuilt'] > 0).all():
    Ames['BoxCox_YearBuilt'], _ = boxcox(Ames['YearBuilt'])
else:
    print("存在非正数值，请使用 Yeo-Johnson 或其他方法。")

print(f"Skewness after Box-Cox Transformation: {Ames['BoxCox_YearBuilt'].skew():.5f}")

输出：

Skewness after Box-Cox Transformation: -0.12435

偏度显著接近零，分布更对称。

4. Yeo-Johnson 转换

Yeo-Johnson 是 Box-Cox 的推广版本，可同时处理正值与负值数据。

对于负偏分布，Yeo-Johnson 能在保留数据特征的同时实现分布正态化。

# 应用 Yeo-Johnson 转换
Ames['YeoJohnson_YearBuilt'], _ = yeojohnson(Ames['YearBuilt'])
print(f"Skewness after Yeo-Johnson Transformation: {Ames['YeoJohnson_YearBuilt'].skew():.5f}")

输出：

Skewness after Yeo-Johnson Transformation: -0.12435

结果与 Box-Cox 类似，偏度趋近零。

5. 分位数转换（Quantile Transformation）

分位数转换通过根据数据的分位数将其映射到指定分布（如正态分布）。

该方法不依赖原始分布形状，对异常值鲁棒性强，可有效消除偏度并均衡数据。

# 应用分位数转换，使数据服从正态分布
quantile_transformer = QuantileTransformer(output_distribution='normal', random_state=0)
Ames['Quantile_YearBuilt'] = quantile_transformer.fit_transform(Ames['YearBuilt'].values.reshape(-1, 1)).flatten()
print(f"Skewness after Quantile Transformation: {Ames['Quantile_YearBuilt'].skew():.5f}")

输出：

Skewness after Quantile Transformation: 0.02713

偏度几乎为零，表明该方法实现了最佳的正态化效果。

可视化各方法效果

# 绘制 YearBuilt 各转换结果的分布
fig, axes = plt.subplots(2, 3, figsize=(18, 15))
axes = axes.flatten()

# 原始分布
sns.histplot(Ames['YearBuilt'], kde=True, bins=30, color='skyblue', ax=axes[0])
axes[0].set_title(f'原始 YearBuilt 分布 (Skew: {Ames["YearBuilt"].skew():.5f})')
axes[0].set_xlabel('YearBuilt')
axes[0].set_ylabel('Frequency')

# 平方转换
sns.histplot(Ames['Squared_YearBuilt'], kde=True, bins=30, color='blue', ax=axes[1])
axes[1].set_title(f'平方转换后 (Skew: {Ames["Squared_YearBuilt"].skew():.5f})')

# 立方转换
sns.histplot(Ames['Cubed_YearBuilt'], kde=True, bins=30, color='orange', ax=axes[2])
axes[2].set_title(f'立方转换后 (Skew: {Ames["Cubed_YearBuilt"].skew():.5f})')

# Box-Cox 转换
sns.histplot(Ames['BoxCox_YearBuilt'], kde=True, bins=30, color='red', ax=axes[3])
axes[3].set_title(f'Box-Cox 转换后 (Skew: {Ames["BoxCox_YearBuilt"].skew():.5f})')

# Yeo-Johnson 转换
sns.histplot(Ames['YeoJohnson_YearBuilt'], kde=True, bins=30, color='purple', ax=axes[4])
axes[4].set_title(f'Yeo-Johnson 转换后 (Skew: {Ames["YeoJohnson_YearBuilt"].skew():.5f})')

# 分位数转换
sns.histplot(Ames['Quantile_YearBuilt'], kde=True, bins=30, color='green', ax=axes[5])
axes[5].set_title(f'分位数转换后 (Skew: {Ames["Quantile_YearBuilt"].skew():.5f})')

plt.tight_layout(pad=4.0)
plt.show()

此图直观展示了 “YearBuilt” 在应用不同转换前后的分布变化，帮助我们清晰理解各方法对负偏数据对称性改善的影响与程度。

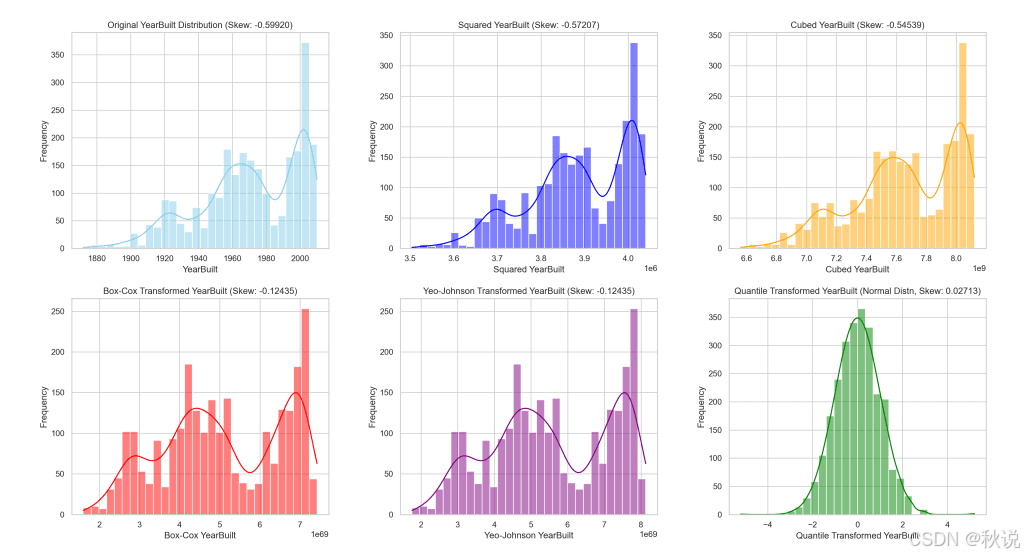
在这里插入图片描述

该可视化图清晰展示了每种变换方法如何改变 “YearBuilt” 的分布，并说明了其在实现更接近正态分布方面的效果。

如何判断变换后的数据是否符合正态分布

Kolmogorov-Smirnov（KS）检验是一种非参数检验方法，用于判断样本是否来自特定分布的总体。与假设数据服从特定分布（通常是正态分布）的参数检验不同，非参数检验不做此假设，因此在数据变换后用于评估正态性时非常有用。

KS 检验通过比较样本的累积分布函数（CDF）与参考分布（此处为正态分布）的 CDF 之间的差异，计算出一个统计量来量化两者的最大距离。

假设：

  • 零假设（𝐻₀）：数据服从指定分布（正态分布）。
  • 备择假设（𝐻₁）：数据不服从指定分布。

检验结果中的 KS 统计量代表经验分布与理论分布之间的最大偏差，值越小表示数据越接近正态分布。

代码示例

from scipy.stats import kstest

transformations = [
    "Log_SalePrice", "Sqrt_SalePrice", "BoxCox_SalePrice",
    "YeoJohnson_SalePrice", "Quantile_SalePrice",
    "Squared_YearBuilt", "Cubed_YearBuilt", "BoxCox_YearBuilt",
    "YeoJohnson_YearBuilt", "Quantile_YearBuilt"
]

ks_test_results = {}
for transformation in transformations:
    standardized_data = (Ames[transformation] - Ames[transformation].mean()) / Ames[transformation].std()
    ks_stat, ks_p_value = kstest(standardized_data, 'norm')
    ks_test_results[transformation] = (ks_stat, ks_p_value)

ks_test_results_df = pd.DataFrame.from_dict(ks_test_results, orient='index', columns=['KS Statistic', 'P-Value'])
print(ks_test_results_df.round(5))

输出结果：

变量KS StatisticP-Value
Log_SalePrice0.042610.00017
Sqrt_SalePrice0.076890.00000
BoxCox_SalePrice0.042940.00014
YeoJohnson_SalePrice0.042940.00014
Quantile_SalePrice0.007190.99924
Squared_YearBuilt0.116610.00000
Cubed_YearBuilt0.116660.00000
BoxCox_YearBuilt0.111440.00000
YeoJohnson_YearBuilt0.111440.00000
Quantile_YearBuilt0.022430.14717

结果解释

可以看到，KS 统计量越大，p 值越小。

  • KS Statistic（KS 统计量）：表示样本的经验分布函数与参考分布（如正态分布）的累积分布函数之间的最大差异。数值越小，说明样本分布越接近正态分布。

  • P-Value（p 值）：表示在零假设成立的前提下，观察到当前检验结果的概率。较低的 p 值（通常 < 0.05）意味着应拒绝零假设，说明样本分布与正态分布存在显著差异。

对 “SalePrice” 进行 Quantile 变换 得到了最优结果：KS=0.00719，p=0.99924，说明经变换后数据分布与正态分布高度吻合。这并不意外，因为 Quantile 变换本身就是为实现良好拟合而设计的。p 值接近 1 表明无法拒绝零假设，即数据与正态分布十分接近，正态性良好。

其他变换（如 Log、Box-Cox、Yeo-Johnson）同样改善了 “SalePrice” 的分布，但效果略逊，从较低的 p 值（0.00014–0.00017）可见，说明相比 Quantile 变换，它们与正态分布的吻合程度较低。

对于 “YearBuilt”，变换的整体正态化效果较弱。Box-Cox 和 Yeo-Johnson 相比平方和立方变换略有提升，KS 统计量和 p 值稍低，但仍与正态分布存在显著差异。

“YearBuilt” 的 Quantile 变换结果较好（KS=0.02243，p=0.14717），表明正态性有一定改善，但未达到 “SalePrice” 那样的显著效果。

如何选择合适的变换

选择应对数据偏度的合适变换方法并非“一刀切”，而需要结合数据特征与分析背景进行综合判断。以下是关键考虑因素：

1.数据特征：数据中若存在零或负值，会限制某些变换（如 Log）直接使用。

2.偏度程度：偏度越大，所需变换越强（如 Box-Cox 或 Yeo-Johnson）；轻度偏度可用 Log 或平方根变换处理。

3.统计特性：理想的变换应改善数据的统计性质，如使分布正态化并稳定方差，这对多数统计检验和模型非常重要。

4.可解释性：变换后的结果应易于解释。Log 和平方根变换解释直观，而 Quantile 变换会改变原始数据的尺度结构，解释更复杂。

5.分析目标：分析目的（如预测建模、假设检验或探索分析）直接影响变换选择，应与后续使用的模型或统计方法保持一致。

选择最合适的变换方法取决于多重因素，包括对数据集的充分理解、分析目标，以及模型的可解释性与性能需求。没有任何一种方法在所有情况下都最优，每种变换都有其权衡与适用场景。

需要特别注意的是，Quantile 变换虽在正态化方面效果突出，但属于非线性变换。它可能显著改变数据结构，难以逆向还原原始值，从而影响结果解释或逆变换的可行性。

因此，尽管 Quantile 变换非常强大，但在需要保持原始尺度含义或关注模型可解释性时，应谨慎使用。

在大多数情况下，更推荐选择在“正态化效果”和“可逆性”之间取得平衡的变换，如 Log 或 Yeo-Johnson，以确保数据既规范又可解释。

总结

本文深入探讨了数据变换在处理偏态分布中的重要作用，并通过 Ames 房价数据集中的 “SalePrice” 与 “YearBuilt” 特征，演示了对数、平方根、Box-Cox、Yeo-Johnson、Quantile 等方法的实际效果。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

秋说

感谢打赏

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值