本文介绍了Java中的优先级队列PriorityQueue及其底层数据结构——堆。优先级队列支持插入元素和删除最高优先级元素的操作。堆是一种完全二叉树，分为最大堆和最小堆。在Java中，PriorityQueue的实现基于堆，插入和删除操作遵循堆的性质。文章详细讲解了堆的创建、调整和优先级队列的遍历、异常处理以及扩容策略。
1. 优先级队列的定义
1.1 什么是优先级队列？
优先级队列是由一组元素组成的集合，每个元素都有一个相关的优先级，优先级高的元素先出队列。
具体来说，一个优先级队列应该支持以下操作：
- 插入元素：将一个新元素插入到队列中，并指定它的优先级。
- 删除最高优先级元素：从队列中删除具有最高优先级的元素，并返回它的值。
在优先级队列中，元素的优先级决定了它们在队列中的顺序，在删除最高优先级元素后，要确保队列中剩余元素按照优先级排序。
JDK1.8中的PriorityQueue(Java中的优先级队列)底层使用了堆这个数据结构，堆就是在完全二叉树的基础之上进行了一些元素的调整。
2. 堆
2.1 什么是堆？
堆是一种完全二叉树，其中每个节点的值都不小于（或不大于）其子节点的值。堆分为两种类型：
- 最大堆(大根堆)：对于每个节点，其值都大于或等于其子节点的值。
- 最小堆(小根堆)：对于每个节点，其值都小于或等于其子节点的值。
2.2 堆的存储方式
堆是一棵完全二叉树，因此可以按层序序列的方式用数组来存储，这样比较高效。而非完全二叉树就不适用数组来存储：
完全二叉树能充分地利用空间。
重要性质：
iii 表示数组的下标，nnn 表示树的总节点数：
- i=0i = 0i=0 时，iii 位置的节点为根节点；当 i≠0i \ne 0i=0 时，iii 节点的双亲节点(父节点)的下标为 (i−1)/2(i-1)/2(i−1)/2 。
- 2i+1<n2i+1 < n2i+1<n 时，2i+12i+12i+1 就是它的左孩子下标；2i+1≥n2i+1 \ge n2i+1≥n 时，iii 节点没有左孩子。
- 2i+2<n2i+2 < n2i+2<n 时，2i+22i+22i+2 就是它的右孩子下标；2i+2≥n2i+2 \ge n2i+2≥n 时，iii 节点没有右孩子。
这些性质非常重要，请大家熟记。
2.3 堆的创建
我们已经熟悉了堆的一些性质，那么我们就开始来创建一个堆，由于堆是一棵：每个节点的值都不小于（或不大于）其子节点的值完全二叉树，所以要想创建一个堆，我们就得把一个序列(完全二叉树)调整为前面性质的完全二叉树。
2.3.1 堆的向下调整
给定一棵完全二叉树：{27,15,19,18,28,34,65,49,25,37}，现在要求调整为一个大根堆(每个节点的值都大于子节点的值)。
（注意：把一棵完全二叉树调整为大根堆或小根堆 都是用向下调整法，这里以大根堆为例）
原图：
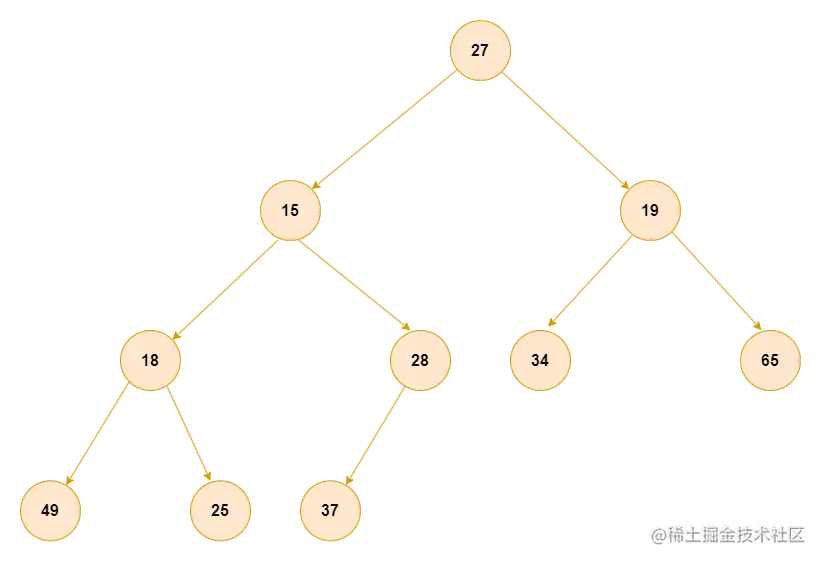
怎么调整？
- 首先我们得从树的最后一个节点开始向下调整，相当于从数组的最后一个元素往前遍历；
- 当前节点是否有孩子节点，没有则往前走；如果有，则把以当前节点为根节点的子树调整为一个堆：
- 比较当前节点和其两个子节点的大小，找到其中最大(或最小)的节点，将当前节点和最大(或最小)的子节点交换位置，并递归地对被交换的子节点进行向下调整(也可以不用递归)，直到当前节点已经成为最大或最小的节点为止。
- 如果根节点本来就最大，往前走。
- 遍历完数组后，调整结束。
动图：
我们来模拟实现堆。
建堆：
public class MyHeap {
public int[] data;
public int usedSize;//有效的数据个数
public MyHeap(){
data = new int[10];
}
//通过传递数组的方式初始化data
public void initData(int[] arr){
this.data = Arrays.copyOf(arr,arr.length);
usedSize = arr.length;
}
//打印这个堆
public void print(){
for (int i = 0; i < usedSize; i++) {
System.out.print(data[i] + " ");
}
System.out.println();
}
//建堆
public void createHeap(int[] arr){
initData(arr);
//parent = (usedSize - 1 -1) / 2 表示最后一个有孩子的节点，直接定位到那去，这里省略了叶子节点。
for (int parent = (usedSize - 1 -1) / 2; parent >= 0; parent--) {
//当前子树进行向下调整为堆
shiftDown(parent,usedSize);
}
}
//将当前的树向下调整为堆
private void shiftDown(int parent,int n){
int maxChild = parent * 2 + 1;//maxChild 为最大的孩子节点，默认是左孩子。
while (maxChild < n){
//判断左右孩子谁大(前提是右孩子存在)
if(maxChild + 1 < n && data[maxChild] < data[maxChild + 1]){
maxChild++;
}
//判断父亲与孩子谁大
if(data[parent] < data[maxChild]){
swap(parent,maxChild);//交换
//向下移动
parent = maxChild;
maxChild = parent * 2 + 1;
} else {
break;//这里为什么是 break? 当父亲 >= 孩子的时候，这棵树已经是堆了(孩子的子树必然是堆，我们是从后往前调的)。
}
}
}
private void swap(int x,int y){
int tmp = data[x];
data[x] = data[y];
data[y] = tmp;
}
}
复制代码测试：
public static void main(String[] args) {
MyHeap myHeap = new MyHeap();
int[] arr = {27,15,19,18,28,34,65,49,25,37};
myHeap.createHeap(arr);
myHeap.print();
}
复制代码结果：
可以看到创建成功。
问题来了，小根堆怎么创建呢？很简单，就是换一个符号，需要改动的代码就只有shiftDown。
private void shiftDown(int parent,int n){
int minChild = parent * 2 + 1;//minChild 为最小的孩子节点，默认是左孩子。
while (minChild < n){
//变为 >
if(minChild + 1 < n && data[minChild] > data[minChild + 1]){
minChild++;
}
//变为 >
if(data[parent] > data[minChild]){
swap(data,parent,minChild);//交换
//向下移动
parent = minChild;
minChild = parent * 2 + 1;
} else {
break;//这里为什么是 break? 当父亲 <= 孩子的时候，这棵树已经是堆了(孩子的子树必然是堆，我们是从后往前调的)。
}
}
}
复制代码2.3.2 建堆的时间复杂度
建堆的代码是：
//建堆
public void createHeap(int[] arr){
initData(arr);
//parent = (data.length - 1 -1) / 2 表示最后一个有孩子的节点，直接定位到那去，这里省略了叶子节点。
for (int parent = (usedSize - 1 -1) / 2; parent >= 0; parent--) {
//当前子树进行向下调整为堆
shiftDown(parent,usedSize);
}
}
复制代码建堆的复杂度：
假设根节点为第一层：
第一层，202^020 个节点，需要向下移动 h-1 层。
第二层，212^121 个节点，需要向下移动 h-2 层。
……
第h-1层，2h−22^{h-2}2h−2 个节点，需要向下移动 1 层。
移动步数：
T(n)=20∗(h−1)+21(h−2)+...+2h−3∗2+2h−2∗1T(n) = 2^0*(h-1)+2^1(h-2)+...+2^{h-3}*2+2^{h-2}*1T(n)=20∗(h−1)+21(h−2)+...+2h−3∗2+2h−2∗1
用错位相减法得出：
T(n)=2h−1−hT(n) = 2^h-1-hT(n)=2h−1−h，又因为 n=2h−1;h=log2(n+1)n = 2^h - 1;h = log_2{(n+1)}n=2h−1;h=log2(n+1)
所以 T(n)=n−log2(n+1)T(n) = n - log_2{(n+1)}T(n)=n−log2(n+1) -> T(n)≈nT(n) \approx nT(n)≈n
所以建堆的时间复杂度是 O(n)O(n)O(n)
2.5 堆的插入、删除
2.5.1 堆的插入
堆的插入总共需要两个步骤：
- 先将元素放入到最底层。
- 将最后新插入的节点向上调整，直到满足堆的性质。
private void swap(int x,int y){
int tmp = data[x];
data[x] = data[y];
data[y] = tmp;
}
//插入元素
public void offer(int val){
//满了就扩容
if(isFull()){
data = Arrays.copyOf(data,data.length * 2);
}
data[usedSize++] = val;
//调整为堆，向上调整
shiftUp(usedSize - 1);
}
//向上调整
private void shiftUp(int child){
//父亲节点
int parent = (child - 1) / 2;
while(child > 0){
//比较子节点与父节点的大小
if(data[child] > data[parent]){
swap(child,parent);
//向上移动
child = parent;
parent = (child - 1) / 2;
}else {
break;
}
}
}
//判断是否满了
public boolean isFull(){
return usedSize >= data.length;
}
复制代码2.5.2 堆的删除
堆的删除操作只能是删除第一个元素，即堆顶：
- 将堆顶元素与堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整
//判读是否为空
public boolean isEmpty(){
return usedSize == 0;
}
//删除堆顶元素
public void pop(){
if(isEmpty()){
throw new NullPointerException("堆为空");
}
//堆顶元素与堆中最后一个元素交换
swap(0,usedSize - 1);
//将堆中有效数据个数减少一个
usedSize--;
//对堆顶元素进行向下调整
shiftDown(0,usedSize);
}
//以 parent 为根节点的树向下调整为堆
private void shiftDown(int parent,int n){
int maxChild = parent * 2 + 1;//maxChild 为最大的孩子节点，默认是左孩子。
while (maxChild < n){
//判断左右孩子谁大(前提是右孩子存在)
if(maxChild + 1 < n && data[maxChild] < data[maxChild + 1]){
maxChild++;
}
//判断父亲与孩子谁大
if(data[parent] < data[maxChild]){
swap(parent,maxChild);//交换
//向下移动
parent = maxChild;
maxChild = parent * 2 + 1;
} else {
break;//这里为什么是 break? 当父亲 >= 孩子的时候，这棵树已经是堆了(孩子的子树必然是堆，我们是从后往前调的)。
}
}
}
复制代码3. 优先级队列
用堆实现优先级队列，其实就是我们上面的代码，上面代码最核心的就是向上调整与向下调整。
3.1 PriorityQueue
在 Java 中，优先队列（Priority Queue）是一个实现了 Queue 接口的类，它可以按照元素的优先级进行排序，每次出队操作都会返回当前队列中优先级最高的元素。Priority Queue 的实现基于堆（Heap）数据结构，使用小根堆（Min Heap）或大根堆（Max Heap）来维护元素的优先级顺序。
它的构造方法：
| 构造方法 | 描述 |
|---|---|
PriorityQueue() | 创建一个具有默认初始容量为11和自然顺序的优先队列。 |
PriorityQueue(Comparator<? super E> comparator) | 创建具有指定比较器的优先队列。 |
PriorityQueue(int initialCapacity) | 创建具有指定初始容量和自然排序的优先队列。 |
PriorityQueue(int initialCapacity, Comparator<? super E> comparator) | 创建具有指定初始容量和指定比较器的优先队列。 |
PriorityQueue(Collection<? extends E> c) | 用一个集合来创建优先级队列 |
PriorityQueue(PriorityQueue<? extends E> c) | 创建具有指定优先队列的副本。使用与指定优先队列相同的比较器，并具有相同的元素。 |
public class Main {
public static void main(String[] args) {
//1.不提供比较器，默认为小根堆
PriorityQueue<Integer> queue1 = new PriorityQueue<>();
//2.提供比较器（匿名内部类），此时为大根堆
PriorityQueue<Integer> queue2 = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
//3.用集合的方式
List<Integer> list = new ArrayList<>();
list.add(1);
list.add(2);
list.add(3);
list.add(4);
PriorityQueue<Integer> queue3 = new PriorityQueue<>(list);
//4.创建具有指定优先队列的副本。
PriorityQueue<Integer> queue4 = new PriorityQueue<>(queue3);
}
}
复制代码| 函数名 | 功能介绍 |
|---|---|
boolean offer(E e) | 插入元素e，插入成功返回true，如果e对象为空，抛出NullPointerException异常，空间不够时候会进行扩容 |
E peek() | 获取优先级最高的元素，如果优先级队列为空，返回null |
E poll() | 移除优先级最高的元素并返回，如果优先级队列为空，返回null |
int size() | 获取有效元素的个数 |
void clear() | 清空 |
boolean isEmpty() | 检测优先级队列是否为空，空返回true |
boolean contains(Object o) | 如果此优先队列包含指定元素，则返回 true。 |
(1). 遍历
可以用for-each来遍历
public static void main(String[] args) {
//提供比较器（匿名内部类），此时为大根堆
PriorityQueue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
queue.offer(1);
queue.offer(10);
queue.offer(20);
queue.offer(30);
queue.offer(40);
queue.offer(50);
queue.offer(60);
for (Integer x: queue) {
System.out.print(x + " ");
}
}
复制代码结果：
迭代器：
public static void main(String[] args) {
//提供比较器（匿名内部类），此时为大根堆
PriorityQueue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
queue.offer(1);
queue.offer(10);
queue.offer(20);
queue.offer(30);
queue.offer(40);
queue.offer(50);
queue.offer(60);
Iterator<Integer> iterator = queue.iterator();
while (iterator.hasNext()) {
System.out.print(iterator.next()+" ");
}
}
复制代码
(2). PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出
ClassCastException异常。
class Student{
int age;
String name;
public Student() {
}
public Student(int age, String name) {
this.age = age;
this.name = name;
}
@Override
public String toString() {
return "Student{" +
"age=" + age +
", name='" + name + ''' +
'}';
}
}
复制代码public static void main(String[] args) {
PriorityQueue<Student> queue = new PriorityQueue<>();
queue.offer(new Student(10,"小明"));
queue.offer(new Student(20,"小明"));
queue.offer(new Student(25,"小明"));
queue.offer(new Student(29,"小明"));
queue.offer(new Student(30,"小明"));
for(Student s:queue){
System.out.println(s);
}
}
复制代码结果：
解决方案：
- Student实现Comparable接口，重写compareTo方法：
class Student implements Comparable<Student>{
.......
.......
@Override
public int compareTo(Student o) {
return this.age - o.age;
}
}
复制代码- 对
PriorityQueue注入比较器：
public static void main(String[] args) {
PriorityQueue<Student> queue = new PriorityQueue<>(new Comparator<Student>() {
@Override
public int compare(Student o1, Student o2) {
return o1.age - o2.age;
}
});
......
......
}
复制代码(3). PriorityQueue 的扩容方式
oldCapacity 表示数组的旧容量。
- 默认初始容量为 11。
- 如果容量小于64时，是按照 oldCapacity 的2倍方式扩容的。
- 如果容量大于等于64，是按照 oldCapacity 的1.5倍方式扩容的。
- 如果容量超过 MAX_ARRAY_SIZE，按照 MAX_ARRAY_SIZE 来进行扩容。
扫一扫
3879
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
