一、实验任务
(1)古希腊的数学发展到亚历山大里亚时期,数学的应用得到了很大的发展,其突出的一点就是三角术的发展,在解三角形的过程中,其中一个比较难的问题是如何利用三角形的三边直接求出三角形面积。这个公式是由古希腊数学家阿基米德得出的,但人们常常以古希腊的数学家海伦命名这个公式,称此公式为海伦公式,因为这个公式最早出现在海伦的著作《测地术》中,并在海伦的著作《测量仪器》和《度量数》中给出证明。
海伦公式:边长分别为a、b、c的三角形的面积S可由以下公式求得
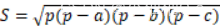
其中p为半周长(周长的一半),即
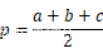
中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”,虽然它与海伦公式形式上有所不同,但它完全与海伦公式等价,它填补了中国数学史中的一个空白,提出的公式为其著作《数书九章》卷五第二题即三斜求积。“问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里,里法三百步,欲知为田几何?”答曰:“三百十五顷.”其术文是:“以小斜幂并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之为实,……开平方得积。”若以大斜记为a,中记为b,小斜记为c,秦九韶的方法即相当于海伦公式
编写求若干个三角形面积的程序,要求由用户交互式输入三角形的边长,判断三边是否构成三角形,在构成三角形的条件下用海伦公式求出三角形的面积,格式化输出如“三角形的三边长为*、*、的三角形面积是”,并能让用户自己决定随时结束求三角形面积。
(2)编写程序,实现图的字典嵌套表示,每个顶点用一个字典表示。如下图中O点表示为:{‘O’: {‘A’:2,‘B’:5,C:4}},其中表示一个顶点和该顶点相连的边及长度,要求输出整个图的顶点数num_vertices、边的个数num_edges以及边的总长度len_edges。
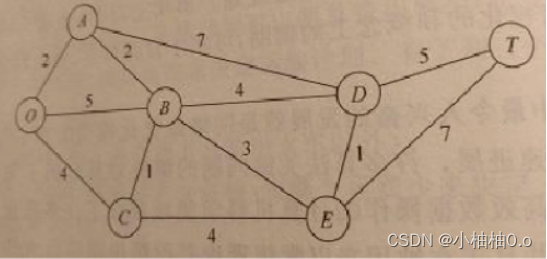
二、实验设计及结果
实验1:
编写求若干个三角形面积的程序,要求由用户交互式输入三角形的边长,
判断三边是否构成三角形,在构成三角形的条件下用海伦公式求出三角形的面积, 格式化输出如“三角形的三边长为*、*、的三角形面积是”,并能让用户自己决定随时结束求三角形面积。
#导入math函数
import math
while True:
# 交互式输入三角形的边长a,b,c,
a = int(input("请输入边长a:")) # eval将字符串当成有效的表达式
b = int(input("请输入边长b:"))
c = int(input("请输入边长c:"))
p = (a + b + c) / 2 # 半周长
# 判断是否构成一个三角形
m = (a + b > c and a + c > b and b + c > a)
if m:
p = (a + b + c) / 2 # 半周长
s = math.sqrt(p * (p - a) * (p - b) * (p - c)) # 面积
print(f"三角形的三边长为{a},{b},{c}的三角形面积是%0.1f" % s) # 0.1f为小数点后一位
else :
print("该三角形不成立,请重新输入")
continue
#退出程序
exit=input("如果你想退出求三角形面积,请输入exit退出程序\n")
if exit == "exit":
print("已退出程序")
break #结束while True无限循环
运行结果:

实验2:
编写程序,实现图的字典嵌套表示,
每个顶点用一个字典表示。如下图中O点表示为:{‘O’: {‘A’:2,‘B’:5,C:4}},
其中表示一个顶点和该顶点相连的边及长度,
要求输出整个图的顶点数num_vertices、边的个数num_edges以及边的总长度len_edges。
顶点数等于所输入的num_vertices;
边数num_edges等于字典中字母的个数;
边的总长度len_edges等于所有数字之和
图的表示:
{‘o’:{‘a’:2,‘b’:5,‘c’:4}}
{‘a’:{‘b’:2,‘d’:7}}
{‘b’:{‘c’:1,‘e’:3,‘d’:4}}
{‘c’:{‘e’:4}}
{‘d’:{‘e’:1,‘t’:5}}
{‘e’:{‘t’:7}}
{‘t’:{}}
#整个图的顶点数num_vertices
num_vertices = int(input("请输入顶点数:"))
#定义边的个数num_edges以及边的总长度len_edges
num_edges = 0
len_edges = 0
print("请输入图的字典的嵌套:")
#for循环取出字典内容
for i in range(num_vertices):
# 图的字典的输入,dict内有{'O': {'A':2,'B':5,C:4}}
# 每行输入表示一个顶点和该顶点相连的边及长度
dict = eval(input()) # eval将str类型转换为int类型
#一个顶点对应的边,取出value值,{'A':2,'B':5,C:4}
for j in dict:
#{'A':2,'B':5,C:4},将key,value赋值在temp,构成新的文件
temp = dict [j]
#定义边的长度为value
for value in temp:
num_edges += 1 #边的个数
len_edges += temp[value] #边的长度
print(f"整个图的顶点数{num_vertices}、边的个数{num_edges}以及边的总长度{len_edges}")
运行结果:
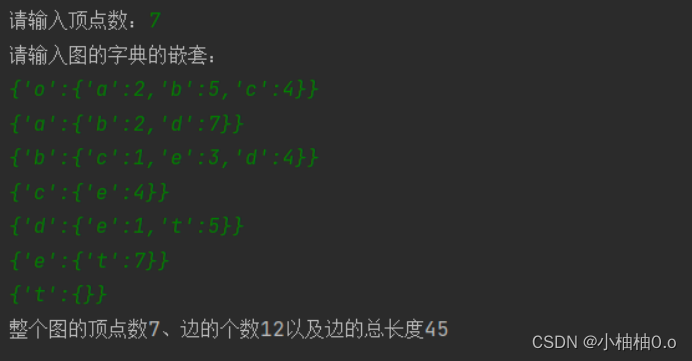





 本文介绍了古希腊时期的三角术发展,特别是海伦公式,以及宋代秦九韶的三斜求积术。还展示了如何编写交互式程序计算三角形面积并实现图的字典嵌套表示。
本文介绍了古希腊时期的三角术发展,特别是海伦公式,以及宋代秦九韶的三斜求积术。还展示了如何编写交互式程序计算三角形面积并实现图的字典嵌套表示。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








